Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

La aceleración es una cantidad física vectorial, que expresa la variación del vector velocidad de cuerpo con respecto al tiempo. La dimensión para expresar la aceleración es longitud dividida entre el tiempo al cuadrado [L]/[T]², es decir, que, en el Sistema Internacional de Unidades, la aceleración sería en metros sobre segundos al cuadrado (m/s²).

En otro orden de ideas, la Segunda Ley de Newton (\(\vec F = m \cdot \vec a\)), establece que la aceleración es directamente proporcional a la fuerza aplicada e inversamente proporcional a la masa del cuerpo. Al despejar de esta expresión a la aceleración, se tiene:

\(\vec a = \frac{{\vec F}}{m}\)

Para que un cohete pueda abandonar la Tierra, debe aplicar una fuerza de propulsión que contrarreste la aceleración del campo gravitatorio y lo impulse al espacio.

Aceleración media (\({\vec a_m}\))

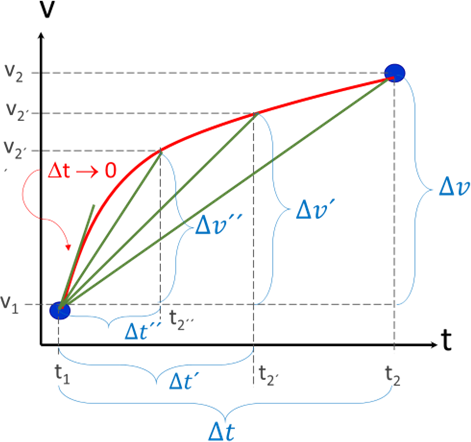
El gráfico muestra la variación instantánea de la velocidad de una partícula respecto al tiempo. La aceleración media se obtiene al dividir el cambio de velocidad entre el intervalo de tiempo en que ocurre dicha variación.

Si consideramos para un cuerpo determinado un gráfico que muestra el cambio de su velocidad con respecto al tiempo (línea roja), se puede determinar la aceleración media del objeto en un intervalo de tiempo. Para ello, se divide el cambio de velocidad entre dicho intervalo de tiempo como se indica en la siguiente expresión:

Esto quiere decir que gráficamente, la aceleración media representa la pendiente de la recta que une a los puntos extremos del intervalo (recta verde) en una gráfica de velocidad – tiempo, y no depende de las velocidades de la partícula en el resto de los instantes que conforman el intervalo de estudio.

Así por ejemplo, si se tiene un vehículo que se desplaza por una carretera horizontal (\(\hat i\)), se sabe además que al inicio del estudio (ti = 0) tiene una velocidad de 30 km/h (vi) y al cabo de 1 hora (tf) adquiere una velocidad de 80 km/h (vf), su aceleración media será:

\({\vec a_m} = \frac{{\left( {80\hat i – 30\hat i} \right)km/h}}{{1\;h – 0h}} = 50\;\frac{{km}}{{{h^2}}}\)

Aceleración instantánea (\(\vec a\))

Si para el gráfico anterior se determina la aceleración media para diferentes periodos de tiempo cada vez más pequeños, se observa que cuando dicho intervalo de tiempo tiende a cero, la recta que une a los puntos de extremos se aproxima a una recta tangente a la curva. Lo anterior implica que matemáticamente, la aceleración instantánea se determina evaluando el límite cuando el intervalo de tiempo t tiende a cero, y esta expresión se transforma a su vez en la derivada de la velocidad con respecto al tiempo:

Como se observa en el gráfico de velocidad – tiempo, a medida que el intervalo de tiempo se reduce hasta un diferencial, la recta que une a los puntos del intervalo se aproxima a la recta tangente a la curva, y esto corresponde al concepto de derivada.

Por ejemplo, si se desea determinar la aceleración de una partícula a los 3 segundos, conociendo que su ecuación de velocidad unidimensional es v = 4t2 – 8, se debe derivar la expresión de la velocidad con respecto al tiempo, lo cual da como resultado:

\(a = \frac{{dv}}{{dt}} = \frac{{d\left( {4{t^2} – 8} \right)}}{{dt}} = 8t\)

Luego, al evaluar la ecuación resultante de la aceleración a los 3 segundos se obtiene:

\(a = 8\left( 3 \right) = 24\frac{m}{{{s^2}}}\)

De aquí se concluye que a los 3 segundos, la velocidad de la partícula se incrementa en 24 m/s por cada segundo.

Aceleración tangencial y centrípeta

La aceleración es una cantidad vectorial, por lo tanto, posee magnitud, dirección y sentido, y se puede expresar a partir de sus componentes.

En el caso del movimiento curvilíneo en dos dimensiones, se suele descomponer a la aceleración de la partícula en dos componentes: una centrípeta y otra tangencial. Cada una de estas componentes está asociada a algún elemento del vector aceleración.

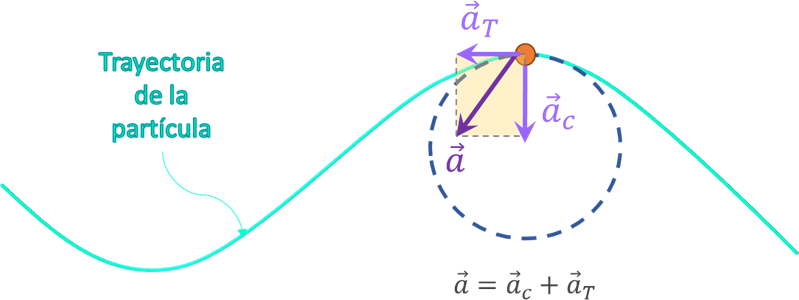
Componentes de la aceleración en el movimiento curvilíneo

La aceleración centrípera (\({\vec a_c}\)): también conocida como aceleración central o normal, es la responsable en el cambio de la dirección del vector aceleración, es decir, está presente en todo movimiento curvilíneo. La dirección de la aceleración centrípeta siempre apunta hacia el centro de la concavidad, y su magnitud se determina con la expresión:

\({a_c} = \frac{{{v^2}}}{r}\)

Donde:

v: módulo de la velocidad de la partícula

r: radio del círculo inscrito en la curvatura

La aceleración tangencial (\({\vec a_T}\)): esta componente está relacionada con el cambio en la magnitud de la velocidad de la partícula. Solo está presenta cuando la velocidad de la partícula cambia de módulo (acelera o desacelera). Su dirección siempre es tangente a la circunferencia inscrita en un punto específico de la trayectoria de la partícula, y su magnitud es:

\({a_T} = \alpha .r\)

Donde:

α: aceleración angular (rad/tiempo2)

\(\alpha = \frac{{d\omega }}{{dt}}\)

r: radio del círculo inscrito en la curvatura

ω: velocidad angular de la partícula (rad/tiempo)

La magnitud de la aceleración total se determina a partir de la suma vectorial de las componentes centrípeta y tangencial:

\(\vec a = {\vec a_c} + {\vec a_T}\)

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

Art. actualizado: Oct. 2022; sobre el original de septiembre, 2010.

Datos para citar en modelo APA: Marín, E. M. (Oct. 2022). Definición de Aceleración. Significado.com. Desde https://significado.com/aceleracion/