¿Qué es el Alfa de Cronbach y cómo se define?

Marcoantonio Villanueva Bustamante
Doctor en Psicología

El alfa de Cronbach es el coeficiente más usado para estimar la consistencia interna de una escala de medición.

Uno de los elementos fundamentales al construir y usar una escala es la fiabilidad, esta es definida como la estabilidad que presenta un instrumento de medición, cuando se aplica en múltiples ocasiones mientras se presenten condiciones similares. Dicho de otra forma, la fiabilidad indica que tan preciso es un instrumento de medición evaluando el constructo de interés en más de una ocasión. Para evaluar la fiabilidad, se puede recurrir a múltiples técnicas, como el coeficiente test-retest que establece la correlación entre la respuesta de un instrumento de medición que se aplica en dos ocasiones distintas; el coeficiente de formas paralelas, se calcula mediante la aplicación de un instrumento que posee dos versiones distintas; finalmente, el coeficiente de consistencia interna que no requiere más de una medición, este coeficiente puede ser calculado mediante diversos métodos, pero el Alfa de Cronbach, es el más común.

El alfa de Cronbach es propuesta por Lee J. Cronbach en el 1951, como una medida ante la limitación del coeficiente KR-20 y KR-21 desarrollados por Kuder y Richardson, los cuales sólo pueden ser aplicado en escalas que cuentan con opciones de respuesta dicotómicas.

Para calcular el alfa de Cronbach (α), se recurre a la siguiente fórmula:

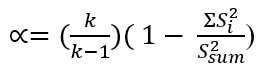
Donde k es el número ítems de la prueba; S_i² es la varianza de los ítems y S_sum² es la varianza total de la escala. Dicho de otra forma, al alfa se obtiene mediante el cálculo de la correlación de cada reactivo de la escala con cada uno de los otros reactivos, posteriormente se promedian estas correlaciones y el resultado sería el valor de alfa, cabe mencionar que estas correlaciones se estiman mediante el coeficiente de correlación de Pearson. Por lo tanto, la fiabilidad mediante el alfa se relaciona con la longitud de la escala y el nivel de covarianza (correlación) entre sus ítems. El valor de alfa de Cronbach puede encontrarse entre 0 y 1, entre más cercano al 1 representa mejor índice de consistencia interna; en este sentido, el valor mínimo aceptable de alfa es de .70 y valores superiores a .90 indicarían redundancia en los ítems.

El alfa de Cronbach se ha convertido en el método más usado para estimar la consistencia interna de una escala, debido a sus ventajas por sobre otros métodos, pero también debido a que la mayoría de los paquetes y programas estadísticos pueden estimar este valor. Sin embargo, el uso del alfa de Cronbach no está exento de críticas, la mayoría de estas surgen a raíz de la violación de sus supuestos.

Supuestos del Alfa de Cronbach

1. Equivalencia Tau, esta se refieren a que todos los ítems de una escala midan el mismo rasgo o el mismo factor latente con grado de precisión similar.
2. Los errores no deben estar correlacionados, pues se asume que estos son independientes.
3. Unidimensionalidad de los ítems, es decir, los ítems de una escala deben medir un solo rasgo latente.
4. El nivel de medición de la variable operacionalizada debe ser continua.

El incumplimiento de cualquiera de estos supuestos puede ocasionar una estimación errónea en los valores del Alfa de Cronbach. Sin embargo, dado la naturaleza de los datos en ciencias sociales y de la salud es habitual no cumplir el cuarto supuesto; es decir, los datos tienden a ser ordinales. Aplicar el coeficiente de alfa a datos ordinales, especialmente cuando se tiene menos de 5 opciones de respuesta, puede ocasionar un subestimación de los valores. Por tal motivo, han surgido alternativas para al Alfa de Cronbach.

El alfa Ordinal

La estimación de la consistencia interna mediante el alfa ordinal sigue la misma lógica que el Alfa de Cronbach, con la diferencia, que en vez de usar la matriz de correlación de Pearson, alfa ordinal utiliza la matriz de correlación policórica o tetracórica. Del mismo modo, a diferencia del alfa de Cronbach que es sensible a la asimetría de los datos, alfa ordinal es un estimados insesgado.

Omega de McDonald

Ante el incumplimiento del supuesto de la equivalencia entre los ítems, el omega de McDonald es un método de estimación de la consistencia interna que ha ido ganando relevancia. Entre las ventajas de este coeficiente se encuentran que a diferencia del alfa, omega trabaja con las cargas factoriales de cada reactivo y no depende del número de ítems de la escala, tal cómo puede observarse en la siguiente fórmula.

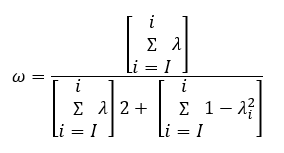
Donde λ es la carga factorial y λ_i es la carga factorial, estandarizada. De manera similar a alfa de Cronbach, valores de omega entre .70 y .90 representan valores adecuados.

Pese a las ventajas que representan el uso de alfa ordinal y omega de McDonald su aplicación en la investigación aún es escasa, es posible que esto se deba a que la mayoría de los paquetes y softwares estadísticos aun no cuentan con una opción para estimarlos.

Por: Marcoantonio Villanueva Bustamante. Licenciado en Psicología, egresado de la Facultad de Psicología de la UNAM, México. Doctor en Psicología por la UFRO, Chile. Actualmente, es investigador independiente que forma parte de diversos equipos de investigación en México y Chile.

Trabajo publicado en: Ene., 2023.

Datos para citar en modelo APA: Villanueva Bustamante, M. (enero, 2023). Definición de Alfa de Cronbach. Significado.com. Desde https://significado.com/alfa-cronbach/