Significado de análisis de Fourier (series y transformada) Definición, y explicación

Doctor en Ingeniería
Definición formal
El Análisis de Fourier aborda la aproximación de funciones mediante la suma de funciones trigonométricas simples. Este tipo de representaciones resulta sumamente útil en diversas aplicaciones, que incluyen resolución de ecuaciones en derivadas parciales, procesamiento de señales e imágenes, teoría de Probabilidad, etc.
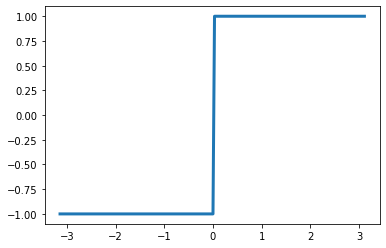
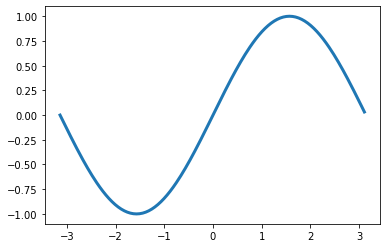
¿Pero qué alcance tienen estas aproximaciones? ¿Qué pasaría si quisiéramos, por ejemplo, aproximar una función escalonada? En la figura 1 vemos que, mientras la función es constante por partes y presenta discontinuidades, en la figura 2, la función seno de que disponemos, es suave y continua. No obstante, la importancia del Análisis de Fourier tiene que ver con que todas las funciones integrables con que nos encontramos en la práctica son Fourier-aproximables, y ya veremos cómo.
Explicación de las Series de Fourier
Consideremos una función integrable y periódica \(f:\mathbb{R}\rightarrow\mathbb{R}\), con período T. Entonces, f puede aproximarse, para todo \(t\in\mathbb{R}\), mediante una Serie de Fourier
\(f(t) \approx \frac{a_0}{2} + \sum_{n=1}^\infty\left[a_n\cos\left(\frac{2\pi n}{T}t\right)+b_n\sin\left(\frac{2\pi n}{T}t\right)\right]\)
donde an y bn se denominan coeficientes de Fourier, y pueden calcularse como
\(a_n & = \frac{2}{T}\int_{-T/2}^{T/2}f(t)\cos\left(\frac{2\pi n}{T}t\right) dt\) ,
\(b_n & = \frac{2}{T}\int_{-T/2}^{T/2}f(t)\sin\left(\frac{2\pi n}{T}t\right) dt\)
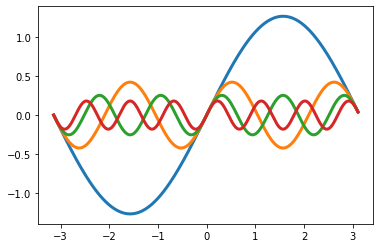
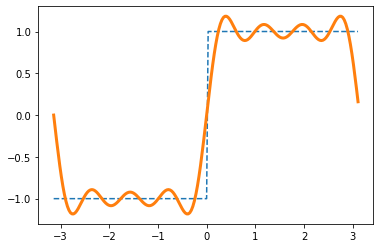
Si utilizamos esta fórmula para calcular los coeficientes de Fourier de la función escalonada de la figura 1, veremos que \(a_n=0 \;\forall n\in\mathbb{N}\), mientras que los coeficientes bn determinan la amplitud de los senos en la gráfica 2, cuya suma de Fourier (utilizando las primeras 4 componentes) puede verse en la representación anterior. Es claro que la aproximación con 4 componentes no es perfecta, pero en la práctica no podemos utilizar infinitos coeficientes, por lo que debemos conformarnos con aproximaciones, que normalmente funcionan muy bien.
Transformada de Fourier
Veamos ahora una generalización de lo anterior a un espacio continuo. Para ello, consideremos una función \(f:\mathbb{R}\rightarrow\mathbb{R}\) integrable. Se define la Transformada de Fourier de f en frecuencia xi como
\(\hat{f}(\xi) \doteq \int_{-\infty}^\infty f(x)e^{-2\pi i x \xi}dx\)
El término \(e^{-2\pi i x \xi}\) no es otra cosa que una generalización de suma de senos y cosenos utilizando la identidad de Euler. La primera propiedad importante de esta transformada es el Teorema de Inversión de Fourier, que en términos simples dice que
\(f(x) = \int_{-\infty}^\infty \hat{f}(\xi)e^{2\pi i x \xi}d\xi\)
Es decir, que la Transformada de Fourier es invertible, y podemos recuperar f de manera exacta a través de su transformada.
La transformada de Fourier tiene muchas aplicaciones, que van desde resolución de ecuaciones diferenciales hasta procesamiento de señales e imágenes. Una de sus propiedades más importantes es el Teorema de Convolución, que establece que dadas dos funciones integrables f y g, cuya convolución se define como
\((f\ast g)(x) \doteq \int_{-\infty}^\infty f(t-x)g(t) dt\) ,
se cumple que
\(\widehat{f\ast g}(\xi) = \hat{f}(\xi)\hat{g}(\xi)\) ,
y por lo tanto podemos calcular \((f\ast g)(x)\) aplicando la transformada inversa de Fourier al producto \(\hat{f}(\xi)\hat{g}(\xi)\), a menudo más sencillo y computacionalmente menos costoso de calcular que utilizando la definición de convolución.
Transformada de Fourier de Tiempo Corto
Existen otras variantes de esta transformada, como ser la Transformada de Fourier de Tiempo Corto (STFT), muy utilizada en procesamiento de audio, que consiste en cortar una sección de una señal utilizando una «ventana», calcular los coeficientes de Fourier, mover la ventana en el tiempo y repetir el proceso, obteniendo un espectrograma, como se ve en la figura 5.
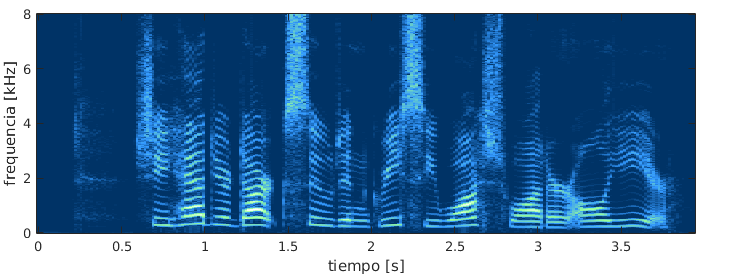
Esta transformada se define a partir de una ventana \(w:\mathbb{R}\rightarrow\mathbb{R}\) de soporte acotado y que cumple \(\int_{-\infty}^\infty w(t)dt = 1\) , que sirve para «cortar» un intervalo temporal. A partir de esto, la STFT se define en el plano como
\(F(\tau, \xi) \doteq \int_{-\infty}^\infty f(x)w(t-\tau)e^{-2\pi i x \xi}dx\) ,
permitiendo un análisis de la función tanto en tiempo \(\tau\) como en frecuencia \(\xi\).

Trabajo publicado en: Jun., 2021.