Significado de autoencoder Definición, encoder y decoder, y variacional

Doctor en Ingeniería
Definición formal
Autoencoder es una clase de Red Neuronal Artificial que permite aprender una representación latente (de dimensión reducida) de los datos de manera no-supervisada. Lo que se busca es que, dado un conjunto de datos, cada elemento quede representado de manera biunívoca por unos pocos parámetros que permitan reconstruirlo, e incluso a veces generar nuevos datos no observados.
Pensemos en una imagen de 100x100px de un círculo negro sobre un fondo blanco. Cada uno de los 10000 píxeles tiene entonces un valor binario (blanco o negro) que determina la imagen. No obstante, si en vez de almacenar el valor de cada uno de los 10000 píxeles, almacenáramos como información el radio del círculo y las coordenadas x e y del centro, podríamos dibujarlo, reproduciéndolo exactamente. Esto es un ejemplo de codificación supervisada, pues yo construyo una regla sobre cómo obtener la información que determina el círculo, y un método para dibujarlo luego a partir de esa información. Un Autoencoder, en cambio, aprende las reglas de compresión y reconstrucción, y desde luego puede utilizarse en tareas mucho más complejas.
Diferencia entre encoder y decoder en el funcionamiento
Un Autoencoder consta de dos redes neuronales en serie:
1. Un Encoder, que mapea la entrada a un espacio latente de menor dimensión.
2. Un Decoder, que mapea una variable del espacio latente hacia una salida.
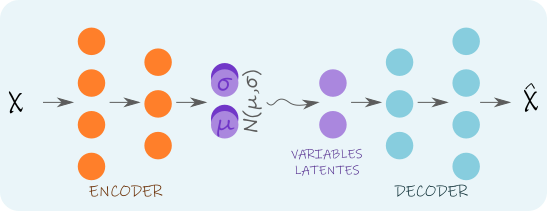
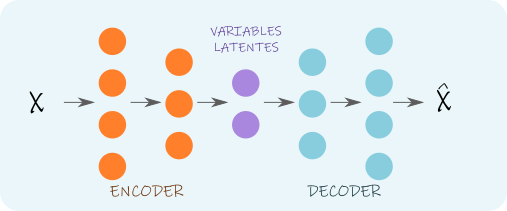
El Encoder típicamente cuenta con varias capas, que disminuyen en tamaño (cantidad de neuronas) a medida que nos acercamos al espacio latente. El Decoder suele definirse como una red neuronal simétrica al Encoder, con capas que crecen en tamaño hacia la salida, que debe aproximar lo mejor posible a la entrada. Dado que la información trata de preservarse a través de ese cuello de botella (Figura 1) que se forma por la arquitectura de la red, se fuerza una compresión de la información, que el Decoder aprende a entender.
Como siempre que hablamos de Redes Neuronales Artificiales, mencionamos un «aprendizaje». Este tipo de redes se entrenan mediante \emph{backpropagation} (un proceso de descenso por gradiente), utilizando una función de costo \(L(\hat{x};x)\), donde x es el dato, y \(\hat{x}\) la salida de la red. Esta función puede definirse como:
\(L(\hat{x};x) \doteq & \|\hat{x}-x\|_2^2\) ,
\(L(\hat{x};x) \doteq & \|\hat{x}-x\|_1\) ,
o alguna otra variante que incluya términos de regularización, según el tipo de datos con que estemos trabajando. La idea es siempre la misma: modificar los parámetros de la red para tratar de minimizar una función de costo en todo el conjunto de datos de entrenamiento.
Según el tipo de información, puede variar el tipo de capas en la red. Por ejemplo, para valores tabulares podemos usar capas completamente conexas (perceptrones), mientras que para imágenes preferiremos utilizar capas convolucionales y para mallas tridimensionales, alguna estructura de grafo.
Autoencoder Variacional
Existe otro tipo de Autoencoders denominados Variacionales, que parten de la misma idea que los anteriores, pero en lugar de comprimir información, su objetivo es típicamente el de generar nuevos datos. Es decir, una vez entrenado el modelo, nos olvidamos del Encoder, y empezamos a cambiar los valores de las variables latentes para usarlos de input en el Decoder y generar nuevos datos.
Mientras que un Autonecoder no-variacional permite compresión de información, no podemos asegurar que cualquier punto del espacio latente producirá un resultado apropiado. Pensemos, por ejemplo, en comprimir imágenes de dígitos escritos. Un Autonecoder no-variacional puede hacer esto, pero si luego quitamos el Encoder y ponemos un valor latente al azar, podríamos obtener en vez de un número una letra, o directamente un garabato.
Para lograr resultados consistentes, un Encoder Variacional produce como salida (en lugar de las variables latentes) los parámetros de una distribución de probabilidad (típicamente Normal) a partir de los cuales se generan valores al azar para darle como entrada al Decoder. De esta forma, los datos no se mapean a puntos sino a distribuciones, por lo que puntos cercanos en el espacio latente corresponden a datos parecidos. Un ejemplo de este uso puede verse en la Figura 3, donde los resultados se muestran en función de dos variables latentes (una que varía horizontalmente, y la otra verticalmente).

Dentro del marco de los Autoencoders Variacionales existen también variantes, que permiten generar muestras condicionadas, regularizadas e incluso hay enfoques multicanal, en los que varios Autoencoders se unene en paralelo.

Trabajo publicado en: Ene., 2021.