Significado de caída libre Definición, ejemplos, y ecuaciones

Licenciada en Física
Definición formal
La caída libre, en carácter ideal, es el movimiento de un cuerpo cercano a la superficie terrestre, liberado a cierta altura respecto al suelo, despreciando el roce con el aire y sin que actúe ninguna otra fuerza, salvo la atracción gravitacional terrestre, supuesta constante.
En principio, la condición de que no exista roce con el aire se cumple solo en el vacío. Y, por otro lado, el hecho de que la atracción gravitacional sea constante supone, en efecto, cercanía con la superficie. Ambas suposiciones simplifican bastante las cosas, y por eso el modelo se llama caída libre ideal, pero describe muy acertadamente el comportamiento de cualquier objeto que se suelta cerca del suelo.
El sabio Galileo Galilei fue el primero en estudiar concienzudamente este movimiento tan frecuente. Se cuenta que Galileo subía muchas veces hasta lo alto de la torre de Pisa, en su ciudad natal, para dejar caer objetos, luego de lo cual concluyó que:

Características del movimiento de caída libre
Los siguientes puntos destacan las principales características de la caída libre en su versión más simple:
• El objeto que cae, llamado también “el móvil”, se libera a cierta altura sobre el suelo, luego, su velocidad inicial es 0.
• La trayectoria que sigue el móvil es una recta vertical.
• La aceleración del móvil es constante, se denota como “g” y siempre, siempre está dirigida verticalmente hacia el suelo. Su magnitud es, con buena aproximación: g = 9.8 m/s2 o g = 32 pies/s2 y el signo depende del sentido que se tome como positivo (hacia arriba o hacia abajo).
• A medida que desciende, el móvil adquiere una rapidez mayor, y el tiempo que tarda en tocar el suelo depende únicamente de la altura desde la cual se soltó. Ambas magnitudes, rapidez y tiempo, son independientes de la masa del objeto, entonces, dos objetos liberados desde la misma altura, llegan al suelo al mismo tiempo.
Para describir el movimiento, incluyendo la caída libre, se requiere un sistema de referencia. En este caso, se supondrá que el móvil se desplaza a lo largo del eje “y”. En cualquier punto, tiene una velocidad vy y la aceleración de la gravedad “g” siempre apunta hacia abajo, como se ilustra en la imagen:
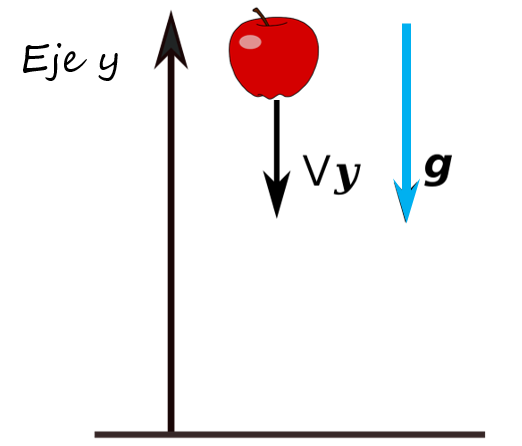
Ejemplos de caída libre
Caída desde el reposo de objetos comunes
La caída de una fruta, que repentinamente se desprende de la rama y llega al suelo, es un buen ejemplo de caída libre. Originalmente la fruta estaba en reposo, y luego la gravedad la acelera hasta el suelo.
La leyenda afirma que Isaac Newton concibió la idea de la gravedad cuando, sentado en el prado bajo un gran manzano, una de estas frutas cayó sobre su cabeza.
No es seguro que en realidad haya sucedido de esta forma, pero es muy probable que ver caer las manzanas, hiciera que Newton, gran observador de la naturaleza, se preguntara acerca de las causas de este movimiento.
Paracaidismo
Si un paracaidista se deja caer desde la portezuela del avión, mientras que el paracaídas aún no se abre, su movimiento es en caída libre.
Pero una vez que el paracaídas se abre, aparece una fuerza salvadora hacia arriba, que contrarresta la gravedad. Entonces el movimiento deja de ser caída libre, lo cual amortigua la caída para que el paracaidista llegue a salvo al suelo.
Ecuaciones
Partiendo de las características antes descritas, las ecuaciones de la caída libre ideal se plantean tomando en cuenta que:
• El punto de partida del movimiento es y = 0 y el sentido positivo se escoge hacia abajo.
• El punto de llegada es y = h, donde “h” es la altura desde donde cae el objeto
• La velocidad inicial es 0
Posición
\(y=\frac{1}{2}g\cdot {{t}^{2}}\)
Velocidad
\(v=g\cdot t\)
Velocidad en función de la posición
\({{v}^{2}}=2g\cdot y\)
Ejercicio práctico e ilustrativo: averiguar la profundidad de un pozo o barranco
Al soltar libremente una piedra o una moneda desde cierta altura, su movimiento es una caída libre como la descrita arriba.
Con la ayuda de un cronómetro y teniendo un fino oído, es posible averiguar la altura de un barranco o la profundidad de un pozo, dejando caer una piedra y midiendo el tiempo que transcurre desde que se suelta, hasta que se escucha el sonido del choque de la piedra contra la superficie o contra el agua.
Después, hay que analizar dos movimientos, en primer lugar, la caída libre de la piedra o moneda y segundo, el movimiento del sonido del choque, cuando viaja desde el fondo hasta el oído de la persona.
Las ecuaciones de la piedra o la moneda son como las descritas arriba, y para el sonido, se supone que este se mueve en línea recta con rapidez constante de vs = 344 m/s aproximadamente.
Nótese que el tiempo que tarda la piedra o moneda en caer, es diferente del que tarda el sonido en subir, este último, desde luego, es más veloz. En cambio, el tiempo que cronometra la persona es la suma de ambos tiempos.
Lo que sí es igual para el sonido y la piedra es la distancia que ambos recorren, que no es otra que la profundidad buscada:
\({{h}_{piedra}}={{h}_{sonido}}\)
\({{t}_{piedra}}+{{t}_{sonido}}={{t}_{cronometrado}}\)
Suponiendo que el tiempo cronometrado es de 2.5 segundos y abreviando piedra con “p”, y sonido con “s”, se tiene:
\({{h}_{p}}={{h}_{s}}\)
\(\frac{1}{2}g{{\left( {{t}_{p}} \right)}^{2}}=344\cdot {{t}_{s}}\)
Con:
\({{t}_{p}}+{{t}_{s}}=2.5\)
\(\frac{1}{2}g{{\left( {{t}_{p}} \right)}^{2}}=344\cdot \left( 2.5-{{t}_{p}} \right)\)
Despejando ts y sustituyendo el despeje en la ecuación que iguala las distancias, más un poco de álgebra sencilla, se logra una ecuación de segundo grado:
\(4.9{{\left( {{t}_{p}} \right)}^{2}}+344{{t}_{p}}-860=0\)
La solución de esta ecuación es el tiempo que tarda la piedra en caer, y conociendo este valor, la profundidad buscada es:
\({{h}_{p}}=\frac{1}{2}g\cdot {{\left( {{t}_{p}} \right)}^{2}}\)
La solución de la ecuación de segundo grado planteada es:
\({{t}_{p}}=2.42~segundos\)
Por lo tanto, la profundidad del pozo o barranco es:
\({{h}_{p}}=\frac{1}{2}9.8\cdot {{\left( 2.42 \right)}^{2}}=28.7~metros\)

Trabajo publicado en: Jun., 2021.