Definición de Centroide

Ingeniera Industrial, MSc en Física, y EdD
El centro de área o centroide de área es un concepto matemático utilizado para determinar el punto medio geométrico de una figura plana, lo que significa que, dada cualquier forma bidimensional como un cuadrado, rectángulo o polígono regular o irregular, se puede encontrar su centroide calculando la media aritmética ponderada del punto en el borde exterior.
El uso principal de este parámetro es ayudar a los ingenieros a diseñar estructuras adecuadas para resistir fuerzas externas y minimizar la cantidad total necesaria materiales empleados en su construcción. Esta técnica se usa ampliamente en la ingeniería, arquitectura y diseño gráfico para calcular la ubicación precisa de los elementos que componen las figuras planas, y puede ser útil a la hora de determinar el peso o centrífugos en estructuras complejas, así como cuando se necesita conocer los momentos y fuerzas internamente equilibrados dentro del sistema mecánico.
Existen varias formas para determinar la ubicación del centro de área de una figura plana. El más general (y que emplean los paquetes informáticos) es mediante integrales, sin embargo, cuando se trata de figuras geométricas de formas regulares, se suele aplicar el método de descomposición de figuras.
Mediante el método de integración, se requiere conocer la ecuación de la curva generatriz que describe el contorno de la figura, ya que el cálculo de una integral representa el área (A) de dicha curva. Luego, las coordenadas del centroide se denotan como (\(\bar x,\;\bar y\)), siendo:
\(\bar x = \frac{{\smallint x \cdot dA}}{A}\)
\(\bar y = \frac{{\smallint y \cdot dA}}{A}\)
Ahora bien, debido a las dificultades matemáticas que se pueden presentar para determinar la curva generatriz, cuando en la práctica se resuelven problemas de centroide de forma manual, se suelen hacer aproximaciones, intentando que el área a analizar, sea la composición (suma y/o resta) de otras áreas regulares.
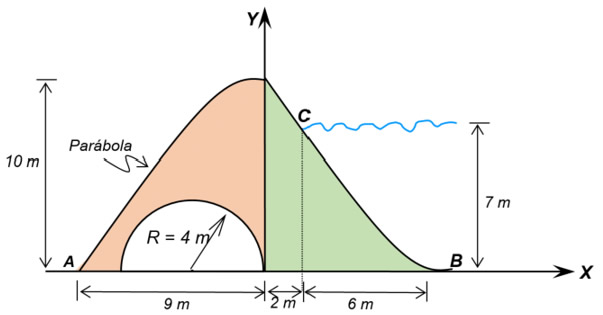
Si suponemos que el área sombreada representa el perfil de un dique que soporta una masa de agua ubicada del lado derecho, el método de figuras compuestas consiste en identificar las áreas que conforman esta figura, en este caso, una semiparábola (color salmón) + una enjuta parabólica (color verde) – un semi-círculo (parte hueca en color blanco).
Algunos criterios para el cálculo del centro de área a tener en cuenta son:
• Si la figura posee un eje de simetría, el centroide se ubica en algún punto sobre dicho eje.
• Si el área presenta dos o más ejes de simetría, el centro de área se localiza en el punto de intersección de estos ejes.
El procedimiento general a seguir en el cálculo del centro de área para figuras compuestas es:
1. En primer lugar, hay que identificar qué figuras geométricas forman parte de la principal figura plana, antes incluso empezar a hacer algún cómputo matemático. Un triángulo equilátero tendría tres ejes de simetría, mientras que un rectángulo solo tiene dos y un círculo posee infinitos ejes de simetría (diametrales).
2. A cada figura se le determina su área y centro de área, y luego se multiplica el área de cada figura por su correspondiente coordenada del centroide en los ejes del plano. La siguiente tabla muestra las fórmulas de área y centroide de algunas figuras planas comunes:
| Figura | Área y Centroide | Figura | Área y Centroide |
|---|---|---|---|
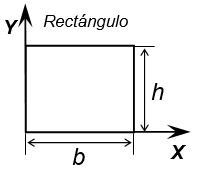 |
\(A = bh\) \(\bar X = \frac{b}{2}\) \(\bar Y = \frac{h}{2}\) |
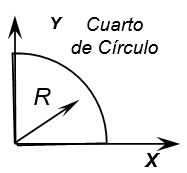 |
\(A = \frac{{\pi {R^2}}}{4}\) \[\bar X = \bar Y = \frac{{4R}}{{3\pi }}\] |
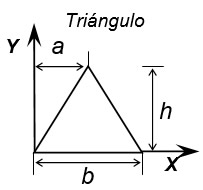 |
\(\bar Y = \frac{h}{3}\) \(\bar Y = \frac{h}{3}\) |
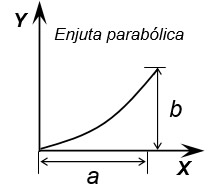 |
\(A = \frac{{ah}}{3}\) \[\bar X = \frac{{3a}}{4}\] \[\bar Y = \frac{{3h}}{{10}}\] |
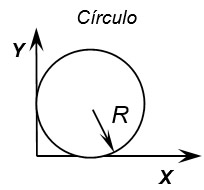 |
\(A = \pi {R^2}\)
\(\bar X = R\) \[\bar Y = R\] |
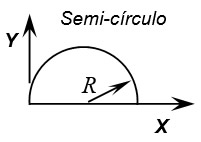 |
\(A = \frac{{\pi {R^2}}}{2}\) \(\bar X = R\) \(\bar Y = \frac{{4R}}{{3\pi }}\) |
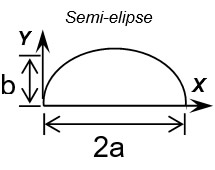 |
\[A = \frac{{\pi \,ab}}{2}\] \(\bar X = a\) \(\bar Y = \frac{{4b}}{{3\pi }}\) |
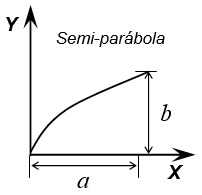 |
\(A = \frac{{2ab}}{3}\) \(\bar X = \frac{{3a}}{5}\) \(\bar Y = \frac{{3b}}{8}\) |
3. Luego, hay que sumar todos los productos de cada área con el centroide, y las coordenadas del centro de área para la figura compuesta (en unidades de longitud), serán:
\(\bar x = \frac{{\sum {{\bar x}_i} \cdot {A_i}}}{A}\)
\(\bar y = \frac{{\sum {{\bar y}_i} \cdot {A_i}}}{A}\)
Finalmente, una vez obtenido el resultado, hay muchas formas de utilizar el cálculo del centro de área para analizar y resolver problemas complejos en ingeniería o diseño gráfico, por lo que sirve como un instrumento poderoso para otros cálculos como el momento y producto de inercia de la figura compuesta.

Una de las aplicaciones del cálculo del centro de área es para la ubicación del centro de masa aproximado para un dique o represa, que soporta la fuerza ejercida por una masa de agua. Este parámetro es indispensable para un diseño adecuado que garantice la estabilidad del mismo.
Herramientas computacionales para el cálculo del centro de área
El procesamiento computacional ha ampliado las capacidades para el cálculo del centro de área, al permitir que los ingenieros creen modelaciones tridimensionales más precisas con menor tiempo invertido en cálculos manuales intensivamente complejos. Con softwares modernos, es posible determinar rutinariamente los valores exactos de áreas y centros geométricos para muchas formas complejas sin ningún tipo de error humano o involuntario.
Aunado al planteamiento anterior, el uso de software permite llevara a cabo análisis estáticos y dinámicos del comportamiento de la estructura y pueden generar gráficos que representan la distribución de presiones y tensiones dentro del objeto y su relación con distintos elementos exteriores alrededor del mismo. Esto es especialmente útil cuando deben diseñarse estructuras robustas y capaces de soportar fuerzas extremas con un mínimo de esfuerzo energético o exigir diseños de algunos tipos específicos o formas tridimensionales que de manera analítica manual resultaría demasiado laboriosa.
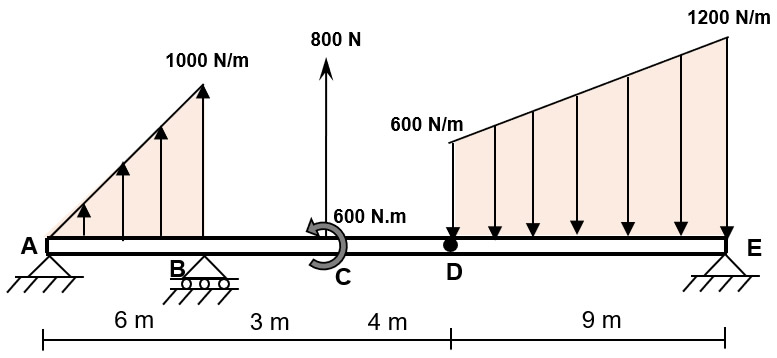
El cálculo del centro de área es fundamental en ingeniería civil, para determinar el punto de aplicación de la fuerza resultante de cargas distribuidas, como en el caso del análisis de vigas.

Trabajo publicado en: Mar., 2023.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.