Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

Cinemática

En Física, la cinemática representa el área de esta ciencia que estudia el movimiento de los cuerpos, sin considerar las causas que lo producen, es decir, se analiza las características y evolución del movimiento a lo largo del tiempo, pero no las razones que lo originaron.

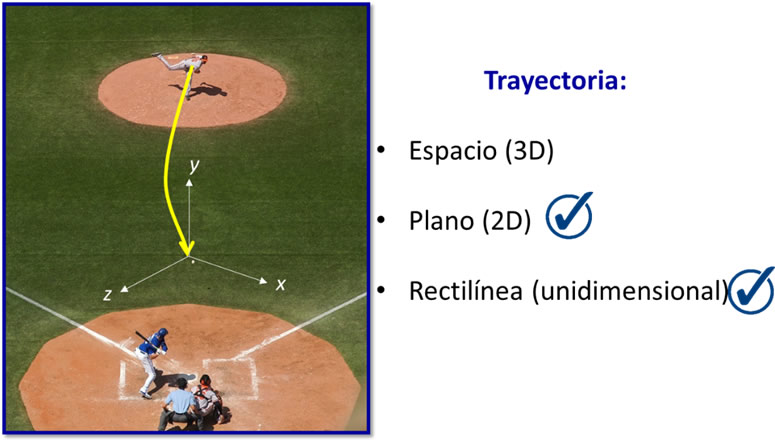
En la mayoría de los cursos de Física mecánica básica, se suele estudiar la cinemática para trayectorias unidimensionales y bidimensionales.

Como en muchas áreas de la física, en cinemática, se suelen tomar ciertas consideraciones a fin de simplificar el estudio de los casos, manteniendo resultados con aproximaciones aceptables a los hallazgos experimentales bajo condiciones similares. Las principales consideraciones a tener en cuenta en cinemática son:

• Los cuerpos se consideran partículas, esto es, puntos geométricos a los que se le asocia una masa. En el caso de cinemática, esta información es relevante ya que el único movimiento asociado a las partículas a nivel macroscópico es el de traslación, por lo tanto se estaría hablando de cinemática de una partícula. Por su parte, el movimiento de rotación, es aplicable para cuerpos con dimensiones y se analiza a través de parámetros como el torque o momento estático.

• Se desprecia la resistencia del aire. Esta premisa es de gran relevancia, principalmente en movimientos donde participa la aceleración de la gravedad, como el movimiento en caída libre o en el movimiento parabólico.

• La aceleración de la gravedad es una cantidad vectorial cuyo módulo, dirección y sentido permanece constante para la situación problemática que se esté analizando; y siempre se considerará vertical hacia abajo, ya que en los espacios que se consideran, la curvatura de la Tierra es imperceptible. Por el contrario, si se toma en cuenta la curvatura de la Tierra y la distancia desde su superficie hasta el centro, la aceleración de la gravedad tiene dirección radial y su magnitud varía.

• En la mayoría de los cursos académicos, se suele suponer el movimiento en una o dos dimensiones, aunque en la práctica, una partícula también puede describir una trayectoria tridimensional.

Tipos de movimiento para una partícula

Como se ha citado, una partícula, al no tener dimensiones, no puede experimentar efecto de rotación, por lo que la única posibilidad de movimiento es el de traslación, que quiere decir, un cambio de posición respecto a un sistema de referencia inercial. Para facilitar el estudio de los principales tipos de movimiento analizados en la cinemática de una partícula, se ha propuesto la siguiente clasificación:

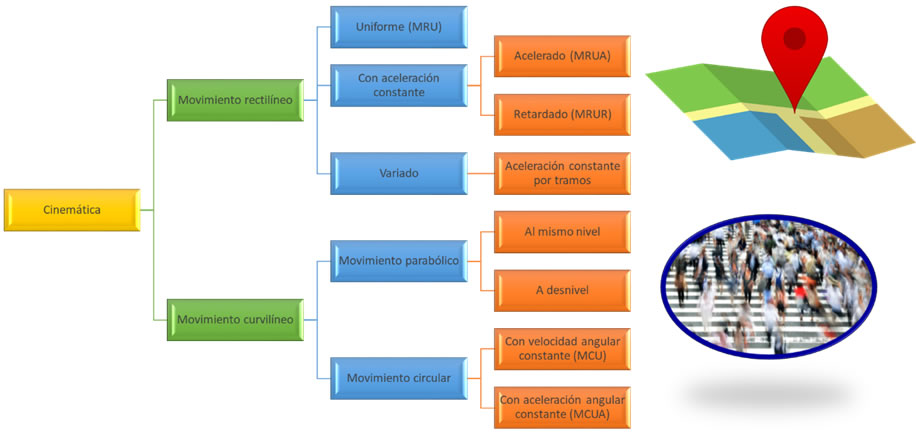
Clasificación de los tipos de movimiento estudiados en cinemática de una partícula, en una y dos dimensiones.

El movimiento de las partículas se suele describir a partir de ciertos parámetros, tales como:

Tiempo (t): es una cantidad escalar considerada en cinemática como una variable independiente, ya que sobre él no se tiene control.

Posición (\(\vec r\)): es una cantidad vectorial que indica la ubicación de la partícula en un instante de tiempo y la dimensión asociada a esta magnitud es la longitud. Ahora bien, el cambio de posición, se denomina desplazamiento (), y se determina con la diferencia de la posición final menos la inicial. Para trayectorias rectilíneas, el módulo del desplazamiento, coincide con la distancia recorrida.

Velocidad (\(\vec v\)): es una cantidad vectorial que expresa el cambio de posición de la partícula respecto al tiempo cuyas dimensiones expresan en longitud dividida entre el tiempo. A la magnitud de la velocidad instantánea se le conoce como rapidez. Matemáticamente, la velocidad instantánea se define como:

\(\vec v = \frac{{d\vec r}}{{dt}}\)

Aceleración (\(\vec a\)): es un vector que representa la variación de la velocidad de una partícula con respecto al tiempo. En el sistema internacional de unidades, la aceleración es una cantidad derivada y sus dimensiones se expresan en longitud sobre el tiempo al cuadrado. La aceleración instantánea se define como:

\(\vec a = \frac{{d\vec v}}{{dt}}\)

Movimiento en una dimensión

Movimiento rectilíneo uniforme (MRU)

Como su nombre lo indica, se trata de un movimiento en el cual la partícula describe una trayectoria rectilínea a velocidad constante, lo que implica que no hay aceleración; en otras palabras, la partícula recorre distancias iguales en intervalos de tiempos iguales. La ecuación general que caracteriza a este tipo de movimiento es:

Ecuación de posición – tiempo: \(\vec r = \pm {\vec r_o} \pm \vec v \cdot t\)

En la imagen se muestra una pelota que se desliza por una superficie horizontal, y en intervalo de tiempo estudiado se observa que el vector velocidad permanece constante en magnitud, dirección y sentido.

Movimiento rectilíneo uniformemente acelerado/retardado (MRUA/MRUR)

Se trata de un movimiento en línea recta en el cual la velocidad de la partícula cambia a lo largo del tiempo por lo que aparece el vector aceleración, el cual se supone constante en magnitud, dirección y sentido. Las principales ecuaciones para este tipo de movimiento son:

Ecuación de posición – tiempo: \(\vec r = \pm {\vec r_o} \pm {\vec v_0} \cdot t \pm \frac{1}{2} \cdot \vec a{t^2}\)

Ecuación de velocidad – tiempo: \(\vec v = \pm {\vec v_o} \pm \vec \cdot t\)

Ecuación de velocidad – posición: \({v^2} = {v_0}^2 \pm 2 \cdot r\)

En las ecuaciones, \({r_0},{v_0}\) representan la posición inicial y la velocidad inicial respectivamente.

Un caso particular del MRUA es el de caída libre, es decir, un movimiento vertical en el cual la única fuerza que actúa sobre la partícula es la gravitatoria (se desprecia la resistencia del aire) y la aceleración que interviene es la de la gravedad (\(\vec a = – \vec g\) ya que es vertical hacia abajo).

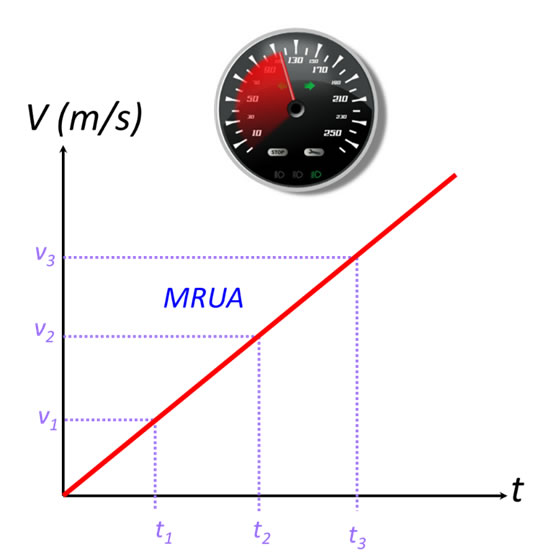
En el MRUA, la gráfica de velocidad contra tiempo se caracteriza por ser una recta inclinada. Si la pendiente es positiva, la aceleración también lo es; y si la pendiente es negativa, la aceleración igualmente lo será, puesto que la aceleración instantánea representa la pendiente de la recta tangente a una curva en un diagrama de velocidad versus tiempo.

Nota: cuando en un estudio la aceración es constante (o nula) en determinados tramos, el análisis se realiza por cada tramo, y la condición inicial de un tramo es la final del tramo precedente.

Movimiento en dos dimensiones

Movimiento parabólico

Es un movimiento curvilíneo que se origina cuando una partícula es lanzada en un campo gravitatorio con un ángulo de inclinación diferente de 90º respecto al eje horizontal. Debido a la atracción de la gravedad, la partícula no describe una trayectoria rectilínea sino una curvilínea en forma de parábola equilátera. Las ecuaciones generales que describen este movimiento son:

Ecuación de posición – tiempo: \(\vec r = \pm {\vec r_o} \pm {\vec v_0} \cdot t \pm \frac{1}{2} \cdot \vec a{t^2}\)

Sus componentes escalares serían:

\(x = {x_0} + {v_0} \cdot cos\alpha \cdot t\)

\(y = {y_0} + {v_0} \cdot sen\alpha \cdot t – \frac{1}{2} \cdot g \cdot {t^2}\)

Ecuación de velocidad – tiempo: \(\vec v = \pm {\vec v_o} \pm \vec \cdot at\)

Sus componentes escalares serían:

\({v_x} = {v_0} \cdot cos\alpha = constante\)

\({v_y} = {v_0} \cdot sen – g \cdot t\)

Ecuación de trayectoria: \(y = {y_0} + tan\alpha \left( {x – {x_0}} \right) – \frac{{g{{\left( {x – {x_0}} \right)}^2}}}{{2 \cdot {v_0}^2 \cdot co{s^2}\alpha }}\)

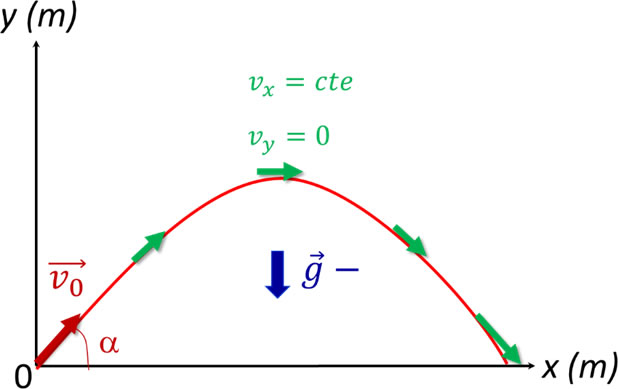
La gráfica muestra la trayectoria parabólica de una partícula lanzada con una inclinación respecto a la horizontal. En color verde se destacan los vectores de velocidad tangencial y en color azul, la aceleración de la gravedad.

Movimiento circular

En un caso específico del movimiento curvilíneo donde la partícula describe una trayectoria circular de radio constante. Las principales ecuaciones en función del tiempo que describen este movimiento son:

Ecuación de posición – tiempo: \(\vec \theta = \pm {\vec \theta _o} \pm {\vec \omega _0} \cdot t \pm \frac{1}{2} \cdot \vec \alpha {t^2}\)

Ecuación de velocidad – tiempo: \(\vec \omega = \pm {\vec \omega _o} \pm \vec \alpha \cdot t\)

Donde θ, ω y α son la posición, velocidad y aceleración angular respectivamente.

Un ejemplo de trayectoria circular es el descrito por la partícula “P” ubicado en el borde del rodillo de la aplanadora en movimiento que se muestra en la imagen.

Nota: los movimientos parabólicos y circulares son casos particulares del movimiento curvilíneo.

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

Art. actualizado: Octubre 2022; sobre el original de julio, 2009.

Datos para citar en modelo APA: Marín, E. M. (Octubre 2022). Definición de Cinemática. Significado.com. Desde https://significado.com/cinematica/