Significado de cuartiles Definición, ejemplos, y de distribución

Doctor en Ingeniería
Definición formal
En estadística, existen varias medidas que nos ayudan a caracterizar la distribución de los datos. En particular, un cuartil es cada uno de los tres puntos de corte que dividen las observaciones de cierto valor de los datos en cuatro intervalos de igual probabilidad.
Explicado en la práctica, supongamos que tenemos un curso con 11 alumnos, y que (como es tradición) la maestra los hace ordenarse de más bajo a más alto. Si el alumno que quedó en el medio mide 1.30m, Q2 = 1.3 es entonces la mediana de la distribución de las alturas, también llamada segundo cuartil. Así mismo, la altura del alumno que quedó en la tercera posición determina el valor del primer cuartil, Q1, y la altura del alumno en la posición nueve corresponde al tercer cuartil, Q3.

En términos generales, los cuartiles pueden definirse como:
Q1: El valor de la observación que está en el medio entre el mínimo y la mediana.
Q2: La mediana o valor intermedio de la distribución.
Q3: El valor de la observación que está en el medio entre la mediana y el máximo.
A partir de estas definiciones, los cuatro intervalos determinados por los tres puntos de corte tienen la misma probabilidad, ya que en cada uno hay igual cantidad de alumnos.
Ejemplos: ¿Cómo se calculan los cuartiles?
Comencemos por la mediana Q2, que es el cuartil más sencillo de calcular. Supongamos que tenemos N muestras ordenadas, donde \(x_n
– Si N es par, en cambio, no hay un elemento que esté exactamente en el medio. Es decir, habría que elegir entre \(x_{N/2}\) y \(x_{N/2+1}\). La solución más común es tomar el promedio entre estos dos valores \(Q_2 = \frac{1}{2}(x_{N/2}+x_{N/2+1})\).
La solución de tomar el valor medio tiene sentido para el ejemplo de las alturas, ya que el promedio entre dos alturas siempre será una altura válida. No obstante, si nuestras observaciones son valores discretos, este podría no ser el caso. Si en lugar de comparar las alturas de los alumnos comparásemos el talle de remera, y \(x_{N/2} =3\) y \(x_{N/2+1} =4\), la mediana ajustada con promedio nos daría un talle 3.5, que no existe y según el contexto puede representar un problema. Por eso a veces, simplemente, se elije.
Para calcular Q1 y Q3 podemos encontrar problemas similares. Después de «cortar la distribución por la mediana» y quedarnos con la primera mitad, podemos optar por incluir o no esa mediana para asegurarnos de que el número de elementos sea impar, y así tomar el elemento del medio. Si volvemos a ver el ejemplo de los 11 alumnos, allí excluimos la mediana para poder calcular Q1 con los 5 primeros elementos, ya que incluirla habría significado tener que elegir Q1 entre 6 elementos. Lo análogo ocurre para calcular Q3.
Hay algunas variantes para hacer estos cálculos, pero no existe un método que sea mejor que los otros. Lo importante es elegir un método que tenga sentido en el contexto del problema que estemos trabajando.
Cuartiles de distribución
Cuando calculamos cuartiles en una distribución de probabilidad, lo que buscamos es que los intervalos que quedan definidos entre ellas tengan igual probabilidad. En distribuciones continuas, como la Normal o la Exponencial, esto es:
\(P(X\leq Q_1) = 0.25\) .
\(P(Q_1 Si conocemos la función de distribución \(\pi(x)\), esto equivale a cortar el área bajo la curva en cuatro partes iguales, es así que \(\int_{-\infty}^{Q_1}\pi(x) dx = \int_{Q_1}^{Q_2}\pi(x) dx = \int_{Q_2}^{Q_3}\pi(x) dx = \int_{Q_3}^{\infty}\pi(x) dx = 0.25\) , suponiendo que la distribución esté definida en \(\mathbb{R}\). Este cálculo resulta muy sencillo si conocemos la Función de Distribución Acumulativa de la distribución. Finalmente, si la distribución de probabilidad es discreta, tenemos un problema similar al que encontramos para el cálculo sobre las observaciones. De nuevo, no hay una regla estricta ni método que sea mejor para todo, y el cálculo debe ajustarse a las características del problema.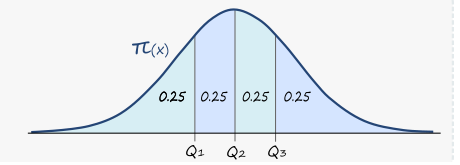

Trabajo publicado en: Ene., 2021.