Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

Se lo describe como un tipo de energía vinculante al movimiento de un cuerpo. Se trata de una cantidad escalar que, conjuntamente con la energía potencial, conforma una componente de la energía mecánica.

Este concepto se relaciona con el hecho de que el trabajo de una fuerza es el producto escalar de la fuerza por el desplazamiento, y todo desplazamiento no nulo implica un cambio de posición, es decir, movimiento; por esta razón, todo cuerpo que se mueva con cierta rapidez posee un tipo de energía de tipo cinética denotada como E_c.

Las turbinas eólicas funcionan a partir de la energía cinética del viento para convertirla en energía mecánica y luego en electricidad.

Con el fin de obtener una expresión para determinar la energía cinética, se supondrá un objeto de masa “m” que se desplaza sobre una superficie horizontal como consecuencia de una \(\sum \vec F\), que de acuerdo con la segunda ley de Newton, produce una aceleración en la misma dirección.

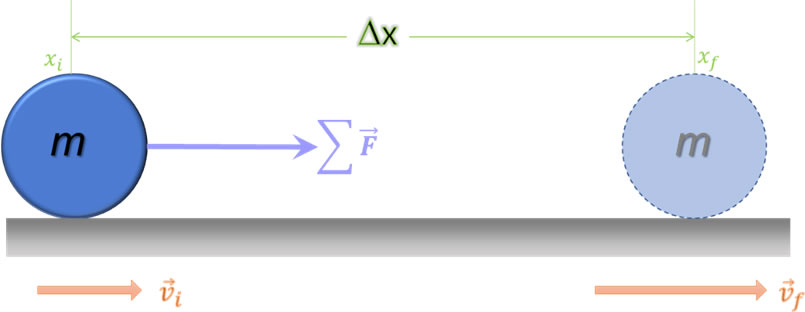
De acuerdo con la segunda ley de Newton, cuando sobre un cuerpo actúa una fuerza neta desequilibrada, el cuerpo presentará una aceleración directamente proporcional a la fuerza aplicada e inversamente proporcional a su masa.

Aplicando la definición del trabajo realizado por una fuerza variable (Text), se tiene:

\({T_{ext}} = \mathop \smallint \nolimits_{{x_i}}^{{x_f}} \sum Fdx\)

Siendo:

xi, xf, las coordenadas de posición inicial y final del desplazamiento

Sustituyendo la fuerza por el producto de la masa por la aceleración \(\sum F = m \cdot a\), se obtiene:

\({T_{ext}} = \mathop \smallint \nolimits_{{x_i}}^{{x_f}} \left( {m \cdot a} \right)dx\)

Puesto que la aceleración se define como el cambio de velocidad respecto al tiempo, la expresión queda:

\({T_{ext}} = \mathop \smallint \nolimits_{{x_i}}^{{x_f}} \left( {m \cdot \frac{{dv}}{{dt}}} \right)dx\)

Utilizando la regla de la cadena, se tiene:

\({T_{ext}} = \mathop \smallint \nolimits_{{x_i}}^{{x_f}} m \cdot \frac{{dv}}{{dx}} \cdot \frac{{dx}}{{dt}}dx = \mathop \smallint \nolimits_{{v_i}}^{{v_f}} m \cdot v.dv\)

El trabajo realizado por la sumatoria de las fuerzas externas sobre el cuerpo de masa constante, resulta:

\({T_{ext}} = \frac{1}{2}m{v_i}^2 – \frac{1}{2}m{v_f}^2\)

El trabajo realizado por una fuerza sobre una partícula en movimiento se obtiene por la diferencia del término \(\frac{1}{2}m{v^2}\) evaluado en los puntos extremos de la trayectoria estudiada. El nombre que recibe cada uno de estos términos es “energía cinética”:

\({E_c} = \frac{1}{2}m{v^2}\)

Como se observa, la energía cinética de un cuerpo varía con la masa y con el cuadrado de la velocidad, y sus unidades en el Sistema Internacional son Joules o Julio (J).

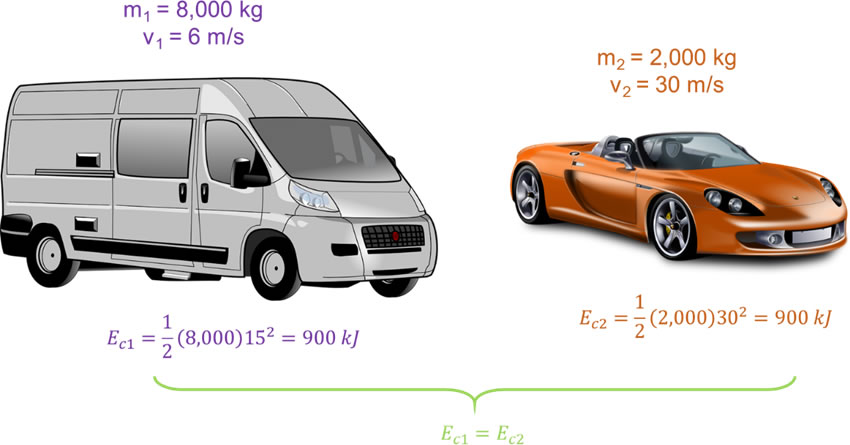
La energía cinética de un camión de 8,000 kg que se desplaza con una rapidez de 15 m/s es igual a la de un auto de 2,000 kg que lleva una rapidez de 30 m/s.

Teorema del trabajo y la energía cinética

En la expresión que determinaba el trabajo realizado sobre un cuerpo (o también aplica para un sistema de partículas) es equivalente al cambio de energía cinética en dicho cuerpo o sistema. De este hecho se concluye que “si el único cambio producido por el trabajo realizado sobre un sistema es la variación de su rapidez, entonces el trabajo neto aplicado sobre dicho sistema es equivalente al cambio de energía cinética”.

\({T_{ext}} = \frac{1}{2}m{v_i}^2 – \frac{1}{2}m{v_f}^2 = {E_{ci}} – {E_{cf}} = Δ{E_c}\)

Este teorema es aplicable para movimientos tanto de traslación como de rotación, y evidencia que si la rapidez del cuerpo disminuye, el trabajo es negativo y si la rapidez se incrementa, el trabajo resultará positivo.

Ejemplo aplicando el concepto de energía cinética

Determine la velocidad final de un cuerpo de 6 kg que inicialmente se encuentra en reposo y sobre el cual actúa una fuerza neta externa constante de magnitud 100 N para desplazarlo a una distancia de 15 m en la misma dirección de la fuerza.

Solución: Aunque este problema se puede abordar a partir de un análisis dinámico para obtener la aceleración, y luego aplicando las ecuaciones de cinemática se puede calcular la velocidad final solicitada, en este caso, se resolverá mediante los conceptos de trabajo y energía.

Partiendo del hecho de que el trabajo efectuado por una fuerza constante se obtiene de la expresión:

\(T = F \cdot Δr \cdot cos\theta \)

Donde:

T: trabajo efectuado por la fuerza constante
Δr: desplazamiento del cuerpo
θ: ángulo formado entre la fuerza y el desplazamiento

Como en el caso analizado la fuerza y el desplazamiento se encuentran en la misma dirección, θ = 0° y cosθ = 1.

El trabajo realizado sobre el cuerpo es:

\(T = 100\;N \cdot 15\;m = 1,500\;J\)

Por otra parte, se conoce que el único efecto sobre el cuerpo producido por la fuerza neta resultó en un cambio de rapidez, lo que significa que es aplicable el teorema del trabajo y la energía cinética; por lo tanto:

\(T = \frac{1}{2}m{v_f}^2 – \frac{1}{2}m{v_i}^2\)

Conociendo que el cuerpo parte del reposo (vi = 0) y despejando la velocidad final, se obtiene:

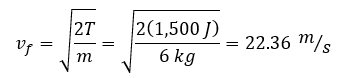
Esto indica que la rapidez final del cuerpo fue de 22.36 m/s.

Nota: es importante acotar que el teorema del trabajo y la energía cinética solo se puede aplicar cuando el único efecto producido por la fuerza sobre el cuerpo o sistema es el de un cambio de rapidez.

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

Art. actualizado: Nov. 2022; sobre el original de noviembre, 2009.

Datos para citar en modelo APA: Marín, E. M. (Nov. 2022). Definición de Energía Cinética. Significado.com. Desde https://significado.com/energia-cinetica/