Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

Estática es el área de la Física mecánica que estudia los cuerpos rígidos en reposo sometidos a la acción de fuerzas (en ocasiones también llamadas cargas estructurales). Específicamente, la estática, forma parte de la mecánica racional, pero se enfoca en el análisis de los cuerpos que se encuentran en equilibrio estático.

La estática, como área del conocimiento, es fundamental para el análisis de estructuras, tanto mecánicas (como las máquinas y bastidores), como las estructuras civiles (vigas, entramados, armaduras o cerchas); y esto se debe a que gran parte de los problemas que se abordan en resistencia de materiales o estructuras, parten de un análisis estático en el cual se determinan las reacciones que producen las cargas, ya sea en los apoyos, en las uniones o a lo largo de todo el elemento estructural.

Desde hace cientos de años, el hombre ha utilizado la estática para el diseño y construcción de estructuras, y aún en la actualidad, se continúan aplicando los mismos principios.

Una de las premisas en las que se basa la estática, es que los cuerpos que se estudian son rígidos, es decir, cuerpos sólidos indeformables constituidos por sistemas de partículas. Esto es una idealización, puesto que en la práctica, todos los cuerpos se deforman (al menos a nivel microscópico) cuando se le aplican fuerzas, sin embargo, esta suposición, permite la determinación de reacciones, y posteriormente, aplicando la mecánica de materiales, se analizan los esfuerzos y deformaciones.

Bajo la premisa de los cuerpos rígidos, se pueden analizar innumerables sistemas que al menos a nivel macroscópico no se observa deformación significativa, tales como, los puentes, edificios, andamios, etc.

Condiciones de equilibrio estático

Como mencionado, la estática se centra en el análisis de los cuerpos en reposo en condiciones de equilibrio estático, es decir, para cuerpos que no se mueven ni en traslación, ni en rotación.

El equilibrio estático implica que el cuerpo no se mueve, lo que a su vez quiere decir, que todas las fuerzas y momentos que actúan sobre él se contrarrestan o anulan para equilibrarlo. La mujer de la imagen realiza una postura de yoga logrando que su centro de gravedad quede alineado con los puntos de apoyo (palmas de la mano)

En el caso de las partículas, por ser representadas mediante un punto geométrico (sin dimensiones), basta con aplicar la primera ley de Newton (\(\sum \vec F = \vec 0\)) para garantizar el equilibrio estático de la misma, ya que al no tener dimensiones, no posee radio para girar y la única posibilidad de movimiento sería la de translación, la cual se imposibilita al igualar la fuerza resultante a cero.

Sin embargo, en el caso de los cuerpos rígidos, por tratarse de un sistema de partículas con dimensiones, el punto de aplicación de la(s) fuerza(s), puede, además de traslación, causar rotación. Por esta razón, en estática, se debe anular la posibilidad de rotación de los cuerpos indicando que el par resultante (sumatoria de momentos) es nulo. Es decir, que las ecuaciones principales a aplicar para el análisis estático de los cuerpos se desprenden de la ley de inercia y expresan que el objeto estudiado no se mueve:

\(\sum \vec F = \vec 0\) ⟶ significa que la sumatoria de fuerzas (fuerza resultante) es nula.

\(\sum \vec M = \vec 0\) ⟶ implica que la sumatoria de pares (momento resultante) es cero.

Estas dos ecuaciones vectoriales, pueden también aplicarse de forma escalar, dependiendo si el análisis se realiza en dos o tres dimensiones. Para el caso del equilibrio estático en el plano (supongamos plano xy), el sistema de ecuaciones escalares puede ser de tres tipos:

Dos sumatorias de fuerzas en el plano y una sumatoria de momento en el eje perpendicular a dicho plano:

\(\sum {F_x} = 0\)

\(\sum {F_y} = 0\)

\(\sum {M_{pz}} = 0\)

Donde “p” es un punto arbitrario sobre el plano que contiene a las sumatorias de fuerzas.

Una sumatoria de fuerzas y dos sumatorias de momentos:

\(\sum {F_{eje}} = 0\)

\(\sum {M_{pz}} = 0\)

\(\sum {M_{qz}} = 0\)

Donde “p” y “q” son puntos arbitrarios sobre el plano perpendicular a z. El “eje” donde se aplica la sumatoria de fuerzas, debe estar contenido en el plano.

Tres sumatorias de momentos:

\(\sum {M_{pz}} = 0\)

\(\sum {M_{qz}} = 0\)

\(\sum {M_{rz}} = 0\)

Nota: para que los sistemas de ecuaciones escalares generen solución única, se debe garantizar que sean linealmente independientes, lo que significa que “p”, “q” y “r”, no deben ser puntos colineales.

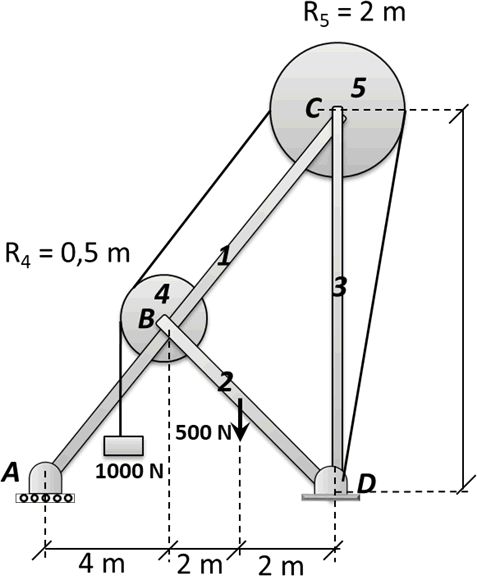
Ejemplo de una suposición bidimensional para un entramado, ya que en la realidad, todos los cuerpos son tridimensionales.

El análisis estático es de gran utilidad para calcular reacciones (fuerzas o momentos) en las uniones de los elementos estructurales, o en los apoyos.

Cuando el análisis estático se aplica a un cuerpo tridimensional, el sistema de ecuaciones escalares en general, debe contener seis ecuaciones, por ejemplo:

\(\sum {F_x} = 0\)

\(\sum {F_y} = 0\)

\(\sum {F_z} = 0\)

\(\sum {M_{px}} = 0\)

\(\sum {M_{py}} = 0\)

\(\sum {M_{pz}} = 0\)

En la práctica, las estructuras y objetos son tridimensionales, aunque bajo ciertas suposiciones, algunos análisis se pueden realizar en dos dimensiones.

Electricidad estática

La estática, como área de la Física, suele referirse al campo de la mecánica (mecánica estática o mecánica racional), sin embargo, la palabra estática significa reposo (sin movimiento), lo que quiere decir que también es aplicable a fenómenos relacionados a la electricidad y también al magnetismo.

Específicamente, la electrostática es una rama de la Física eléctrica que estudia las fuerzas y campos eléctricos generados por cargas eléctricas en reposo, abarcando también el estudio de la electricidad estática. Las ecuaciones que se suelen aplicar en este tipo de análisis, son distintas a las empleadas en la mecánica estática.

Lo más habitual, es abordar los problemas de cálculo de fuerzas electrostáticas (de atracción o repulsión), a partir de la ley de Coulomb:

\(F = k\frac{{{q_1} \cdot {q_2}}}{{{r^2}}}\)

Donde:

F: fuerza electrostática (N)
k = constante de Coulomb (9×10⁹ N.m²/C²)
q₁ y q₂ son las magnitudes de las cargas eléctricas (C)
r: distancia de separación de las cargas (m)

En la imagen se observa el efecto de la estática en una lámpara o bola de plasma.

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

Art. actualizado: Nov. 2022; sobre el original de diciembre, 2008.

Datos para citar en modelo APA: Marín, E. M. (Nov. 2022). Definición de Estática. Significado.com. Desde https://significado.com/estatica/