Definición de Figuras Geométricas

Ingeniera Industrial, MSc en Física, y EdD
1. Conjunto de formas dadas a partir de la manipulación del punto y la línea recta-curva, donde se configuran cuerpos cerrados-sólidos cuyas propiedades lineales de altura y ancho están estandarizados universalmente para reconocerse por el nombre que define cada uno, tal es el caso del cuadrado (cuatro lados iguales), el triángulo (tres lados iguales), o el círculo (una línea curva en función de su circunferencia).
Etimología: Figura, por el latín figūra. + Geométrica, por el latín geometrĭca, femenino de geometrĭcus, sobre el griego, γεωμετρική (geōmetrikḗ), femenino de γεωμετρικός (geōmetrikós), formado por el prefijo griego γεω- (geō-), de γῆ (gê), por ‘tierra’, y metrikḗ, por ‘métrica’ en cuanto a la medición..
Cat. gramatical: Sustantivo fem.
En sílabas: fi-gu-ra + ge-o-mé-tri-ca.
Figuras Geométricas
 La figura geométrica es un conjunto cuyos componentes resultan ser puntos (uno de los entes fundamentales de la geometría), en tanto, es la Geometría la disciplina que se ocupará de su estudio detallado, de sus principales características: su forma, su extensión, sus propiedades y su posición relativa.
La figura geométrica es un conjunto cuyos componentes resultan ser puntos (uno de los entes fundamentales de la geometría), en tanto, es la Geometría la disciplina que se ocupará de su estudio detallado, de sus principales características: su forma, su extensión, sus propiedades y su posición relativa.
La figura geométrica se define como un conjunto no vacío que está compuesto por puntos y comprendidas como un lugar geométrico, configurando un área cerrada por líneas o superficies, ya sea en un plano o en el espacio.
Con el solo hecho de ponernos a observar la naturaleza, el mundo que nos rodea, podemos confirmar la existencia y presencia de las más variadas formas en los cuerpos materiales que conviven en la mencionada naturaleza y entonces, es de estos que nos vamos formando la idea de volumen, superficie, línea y de punto. Los diferentes tipos de necesidades a las cuales se ha ido enfrentando el hombre a través de los años han generado que este se ponga a pensar y a estudiar diferentes técnicas que le permitan, por ejemplo, construir, desplazarse o medir y en este camino devino el hombre en el uso de las diversas figuras geométricas.
Figuras geométricas elementales
Las figuras geométricas más elementales resultan ser las siguientes: el plano, el punto, la recta, en tanto, las mismas como consecuencia de transformaciones y desplazamientos de sus componentes producen diferentes volúmenes, superficies y líneas que son en definitivas el objeto de estudio de la Geometría, la topología y las matemáticas, entre otras. Las mencionadas figuras de acuerdo a la función que presentan se clasifican en cinco tipos: Adimensional, el punto; Unidimensional, la recta (semirrecta y segmento) y la curva; Bidimensional, el plano, delimitando superficies (el polígono, el triángulo y el cuadrilátero), la sección cónica incluye a elipses, circunferencias, parábola e hipérbola, describiendo superficies (superficie reglada y superficie de revolución; Tridimensional, nos encontramos con aquellas que delimitan volúmenes, el poliedro y aquellas que en cambio describen volúmenes, sólido de revolución, cilindro, esfera y cono; y las N-Dimensional, como el politopo. Por ejemplo, el cuadrilátero y el triángulo resultan ser figuras geométricas sólidas que delimitan volúmenes.
El triángulo es una de las figuras geométricas más reconocidas y populares. Básicamente, se trata de un polígono compuesto por tres lados. A mencionada figura del triángulo es lograda a partir de la unión de tres rectas que se interceptarán en tres puntos no alineados, mientras tanto, cada uno de estos puntos en donde es posible que las rectas se unan se denominan como vértices y los segmentos que se conforman se llamarán lados. Existen diversas maneras a la hora de clasificar a esta figura geométrica, por la amplitud de sus ángulos (rectángulo, acutángulo y obtusángulo), por la longitud de sus lados (equilátero, isósceles, escaleno). Por su parte, el cuadrado es otra de las figuras geométricas por excelencia. Se trata de un polígono compuesto por cuatro lados iguales y paralelos y sus ángulos miden todos 90°, siendo estas sus características salientes y definitorias.
Figuras geométricas planas
Las figuras geométricas pueden representarse dos dimensiones, en cuyo caso forman figuras planas, y reciben el nombre de polígono cuando sus lados son todos rectos. Son configuraciones de líneas curvas o rectas que se unen para generar un contorno cerrado con dimensiones asociadas a un plano. Estas figuras pueden tener formas regulares o irregulares, por ejemplo, las regulares se asocian con formas definidas como los círculos o los polígonos regulares, mientras que las irregulares no poseen una forma definida, sino abstracta.

Las figuras geométricas constituyen todas las formas que conocemos. Algunas figuras planas poseen forma irregular y no están asociadas a algún polígono o figura con nombre conocido, por ejemplo, la corteza de un árbol tiene escamas de formas irregulares.
Los polígonos
Son figuras geométricas planas y cerradas que tienen todos sus lados rectos. Su clasificación puede hacerse considerando diversos criterios, como sus ángulos internos, la cantidad de lados o sus dimensiones. Los elementos principales que conforman a un polígono son:
Lados: representan los bordes o segmentos que definen y limitan el contorno de la figura.
Ángulos internos: son los ángulos formados dentro del polígono por dos lados consecutivos.
Vértice: es el punto donde se unen dos lados consecutivos, es decir, las esquinas del polígono.
Diagonales: son segmentos que conectan dos vértices opuestos y no consecutivos del polígono. Existe una relación entre el número de diagonales (ND) de un polígono y la cantidad de lados (n) del mismo, y se calcula con la siguiente ecuación:
\({N_D} = \frac{{n\left( {n – 3} \right)}}{2}\)
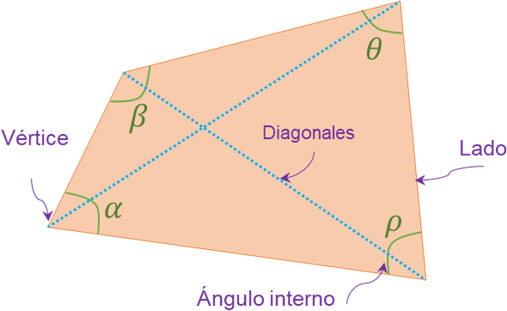
Los elementos principales de un polígono son sus lados, ángulos internos, vértices y diagonales.
¿Sabías que? Las figuras planas compuestas por lados rectos se llaman polígonos y las formas tridimensionales compuestas por planos se denominan poliedros.

Una tendencia artística conocida como arte prismático, consiste en formar imágenes a partir de polígonos.
Clasificación de los polígonos
Los polígonos pueden ser clasificados considerando diversos aspectos de sus elementos. A continuación se describen algunos tipos de polígonos:
Según sus ángulos internos:
Polígonos cóncavos: son aquellos polígonos que poseen al menos un ángulo interno mayor de 180°.

La estrella de seis puntas es un polígono cóncavo que posee doce vértices y en seis de ellos tiene ángulos mayores de 180°.
Polígonos convexos: son los polígonos que tiene todos sus ángulos internos menores a 180°.

Los panales de abejas están formados por hexágonos, que son polígonos convexos, ya que todos sus ángulos internos son menores a 180°.
Según el número de lados:
No hay un límite en cuanto al número de lados en un polígono, pero al menos debe tener tres lados. A continuación se nombran algunos de estos:
Triángulos: son polígonos compuestos por tres lados, tres vértices y tres ángulos internos.
Cuadriláteros: son polígonos compuestos por cuatro lados, cuatro ángulos internos, cuatro vértices y dos diagonales.
Pentágono: son los polígonos regulares formados por cinco lados iguales y cinco ángulos internos iguales.

El Pentágono es el edificio donde se encuentra el Departamento de Defensa de Estados Unidos, y debe su nombre a la forma de su estructura.
Hexágonos: son polígonos regulares de seis lados iguales y seis ángulos internos iguales.
La siguiente tabla muestra otros tipos de polígonos regulares y sus nombres considerando la cantidad de lados:
| Polígono | Cant. lados | Cant. diagonales | Medida de cada ángulo interno |
|---|---|---|---|
| Heptágono | 7 | 14 | 128.57° |
| Octágono | 8 | 20 | 135° |
| Eneágono | 9 | 27 | 140° |
| Decágono | 10 | 35 | 144° |
| Endecágono | 11 | 44 | 147.27° |
| Dodecágono | 12 | 54 | 150° |

La imagen muestra algunos polígonos regulares como el hexágono, heptágono, octágono y el decágono.
Áreas y perímetros
El área de una figura plana representa el espacio bidimensional ocupado por la superficie delimitada por el contorno de la figura y se expresa en dimensiones de longitud al cuadrado. Por otra parte, el perímetro constituye la medida o longitud del contorno de la figura y para los polígonos, se determina mediante la suma de las medidas de sus lados, por lo tanto, sus dimensiones son de longitud. Las fórmulas de áreas (A) y perímetros (P) de algunas figuras planas comunes se muestran en la siguiente tabla:
| Figura | Parámetros | Área | Perímetro |
|---|---|---|---|
Triángulo
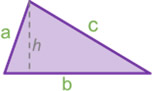 |
b: base h: altura a,b,c: lados |
\(A = \frac{{b \times h}}{2}\) | \(P = a + b + c\) |
Cuadrado
 |
l: lados | \(A = {l^2}\) | \(P = 4l\) |
Rectángulo
 |
b: base h: altura |
\(A = b \times h\) | \(P = 2b + 2h\) |
Rombo
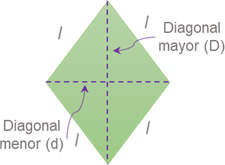 |
b: base h: altura |
\(A = \frac{{d \times D}}{2}\) | \(P = 4l\) |
Romboide
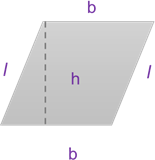 |
b: base h: altura l: lado |
\(A = b \times h\) | \(P = 2\left( {l + b} \right)\) |
Trapecio
 |
b: base menor B: base mayor h: altura l: lado a:lado |
\(A = \left( {\frac{{b + B}}{2}} \right) \times h\) | \(P = b + B + l + a\) |
Círculo
 |
r: radio | \(A = \pi \times {r^2}\) | \(P = 2\pi r\) |
Siga en Figuras Geométricas (parte 2)

Art. actualizado: Dic. 2022; sobre el original de diciembre, 2009.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.