Significado de función exponencial Definición, ejemplos, gráfica creciente y decreciente

Doctora en Matemática
Definición formal
Las funciones exponenciales son funciones de una variable real (dominio en los números reales) que se caracterizan por poseer una tasa de crecimiento directamente proporcional al valor de la función. Esta particularidad permite que modelen eficazmente muchas situaciones de la naturaleza, la informática e incluso de la economía.
Se identifica generalmente con una expresión de la forma
\(f(x)=a^x, \quad a>0 \quad \text{y}\quad a\neq 1.\qquad (1)\)
La variable x se encuentra en el exponente y la base de dicha potencia es una constante positiva, distinta de 1. Sin embargo, en algunos casos también se identifican con este concepto otras funciones de la forma
\(f(x)=a^{g(x)}\)
para ciertas funciones \(g(x)\), como por ejemplo \(f(x)=3^{2x-1}\). El hecho de excluir como base al número 1 se reduce a que, en este caso, \(f(x)=1^x=1\) y por lo tanto la función es equivalente a una función constante.
Representación gráfica: función exponencial creciente y decreciente
Las funciones definidas como en (1) poseen una representación gráfica característica. En primer lugar, las curvas que representan estas funciones pasan siempre por el punto (1, 0) para cualquier valor de a, puesto que \(f(0)=a^0=1\).
Por otro lado, poseen una asíntota horizontal en el eje x (y = 0) y a la vez son funciones que tienden a infinito. Esta ultima característica se debe a que este tipo de funciones son estrictamente crecientes o estrictamente decrecientes dependiendo del valor de a.
Analicemos esto a partir de algunos ejemplos:
\(f(x)=2^x,\qquad h(x)=e^x \qquad \text{y}\qquad g(x)=\left(\frac12 \right)^x.\)
La función h tiene como base al número irracional e = 2, 71828…. Dicho número es muy utilizado en aplicaciones matemáticas y, por ello, la función exponencial con base e suele llamarse “la” función exponencial. A partir de la figura que se encuentra a continuación, que representa las gráficas de las funciones anteriores, podemos observar que todas se intersecan en el punto mencionado (0, 1).
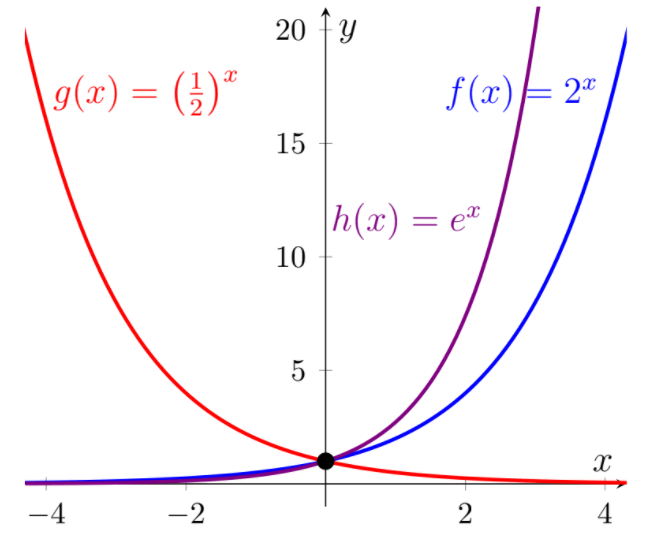
Además, las funciones f y h tienen como asíntota al eje x, para valores muy chicos de x (es decir, cuando x tiende a −∞) y ambas funciones tienden a infinito cuando x toma valores muy grandes (es decir, cuando x tiende a ∞). En particular, se puede probar que esto sucede siempre que la contante a en (1) satisfaga a > 1 y la función será creciente.
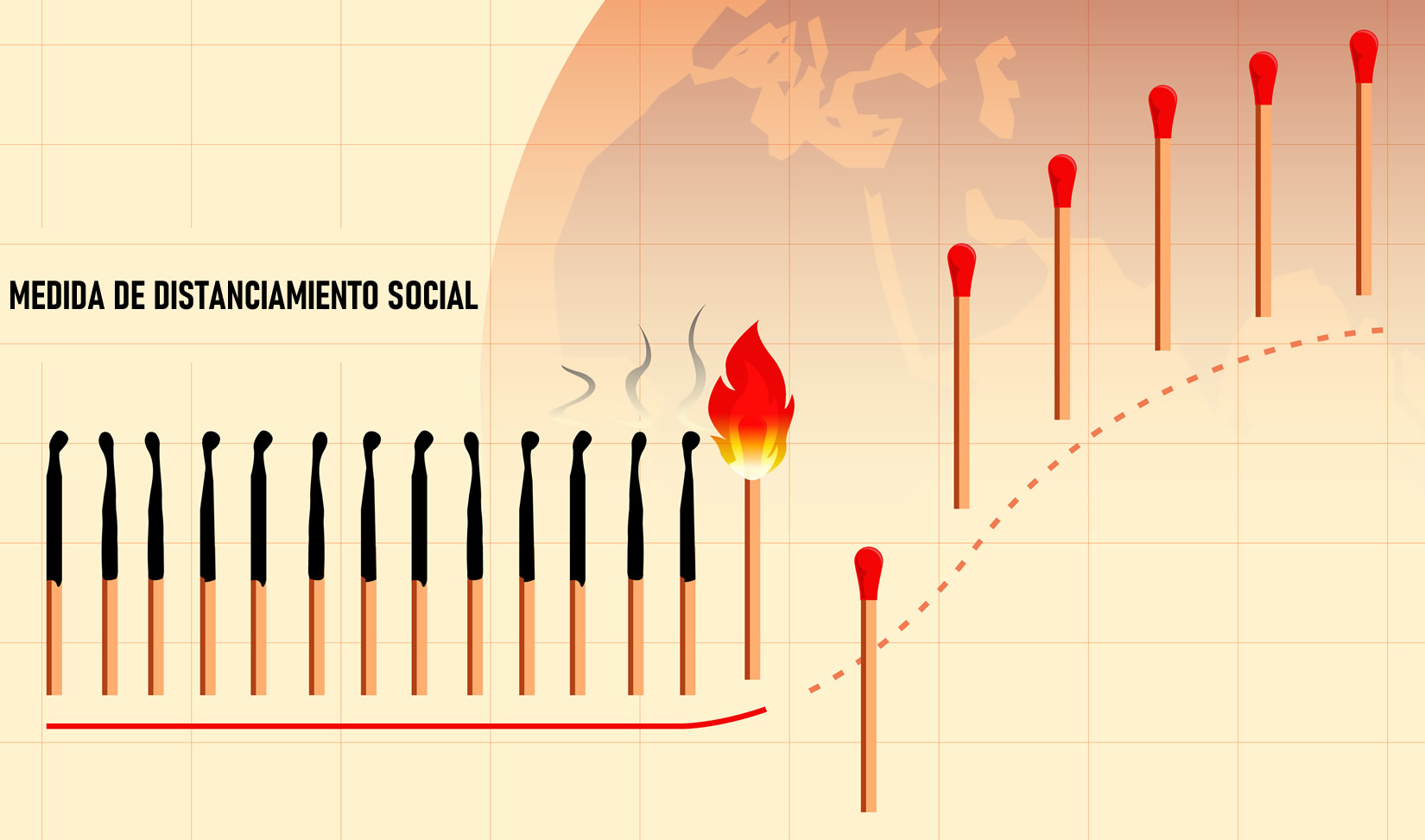
En el caso de la función g, esto se invierte; posee una asíntota en el eje x cuando x tiende a ∞ y la función toma valores muy grandes cuando x tiende a −∞. De manera similar al caso anterior, se puede probar que esto se satisface siempre que \(0 Las funciones exponenciales son una herramienta muy utilizada en el modelado de distintas situaciones de la vida cotidiana, desde fenómenos de la naturaleza hasta problemas de las ciencias económicas. La siguiente tabla presenta algunas de las aplicaciones más populares. En el 2020, en los inicios de la pandemia de coronavirus 19 (COVID-19), el modelo matemático que utiliza crecimiento exponencial para el número de infectados en cada país o región fue muy popular. Este modelo no contempla los casos de personas recuperadas, ni los fallecidos, por lo que solo se puede utilizar para modelar el crecimiento inicial de la pandemia en una zona. Si consideramos la cantidad de infectados por coronavirus diarios en un área específica, podría modelarse la cantidad de infectados a futuro (manteniendo las mismas condiciones de circulación de la población del lugar). En particular, sin ningún tipo de restricción sobre la población ni cuidados adicionales, se estima que un infectado por COVID-19 puede infectar entre 1,5 y 2,5 personas en promedio. Afortunadamente, esta no es la base de la función exponencial, puesto que intervienen otros factores tales como el número de personas que superaron la enfermedad, las medidas higiénicas, el confinamiento, etc. En términos generales, el modelo para la etapa inicial de la pandemia puede formalizarse como: \(I(t)=(E\cdot P+1)^t\) donde I(t) es el número de infectados en tiempo t, E es una constante que depende del nivel de exposición de los infectados, y P es una contante que depende de la probabilidad de contagio (puede ser menor a la antes mencionada en función de la higiene y los cuidados implementados). La función crecerá con menor velocidad si el producto de E · P tiende a cero y eso, en estas condiciones, sucederá si algunas de las constantes (o ambas) tienden a cero. En particular, la constante E tiende a cero si se puede disminuir la exposición de los infectados, ya sea detectándolos con rapidez para aislarlos o disminuyendo la exposición de toda la población. A su vez, P tiende a cero al disminuir la probabilidad de contagio, lo que se puede realizar aumentando los cuidados, maximizando la higiene e instalando el uso de barbijos o cubrebocas.
Aplicación
Fórmula
Referencias
Crecimiento poblacional exponencial
\(P(t)=P_o e^{rt}\)
P: población;
P0: población inicial;
r: constante de crecimiento;
t: tiempo.
Desintegración radiactiva
\(N(t)=N_o e^{-\lambda t}\)
N0: cantidad inicial de núcleos radioactivos;
λ : (λ > 0) constante de desintegración;
t: tiempo.
Interés compuesto
\(C(p)=C_o (1+e)^{p}\)
C: capital;
C0: capital inicial;
p: período de tiempo.Función exponencial aplicado al COVID-19
Siga en Función Exponencial (parte 2)

Trabajo publicado en: Ene., 2021.