Significado de inecuaciones Definición, ejemplos, intervalo, conjunto y gráfica

Licenciada en Física
Definición formal
Una inecuación consiste en la comparación de dos cantidades no equivalentes, las cuales contienen una o más incógnitas, por lo que la expresión se cumple únicamente para un determinado conjunto de valores.
Simplificando, una inecuación es una desigualdad que contiene una o más cantidades desconocidas. A su vez, una desigualdad consiste en establecer que una determinada cantidad es diferente de otra. Algunas desigualdades pueden ser verdaderas y otras falsas, por ejemplo:
• 2 es estrictamente menor que 5 (Verdadera)
• −3 es mayor o igual que 10 (Verdadera)
• 4 es mayor o igual que 6 (Falsa)
Desde luego, hay símbolos matemáticos para expresar las desigualdades en forma compacta:
• Mayor que: >
• Menor que: <
• Mayor o igual que: ≥
• Menor o igual que: ≤
Con esta notación, las desigualdades anteriores se escriben así:
• 2 < 5
• −3 ≥ 10
• 4 ≥ 6
Como se puede ver, estas expresiones no contienen alguna cantidad desconocida, sino que se limitan a establecer una relación de orden entre dos números. En cambio, una inecuación contiene al menos una cantidad desconocida, como las que siguen:
• x > 3
• 5 − 2x ≤ 8
• x + y > −3
Hay diversos tipos de inecuaciones, pero en líneas generales se clasifican en:
• Polinómicas (lineales, de segundo grado, con valor absoluto…)
• Racionales
Resolver una inecuación significa encontrar el conjunto de valores que la cumplen. Por ejemplo la inecuación x > 3 se satisface con el conjunto de números reales estrictamente mayores que 3 y este hecho se puede expresar de tres formas.
Notación de intervalo
Un intervalo se indica usando paréntesis o corchetes, según si los valores extremos pertenecen o no al conjunto numérico que se quiere expresar.
Por ejemplo, todos los números mayores que 3 se escribirían en notación de intervalo así:
(3, ∞+)
Donde se usó un paréntesis para indicar que el 3 no pertenece a la solución, y otro paréntesis para indicar que el valor de ∞+ no se conoce con exactitud. Si el 3 perteneciera a la solución, entonces el intervalo se escribiría con un corchete encerrando el 3, así: [3, ∞+).
En general, los intervalos cuyos extremos son dos números reales a y b pueden ser:
• Abiertos por ambos lados, por lo que a y b no se incluyen en el conjunto: (a,b)
• Cerrados por ambos lados para incluir ambos, a y b: [a,b]
• Abiertos por la izquierda y cerrados por la derecha, a no está incluido pero b sí: (a,b]
• Abiertos por la derecha y cerrados por la izquierda, a se incluye pero b no: [a,b)
Y siempre que el intervalo contenga al infinito, siempre se coloca abierto por ese lado.
Notación de conjunto
Continuando con el ejemplo anterior, todos los números reales mayores o iguales a 3 también se puede escribir de esta forma:
S = {x є R / 3 < x < ∞+} Los símbolos son los siguientes: • Pertenece a: є • Conjunto de los números reales: R • Tales que: / Y la expresión entre las llaves se lee así: “Todos los valores de x pertenecientes al conjunto de los números reales, tales que x está comprendido entre 3 e infinito positivo”.
Notación gráfica
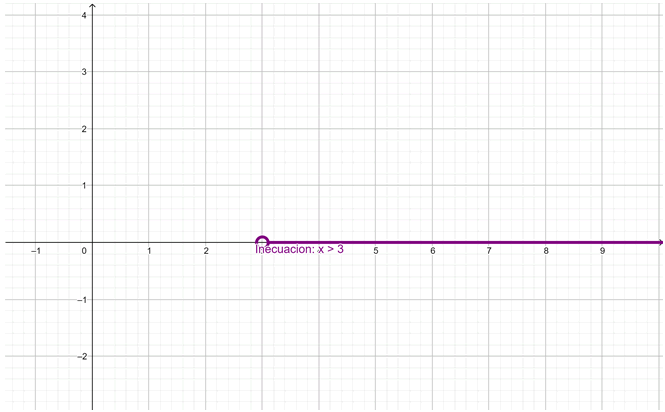
La solución también se puede dibujar sobre un gráfico hecho o mano o con una calculadora en línea. El círculo abierto en x = 3 significa que este valor no está incluido en la solución.
Propiedades de las desigualdades
Las propiedades de las desigualdades se aplican en la resolución de las inecuaciones:
1.- Sumar o restar una misma cantidad a los dos miembros de una desigualdad no la altera en absoluto, por ejemplo:
\(a
3.- Si se multiplican ambos miembros de una desigualdad por una cantidad positiva, la desigualdad no se altera, pero si la cantidad es negativa, el sentido de la desigualdad se invierte:
\( a>b,\text{ }c<0\Rightarrow a\cdot c
Pero si la cantidad “c” es negativa, entonces el sentido de la desigualdad se invierte:
\(a>b\text{, y c}<\text{0}\Rightarrow \frac{\text{a}}{\text{c}}<\frac{b}{c}\)
Ejemplos resueltos
Ejemplo 1: Resolver 5 − 2x ≤ 8
Respuesta: Para encontrar la solución es necesario despejar la incógnita, al igual que se hace con una ecuación, por lo tanto, lo primero es aislar el término que contiene la “x” y dejarlo solo a la izquierda de la desigualdad. Se puede aplicar la propiedad 2 para transponer el “5”:
5 − 2x ≤ 8
5 − 2x −5 ≤ 8 − 5
− 2x ≤ 3
Ahora se divide cada miembro entre −2, y como es un valor negativo, el sentido de la desigualdad se invierte:
\(\frac{-2x}{-2}\le \frac{3}{-2}\Rightarrow x\ge -\frac{3}{2}\)
El conjunto solución es el intervalo cerrado por la izquierda, ya que −3/2 pertenece a la solución y abierto por la derecha:
[−3/2, ∞+)
Gráficamente:
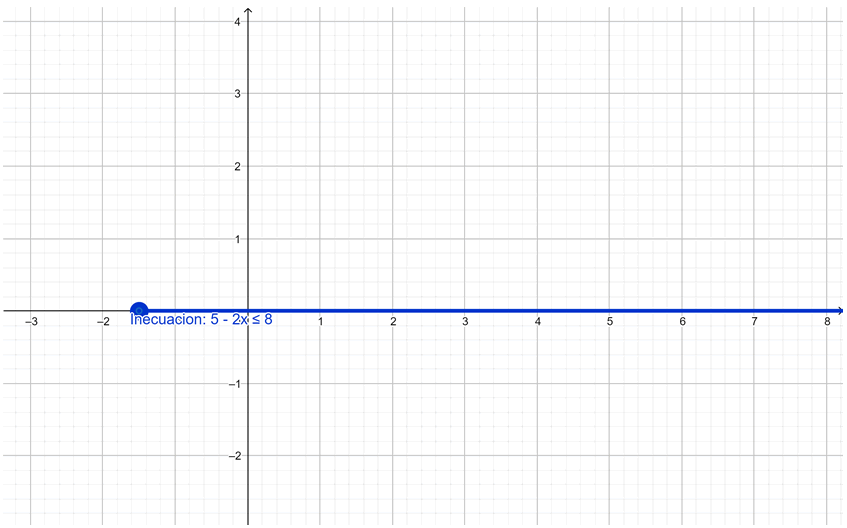
El lector puede comprobar por sustitución directa que cualquier valor que pertenezca al intervalo solución satisface la desigualdad. Por ejemplo, eligiendo arbitrariamente x = 10:
5 − 2∙10 ≤ 8
5−20 ≤ 8
−15 ≤ 8
En cambio, si escoge un valor fuera del intervalo solución, como x = −2, se tiene:
5 − 2∙(−2) ≤ 8
Pero 5+4 = 9, y 9 no es menor o igual a 8
Ejemplo 2: Resolver
\(\frac{x-2}{x-1}\ge 0\)
Respuesta: Esta es una inecuación de tipo racional, y se requiere que el cociente sea positivo (mayor que 0). La única forma de obtener esto es que el numerador y el denominador tengan el mismo signo.
Caso 1
El numerador y el denominador son ambos positivos, entonces:
• x−2 ≥ 0 → x ≥ 2
• x−1 > 0 → x > 1
Importante: la división por 0 no está definida, por lo tanto x tiene que ser diferente a 1, de lo contrario el denominador se anula. Es la razón de que x > 1 en vez de x ≥1. El numerador puede anularse sin problema en este caso.
La solución es la intersección de ambos conjuntos:
x ≥ 2 o [2, ∞+)
Caso 2
El numerador y el denominador son ambos negativos, por lo que:
• x−2 ≤ 0 → x ≤ 2
• x−1 < 0 → x < 1
La solución es la intersección de ambos conjuntos:
x < 1 o bien (−∞, 1)
Una vez analizados los casos posibles, la solución definitiva de la inecuación planteada es la unión de ambos conjuntos:
(−∞, 1) U [2, ∞+)
Lo anterior se puede resumir en esta tabla, que se construye colocando en la primera columna los factores que intervienen en la desigualdad. En este caso son x−2 y x−1, de los que se hallan los respectivos ceros: x = 2 y x =1.
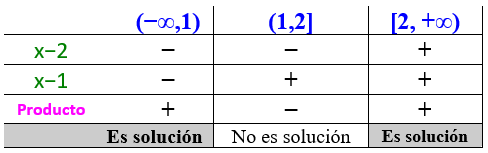
Con los ceros de cada factor se construyen los intervalos mostrados en la primera fila (azul) y en cada casilla va el signo del factor a la izquierda, cuando se sustituye en él un valor arbitrario de x que pertenezca a dicho intervalo.
Por ejemplo, x−2 es negativo si se elige un valor que pertenezca al intervalo (−∞,1), entonces ese signo se coloca en la fila de x−2 y debajo de dicho intervalo. Se procede del mismo modo para el resto de los intervalos y para el siguiente factor.
Luego se multiplican los signos debajo de cada intervalo, como la inecuación es mayor o igual que 0, solo los productos con signo + son solución de la ecuación, es decir, los intervalos (−∞,1) y [2, +∞).
En forma gráfica, la solución queda:
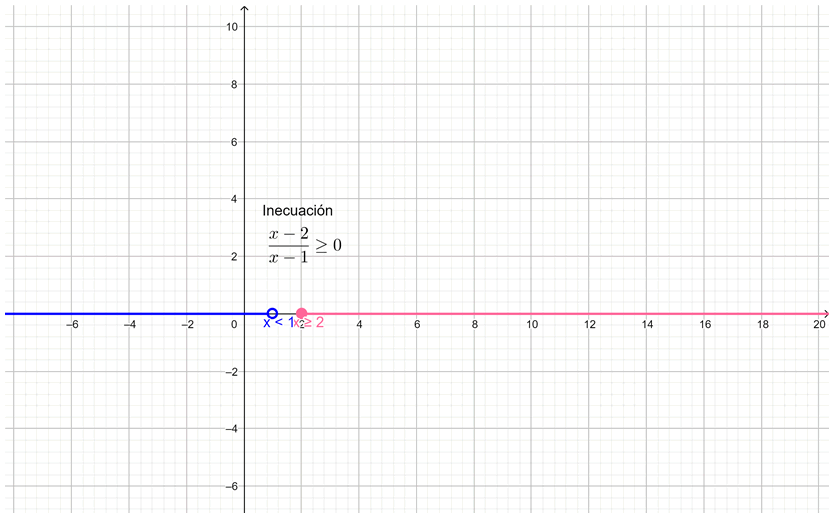

Trabajo publicado en: Ene., 2021.