Definición de Interferencia (ondas)

Ángel Zamora Ramírez
Licenciado en Física

La interferencia es un fenómeno que ocurre cuando dos o más ondas se encuentran en el mismo espacio y se superponen entre sí. Esta interferencia puede causar que las ondas se complementen y resulte una onda con igual o mayor amplitud, o que las ondas se cancelen y no exista una onda resultante.

Si alguna vez le ponemos atención a un cuerpo de agua, podemos observar cómo en su superficie se forman ondas como consecuencia de la interacción con el aire, de algunos objetos que caen e incluso por los organismos que ahí viven. Si observamos con más detenimiento nos percataremos que algunas de estas ondas en su propagación terminan encontrándose, formando nuevas ondas o aniquilándose mutuamente. Este es un ejemplo del fenómeno de interferencia en acción.

Función de onda, amplitud y fase

Consideremos una onda que se propaga en una dimensión. La posición de esta onda y su evolución temporal puede ser descrita por medio de una función \(u(x,t)\), la cual puede ser escrita de la siguiente manera:

\(u\left(x,t\right)=A\sin{(kx-\omega t)}\)

Donde A es la amplitud de la onda, k es conocido como el “número de onda” y \(\omega\) es la frecuencia angular. El número de onda \(k\) está relacionado con la longitud de onda \(\lambda\), de tal manera que:

\(k=\frac{2\pi}{\lambda}\)

Por otro lado, la frecuencia angular \(\omega\) está relacionada con la frecuencia \(f\) de la onda, esta relación establece que:

\(\omega=2\pi\ f\)

La amplitud A de la onda es la distancia que existe entre el punto máximo o mínimo que alcanza la onda (cresta o valle, respectivamente) y su posición de equilibrio. En otras palabras, la amplitud es una medida de lo amplia o estrecha que es una oscilación y está directamente relacionada con la energía que transporta una onda.

Podemos darnos cuenta entonces que en la función de onda \(u(x,t)\) están incluidas todas las propiedades importantes de la onda, como su frecuencia, su longitud de onda y su amplitud. Además, de que describe como esta onda se propaga por el espacio y como evoluciona en el tiempo.

Otra cosa que podemos agregar a nuestra función de onda es una “fase”. La fase es una especie de condición inicial que nos establece el estado angular de la onda en el tiempo \(t=0\) y cuando se encuentra en su posición inicial \(x=0\). Sea \(\phi\) la fase de la onda \(u(x,y)\), esta la podemos incorporar como:

\(u\left(x,t\right)=A\sin{(kx-\omega t+\phi)}\)

De tal manera que:

\(u\left(x=0,t=0\right)=A\sin{(\phi)}\)

Con esto ya estamos listos para explorar el fenómeno de interferencia.

Ecuaciones y elementos en las Interferencias

Consideremos dos ondas que se propagan simultáneamente en una dimensión. Por simplicidad vamos a suponer que ambas ondas poseen la misma amplitud A, el mismo número de onda k y la misma frecuencia angular \(\omega\). Lo único que las diferencia es que se encuentran en fases diferentes, es decir, se encuentran desfasadas por un cierto ángulo \(\phi\). Sea y_\(1(x,t)\) la función de la primera onda y \(y_2(x,t)\) la función de la segunda onda, estas funciones las escribiremos como:

\(y_1\left(x,t\right)=A\sin{(kx-\omega t)}\)

\(y_2\left(x,t\right)=A\sin{(kx-\omega t+\phi)}\)

Nótese que hemos introducido la fase \(\phi\) en la función \(y_2(x,t)\) para representar el desfase que existe entre ambas ondas. Como ambas ondas se propagan en la misma dimensión y se encuentran en el mismo espacio, se obtendrá una nueva onda \(Y(x,t)\) producto de la interferencia entre ambas y que será simplemente la suma de las dos funciones. Es decir que:

\(Y\left(x,t\right)=y_1\left(x,t\right)+y_2(x,t)\)

Sustituyendo las dos funciones de onda obtenemos:

\(Y\left(x,t\right)=A\sin{(kx-\omega t+\phi)}+A\sin{(kx-\omega t)}\)

Podemos factorizar el término A, de tal manera que:

\(Y\left(x,t\right)=A[\sin{\left(kx-\omega t+\phi\right)}+\sin{\left(kx-\omega t\right)}]\)

Recordemos que si tenemos dos ángulos cualesquiera \(\alpha\) y \(\beta\), entonces se cumple que:

\(\sin{\alpha}+\sin{\beta}=2\sin{\left(\frac{\alpha+\beta}{2}\right)}\cos{\left(\frac{\alpha-\beta}{2}\right)}\)

Podemos utilizar esta identidad en la suma de las funciones de onda. Tomando en cuenta esto se obtiene:

\(Y\left(x,t\right)=A\left[2\sin{\left(\frac{\left(kx-\omega t+\phi\right)+(kx-\omega t)}{2}\right)}\cos{\left(\frac{\left(kx-\omega t+\phi\right)-(kx-\omega t)}{2}\right)}\right]\)

Desarrollando la suma y la esta en la ecuación anterior nos lleva a:

\(Y\left(x,t\right)=2A\cos{\left(\frac{\phi}{2}\right)}\sin{\left(kx-\omega t+\frac{\phi}{2}\right)}\)

Esta es la función de la onda resultando de la interferencia. Nótese que la amplitud de la nueva onda es:

\(A^\prime=2A\cos{\left(\frac{\phi}{2}\right)}\)

Donde A\prime es la amplitud resultante. También nos damos cuenta de que la amplitud de la nueva onda depende de la diferencia de fase \(\phi\) que existe entre las dos ondas iniciales. Con esto en nuestras manos podemos explorar dos escenarios.

Notemos que el valor máximo que puede alcanzar la amplitud A\prime ocurre cuando \(\cos{\left(\phi/2\right)}=1\), y esto a su vez ocurre cuando \(\phi=\pm\ 4n\pi\), donde \(n=0,1,2,\ldots,\infty\). En estos casos \(A^\prime=2A\). Además, esto coincide con el periodo de las funciones seno y coseno. Por lo tanto, la función de la onda resultante en este caso estará dada por:

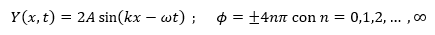
Este es el caso en el que se tiene una interferencia constructiva y podemos darnos cuenta de que la onda resultante posee una amplitud igual al doble de la amplitud original.

Por otro lado, tenemos la situación en donde \(A^\prime=0\). Esto puede ocurrir si \(\cos{\left(\phi/2\right)}=0\). Esto es válido para \(\phi=\pm\ n\pi\) con \(n\) siendo cualquier número natural impar. En este caso la amplitud es nula y, por lo tanto, no existe función de onda. Podemos decir entonces que:

\(Y\left(x,t\right)=0\ para\ \phi=\pm\ n\pi\ con\ n\ impar\)

Esta es la situación en la que la interferencia de ambas ondas es destructiva, y conlleva a que las dos ondas se cancelen y no existe una onda resultante de la interferencia. Con estos dos pequeños ejercicios nos percatamos que la diferencia de fase entre ambas ondas tiene un impacto en el tipo de interferencia que tendrán entre sí.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Abr., 2024.

Datos para citar en modelo APA: Zamora Ramírez, A. (abril, 2024). Definición de Interferencia (ondas). Significado.com. Desde https://significado.com/interferencia/