Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

Un paralelogramo es una configuración geométrica plana basada en cuatro lados y vértices caracterizada por dos elementos clave: 1) la longitud de sus lados, definidos en dos pares de líneas, donde cada una está en oposición y dispuesta de forma paralela a su respectivo par, constituyendo de este modo sus cuatro lados, y 2) la clase de ángulos, vista en pares, que pueden ser rectos (como en el cuadrado y el rectángulo), o congruentes (como en el rombo y el caso particular del romboide, como un hijo del rombo y el rectángulo). Permite calcular áreas y perímetros de diferentes figuras.

Etimológicamente, paralelogramo procede de la influencia del francés parallélogramme, sobre el latín tardío parallelogrammum, respecto del griego παραλληλόγραμμον (parallēlógrammon), formado por parallēlus, de paralelo, determinado por el prefijo παρα- (para-), en cuanto ‘al lado’, y ἀλλήλων (allḗlōn), de ‘otro’; y el sufijo -γράμμα (-grámma), que remite en este contexto a cada línea, en referencia a la ‘forma escrita’ (del mismo que aplica para ‘letra’ en anagrama).

Las tres figuras mostradas en la imagen representan paralelogramos, ya que están conformadas por cuatro lados, paralelos dos a dos.

Clasificación de los paralelogramos

Hay tres tipos principales de paralelogramos: el cuadrado, el rombo y el rectángulo.

• El cuadrado posee cuatro lados y cuatro ángulos rectos (90 grados).

Una de las formas más básicas en geometría es el cuadrado, el cual se trata de un paralelogramo que posee todos sus lados con la misma medida y sus cuatro ángulos internos de 90°. Los marcos de cada ventana del edificio son cuadrados

• El rombo posee cuatro lados iguales y solo dos pares de ángulos congruentes.

El borde de la placa que contiene la cerradura tiene forma de rombo, el cual constituye uno de los tipos de paralelogramo.

• El rectángulo tiene solo los lados opuestos iguales y los cuatro ángulos rectos.

Las tarjetas de créditos tienen forma rectangular (despreciando la curvatura de las esquinas), por lo tanto, su contorno representa un ejemplo de paralelogramo.

Para determinar el área y el perímetro de un paralelogramo, se deben conocer las longitudes de sus lados y su altura.

Calcular el perímetro de un paralelogramo

– El perímetro (P) es la suma de las longitudes de los cuatro lados, es decir:

P = 2a + 2b

Donde a y b son los lados opuestos del paralelogramo.

Ejemplo: Determina el perímetro de un rombo cuyos lados tienen la misma longitud, y cuyas diagonales miden 5 m y 8 m.

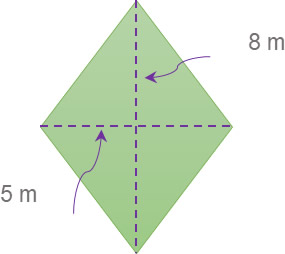
Solución: Cuando se conocen las medidas de las diagonales del rombo, se puede aplicar el teorema de Pitágoras para hallar la longitud de un lado. La longitud de los lados (s) sería:

\(s = \sqrt {{{\left( {\frac{{{d_1}}}{2}} \right)}^2} + {{\left( {\frac{{{d_2}}}{2}} \right)}^2}} = \sqrt {\frac{{{d_1}^2}}{4} + \frac{{{d_2}^2}}{4}} = \frac{{\sqrt {{d_1}^2 + {d_2}^2} }}{2}\)

donde d1 y d2 son las diagonales del rombo.

Es importante destacar que las diagonales de un rombo se intersectan en el punto medio de ambas.

Si las diagonales miden 5 m y 8 m, entonces el lado es s = \(\frac{{\sqrt {{d_1}^2 + {d_2}^2} }}{2}\) ≈ 4.72 m y el perímetro es P = 4 x 4.72 ≈ 18.88 m.

Nota: En el caso particular del cuadrado, sus lados son todos iguales (a), por lo tanto, su perímetro se puede expresar como:

P_cuadrado = 4a

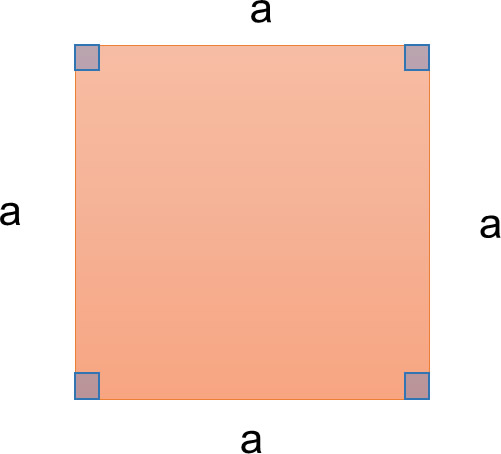
El perímetro se expresa en unidades de longitud, por ejemplo, centímetros.

Calcular el área de un paralelogramo

El área es el producto de la longitud de la base por la altura, es decir:

A = b x h

donde b es la base y h es la altura perpendicular a la base.

• En el caso de los rombos, si se conocen sus diagonales, el área se determina como el producto de sus diagonales dividido a la mitad:

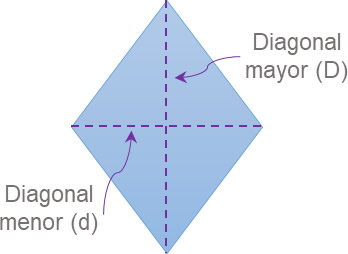
\({A_{rombo}} = \frac{{D \times d}}{d}\)

Donde D y d son las diagonales mayor y menor respectivamente.

Por otra parte, en el caso del cuadrado, como todos sus lados son iguales, su área equivale al doble de sus lados.

Las unidades de área son unidades de longitud al cuadrado, por ejemplo, metros cuadrados (m²).

Ejemplo: Un padre posee un terreno rectangular de 50 m por 40 m, y desea repartirlo de manera equitativa entre sus 10 nietos:

a) ¿Qué área debe tener la parcela que le corresponde a cada nieto?
b) Proponga una distribución de manera que se obtengan 10 parcelas rectangulares con las mismas dimensiones. ¿Qué dimensiones (base y altura) debe tener cada parcela?

Solución:
a) Para determinar las dimensiones del área que le correspondería a cada nieto, simplemente se determina el área total del terreno completo y el resultado se divide entre 10:

\({A_{total}} = \frac{{base \times altura}}{{10\;\left( {hijos} \right)}} = \frac{{50\;m \times 40\;m}}{{10}} = 200\;{m^2}\)

b) Ahora bien, un posible arreglo o distribución de las parcelas, de manera que todas tengan las mismas dimensiones, puede ser dividiendo la base entre 5, [(50 m ÷ 5) = 10 m] y la altura entre 2, [(40 m ÷ 2) = 20 m], de esta manera, quedarían 10 parcelas rectangulares de 20 m x 10 m cada una:

Propiedades de los ángulos en los paralelogramos

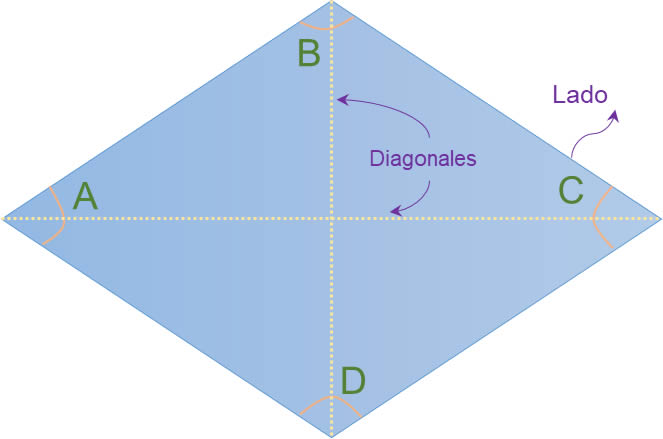
• Los ángulos en oposición expresan la misma medida. Por ejemplo, si el ángulo A mide 60°, entonces el ángulo C también mide 60°.

• Los ángulos adyacentes resultan suplementarios, es decir, suman 180°. Por ejemplo, si el ángulo A mide 60°, entonces el ángulo B mide 120°.

• La suma de los cuatro ángulos interiores es igual a 360°. Por ejemplo, si los ángulos A y C miden 60° cada uno, y los ángulos B y D miden 120° cada uno, entonces la suma es 60° + 120° + 60° + 120° = 360°.

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

Art. actualizado: Marzo 2023; sobre el original de noviembre, 2012.

Datos para citar en modelo APA: Marín, E. M. (Marzo 2023). Definición de Paralelogramo. Significado.com. Desde https://significado.com/paralelogramo/