Definición de Péndulo

Ángel Zamora Ramírez
Licenciado en Física

Un péndulo es un sistema físico cuya configuración consta de una masa suspendida de un punto perteneciente a un eje horizontal. La masa de un péndulo se suspende por medio de un hilo o una cuerda que aporta cierta tensión y evita que caiga. Esta configuración hace que un péndulo presente un movimiento oscilatorio gracias a la fuerza de gravedad cuando la masa es movida de su punto de equilibrio.

Los péndulos son un ejemplo perfecto de un sistema clásico que presenta un movimiento periódico, y también sirven para visualizar la conservación de la energía mecánica. Estos objetos han tenido diversas aplicaciones a lo largo de la historia, aplicaciones que van desde la fabricación de relojes hasta la medición de la gravedad y rotación de la Tierra.

El péndulo simple

El tipo de péndulo más sencillo de estudiar desde la Física, y también el primer paso para estudiar péndulos más complejos, es el “Péndulo Simple”, que consiste en una masa m suspendida por un hilo de longitud \(l\) cuya masa es mucho más pequeña que la masa m, de tal manera que podemos despreciarla. Un esquema de este sistema lo podemos apreciar en la siguiente figura.

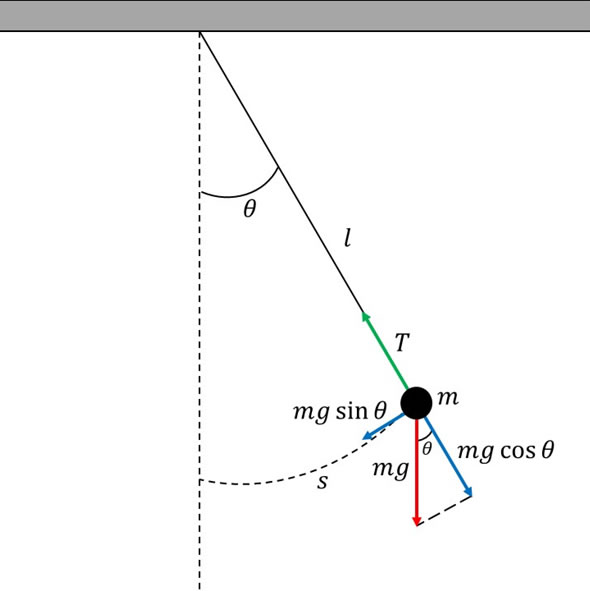
Cuando la masa del péndulo se desplaza de la posición central de equilibrio, comienza a realizar un movimiento oscilatorio debido a la acción de la gravedad. Supongamos que movemos la masa m hasta un ángulo \theta con respecto a la posición de equilibrio y desde esta posición comienza a oscilar, tal como podemos apreciar en la figura anterior.

Existe dos fuerzas que actúan sobre la masa m. La primera es la fuerza de gravedad \(F_g\), la cual es la que genera el movimiento periódico del péndulo. Esta fuerza es:

\(F_g=-mg\)

La otra fuerza presente es la tensión T que ejerce el hilo del cual está suspendida la masa. La tensión evita que la masa se desprenda y caiga por completo. La fuerza de gravedad \(F_g\) se puede separar en dos componentes, una que es opuesta a la tensión T y que denominaremos \(F_{gl}\), y otra que es tangencial a la trayectoria curva descrita por el péndulo en movimiento y que la llamaremos \(F_{gs}\)

Las componentes de la fuerza \(F_g\) son proyecciones que están dadas por el ángulo \(\theta\). Como podemos ver en la figura, estas componentes de la fuerza \(F_g\) están dadas por:

\(F_{gl}=-mg\cos{\theta}\)

\(F_{gs}=-mg\sin{\theta}\)

La componente \(F_{gl}\) se opone a la tensión T, para ser más precisos, estas dos fuerzas están en equilibrio y es esto lo que evita que la masa caiga. Esto implica que:

\(T-mg\cos{\theta}=0\)

Como en esta dirección la suma de las fuerzas es igual a 0, la única fuerza restante es la componente \(F_{gs}\). Podemos decir entonces que la fuerza neta \(F_{net}\) ejercida sobre la masa es simplemente \(F_{net}=F_{gs}. Por lo tanto:

\(F_{net}=-mg\sin{\theta}\)

A su vez, por Segunda Ley de Newton, sabemos que \(F_{net}=ma\). Donde \(a\) es la aceleración. Reemplazando esto en la ecuación anterior se obtiene:

\(ma=-mg\sin{\theta}\)

Eliminando los términos m de ambos lados de la ecuación se obtiene:

\(a=-g\sin{\theta}\)

Si \(r es la posición de una partícula con respecto al tiempo, su aceleración estará dada por:

\(a=\frac{d^2r}{dt^2}\)

En nuestro caso, esta aceleración será la segunda derivada de la longitud de arco s dada por el ángulo \(\theta\) y la longitud l del hilo. Particularmente, podemos decir que \(s=l\theta\). Tomando en cuenta todo esto en la ecuación de movimiento obtenemos:

\(\frac{d^2s}{dt^2}=\frac{d^2}{dt^2}\left(l\theta\right)=-g\sin{\theta}\)

Como \(l es una cantidad constante, la podemos sacar de la derivada y pasarla dividiendo al lado opuesto de la ecuación. Haciendo este obtenemos:

\(\frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin{\theta}\)

De esta manera obtenemos la ecuación de movimiento de un péndulo simple. Esta es una ecuación diferencial ordinaria de segundo orden y resolverla es un tanto complicado, sin embargo, podemos resolverla para un caso particular y es cuando las oscilaciones son pequeñas. Bajo esta condición, el ángulo \(\theta\) desde el que comienzan las oscilaciones es muy pequeño, en este límite específico podemos decir que \(\sin{\theta}\approx\theta\). Para este caso la ecuación anterior se reduce a:

\(\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta\)

El movimiento armónico simple de una partícula cuya posición con respecto al tiempo es x está descrito por la ecuación:

\(\frac{d^2x}{dt^2}=-\omega^2x\)

Donde \omega es la velocidad angular. Esta ecuación es muy similar a la última ecuación que obtuvimos para el péndulo simple, indicando que en este límite describe un movimiento armónico simple. Comparando ambas ecuaciones podemos decir que para el caso del péndulo la velocidad angular está dada por:

\(\omega=\sqrt{\frac{g}{l}}\)

A su vez, la velocidad angular está relacionada con el periodo \(\tau\) de las oscilaciones de la siguiente manera:

\(\omega=\frac{2\pi}{\tau}\)

Sustituyendo esto en la ecuación anterior se tiene:

\(\frac{2\pi}{\tau}=\sqrt{\frac{g}{l}}\)

Resolviendo para \tau obtenemos finalmente que:

\(\tau=2\pi\sqrt{\frac{l}{g}}\)

Como podemos darnos cuenta, el periodo de un péndulo simple depende únicamente de la longitud del hilo y de la aceleración de gravedad. Es esta particularidad la que ha brindado a los péndulos la gran variedad de aplicaciones que tienen.

Modulando la longitud de un péndulo podemos obtener periodos específicos, esto los hizo una gran herramienta para medir el tiempo y hace relojes. También, como el periodo de un péndulo depende de la aceleración de gravedad, se han utilizado péndulos con una longitud dada para medir la aceleración de la gravedad en distintos puntos de nuestro planeta. Finalmente, el Péndulo de Foucalt sirvió para demostrar la rotación de la Tierra.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Abr., 2024.

Datos para citar en modelo APA: Zamora Ramírez, A. (abril, 2024). Definición de Péndulo. Significado.com. Desde https://significado.com/pendulo/