Ángel Zamora Ramírez
Licenciado en Física

El Principio de Bernoulli, muchas veces también llamado Ecuación de Bernoulli, es uno de los conceptos más importantes de la hidrodinámica y de la mecánica de fluidos. Fue formulado por el físico y matemático suizo Daniel Bernoulli en 1738 como parte de su obra “Hidrodynamica” y parte de la conservación de energía en un fluido ideal en movimiento.

Imaginemos la siguiente situación: Tenemos una manguera a través de la cual está fluyendo agua, la cual sale de la manguera con cierta velocidad y cierta presión. Después procedemos a tapar parcialmente el orificio de salida de la manguera con un dedo; al hacer esto vemos cómo el agua ahora sale con mayor velocidad. Esto es un ejemplo del principio de Bernoulli en acción.

Fluidos ideales en movimiento

El principio de Bernoulli aplica en fluidos ideales en movimiento, así que, antes de pasar a explicar este principio, es importante mencionar a qué nos referimos con fluido ideal. Un fluido ideal es una simplificación de un fluido real, esto se hace debido a que la descripción de un fluido ideal es matemáticamente más simple y nos brinda resultados útiles que después pueden extenderse al caso del fluido real.

Hay cuatro suposiciones que se hacen para considerar que un fluido es ideal y todas de ellas tienen que ver con el flujo:

• Flujo estacionario: Un flujo estacionario es aquel en el que la velocidad a la que se mueve el fluido es la misma en cualquier punto del espacio. Dicho de otra manera, suponemos que el fluido no sufre turbulencias.

• Incomprensibilidad: Se asume también que un fluido ideal es incomprensible, es decir, que tiene una densidad constante en todo momento.

• No viscosidad: La viscosidad es una propiedad de los fluidos que en términos generales representa la resistencia que opone el fluido al movimiento. La viscosidad podemos pensarla como análoga a la fricción mecánica.

• Flujo irrotacional: Con esta suposición nos referimos a que el fluido en movimiento no realiza ningún tipo de movimiento circular en torno a ningún punto de su trayecto.

Al hacer estas suposiciones y tener un fluido ideal simplificamos mucho el tratamiento matemático y también aseguramos la conservación de la energía, lo cual es el punto de partida hacia el principio de Bernoulli.

Explicación de la ecuación de Bernoulli

Consideremos a un fluido ideal moviéndose a través de una tubería como se muestra en la figura siguiente:

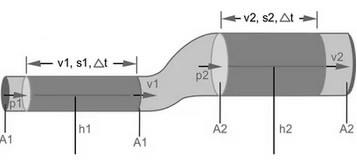
Utilizaremos ahora el Teorema del Trabajo y de la Energía Cinética que es otra forma de expresar la Ley de Conservación de la Energía, esto nos dice que:

\(W = {\rm{\Delta }}K\)

Donde \(W\) es el trabajo mecánico total y \({\rm{\Delta }}K\) es el cambio de energía cinética entre dos puntos. En este sistema tenemos dos tipos de trabajos mecánicos, uno que es hecho por la fuerza de gravedad sobre el fluido y otro que resulta de la presión del fluido. Sea \({W_g}\) el trabajo mecánico hecho por la gravedad y \({W_p}\) el trabajo mecánico hecho por la presión, podemos decir entonces que:

\({W_g} + {W_p} = {\rm{\Delta }}K\)

Como la gravedad es una fuerza conservativa, el trabajo mecánico realizado por esta será igual a la diferencia de energía potencial gravitatoria entre dos puntos. La altura inicial a la que se encuentra el fluido es \({y_1}\) y la altura final es \({y_2}\), por lo tanto, tenemos que:

\({W_g} = – {\rm{\Delta }}mg{\rm{\Delta }}y = – {\rm{\Delta }}mg\left( {{y_2} – {y_1}} \right)\)

Donde \({\rm{\Delta }}m\) es la porción de masa de fluido que pasa por cierto punto y \(g\) es la aceleración de gravedad. Como el fluido ideal es incompresible, entonces \({\rm{\Delta }}m = \rho {\rm{\Delta }}V\). Donde \(\rho \) es la densidad del fluido y \({\rm{\Delta }}V\) es la porción de volumen que fluye por un punto. Sustituyendo esto en la ecuación anterior obtenemos:

\({W_g} = – \rho g{\rm{\Delta }}V\left( {{y_2} – {y_1}} \right)\)

Consideremos ahora el trabajo mecánico realizado por la presión del fluido. La presión es la fuerza ejercida por unidad de área, es decir que \(F = PA\). Por otro lado, el trabajo mecánico está definido como \(W = F{\rm{\Delta }}x\) donde \(F\) es la fuerza aplicada y \({\rm{\Delta }}x\) es el desplazamiento realizado en este caso sobre el eje x. En este contexto podemos pensar en \({\rm{\Delta }}x\) como la longitud de la porción de fluido que fluye por cierto punto. Juntando ambas ecuaciones tenemos que \(W = PA{\rm{\Delta }}x\). Podemos darnos cuenta que \(A{\rm{\Delta }}x = {\rm{\Delta }}V\), es decir, es la porción de volumen que fluye por dicho punto. Por lo tanto, tenemos que \(W = P{\rm{\Delta }}V\).

En el punto inicial se realiza un trabajo mecánico sobre el sistema que es igual a \({P_1}{\rm{\Delta }}V\) y en el punto final el sistema realiza un trabajo mecánico sobre el entorno igual a \({P_2}{\rm{\Delta }}V\). El trabajo mecánico debido a la presión del fluido será entonces el trabajo hecho sobre el sistema menos el trabajo que este realiza sobre su entorno, es decir que:

\({W_p} = {P_1}{\rm{\Delta }}V – {P_2}{\rm{\Delta }}V = \left( {{P_1} – {P_2}} \right){\rm{\Delta }}V\)

Finalmente, la diferencia de energía cinética \({\rm{\Delta }}K\) será igual a la energía cinética en el punto final menos la energía cinética en el punto inicial. Es decir que:

\({\rm{\Delta }}K = \frac{1}{2}{\rm{\Delta }}mv_2^2 – \frac{1}{2}{\rm{\Delta }}mv_1^2 = \frac{1}{2}{\rm{\Delta }}m\left( {v_2^2 – v_1^2} \right)\)

Por lo mencionado anteriormente, sabemos que \({\rm{\Delta }}m = \rho {\rm{\Delta }}V\). La ecuación anterior queda entonces como:

\({\rm{\Delta }}K = \frac{1}{2}\rho {\rm{\Delta }}V\left( {v_2^2 – v_1^2} \right)\)

Sustituyendo todos los resultados obtenidos en la ecuación de conservación de la energía se obtiene que:

\(\left( {{P_1} – {P_2}} \right){\rm{\Delta }}V – \rho {\rm{\Delta }}V\left( {{y_2} – {y_1}} \right) = \frac{1}{2}\rho {\rm{\Delta }}V\left( {v_2^2 – v_1^2} \right)\)

Podemos factorizar el término \({\rm{\Delta }}V\) en ambos lados de la ecuación, esto nos lleva a que:

\({P_1} – {P_2} – \rho g\left( {{y_2} – {y_1}} \right) = \frac{1}{2}\rho \left( {v_2^2 – v_1^2} \right)\)

Desarrollando los productos faltantes tenemos que:

\({P_1} – {P_2} – \rho g{y_2} + \rho g{y_1} = \frac{1}{2}\rho v_2^2 – \frac{1}{2}\rho v_1^2\)

Reacomodando todos los términos en ambos lados de la ecuación obtenemos que:

\({P_1} + \rho g{y_1} + \frac{1}{2}\rho v_1^2 = {P_2} + \rho g{y_2} + \frac{1}{2}\rho v_2^2\)

Esta ecuación es una relación entre el estado inicial y el estado final de nuestro sistema. Podemos decir finalmente que:

\(P + \rho gy + \frac{1}{2}\rho {v^2} = constante\)

Esta última ecuación es la Ecuación de Bernoulli de la cual se deriva su principio. El Principio de Bernoulli es una ley de conservación para un fluido ideal en movimiento.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Ago., 2023.

Datos para citar en modelo APA: Zamora Ramírez, A. (agosto, 2023). Definición de Principio/ecuación de Bernoulli. Significado.com. Desde https://significado.com/principio-bernoulli/