Definición de Probabilidad
Doctor en Psicología
1. La probabilidad son las chances de que algo ocurra o se confirme, con base en la evaluación lógica de un conjunto de informaciones, como situaciones similares positivas y negativas, puntos de interferencia, espacio y tiempo. Ejemplos: A) ‘Mañana hay una alta probabilidad de lluvia’. B) ‘Existe la probabilidad de que esté mintiendo’.
2. Matemáticas. Cálculo sobre cuántas posibilidades existen para un acontecimiento aleatorio ante el total de resultados posibles. El valor obtenido varía linealmente entre 0 (imposible) y 1 (totalmente posible). Ejemplo: ‘La probabilidad de ganar la lotería es de 1 en 50 millones’.
Etimología: Por los modos del latín probabilĭtas, probabilĭtātis, constituido sobre el adjetivo probabĭlis, de ‘probable’, respecto del verbo probāre, de ‘probar’, acompañado del sufijo -ble, con referencia en el latín -bĭlis, de acuerdo a la adjetivación deverbal con propiedad de acción, este último combinado con el sufijo -dad, en latín -tas, -ātis, como -bilidad, conforme agente de cualidad en función de la sustantivación respecto de la forma adjetiva.
Cat. gramatical: Sustantivo fem.
En sílabas: pro-ba-bi-li-dad.
Probabilidad
Básicamente, se define cómo probabilidad el grado de posibilidad de que ocurra o no un evento. Daniel Kahneman, premio nobel en economía, dedica varios pasajes de su obra “Pensar rápido, pensar despacio” a describir cómo los seres humanos necesitamos tener certeza en torno a lo que pasará. Bajo esta premisa, se desarrollan herramientas cognitivas como los heurísticos para tratar de llegar a conclusiones claras sobre los acontecimientos. Sin embargo, el mismo Kahneman declara que muchas de estas conclusiones terminar por ser equivocadas, lo cual resulta ser completamente normal, pues en sus palabras “sería un error culpar a nadie de fracasar en sus predicciones en un mundo improbable” (Kahneman, p.315, 2021).
Debido a esta necesidad intrínseca de certeza sobre los acontecimientos, los seres humanos se han visto en la necesidad de desarrollar heurísticos del pensamiento o ideologías/creencias que proveen de certeza, sin embargo, al ser eximidas a mayor detalle, estas carecen de un sustento sólido. Entonces, ¿cómo podríamos tener mayor certeza sobre los acontecimientos?, la respuesta a esta pregunta puede ser encontrada en la probabilidad, la cual es una disciplina que típicamente se encuentra íntimamente relacionada con la estadística.
Si bien la forma más sencilla de definir a la probabilidad es describiéndola cómo el grado en que es posible que un acontecimiento determinado se produzca, esto puede ser considerado un tanto reduccionista, por lo que es necesario recurrir a otras definiciones que permitan comprender con mayor detalle esta disciplina.
Definición clásica de la probabilidad
La definición clásica indica que en un espacio muestral que contiene una cantidad N de eventos simples, un evento A puede producirse de una cantidad de n maneras distintas; dicho de otra forma, al realizar una simulación/experimento hay N resultados posibles de los cuales n son favorables al evento A. Esta definición es acompañada por la siguiente fórmula.
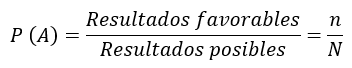
Una de las principales críticas a esta teoría es la siguiente. Cuando se produce un evento A, este puede ser simple o compuesto, si el caso que se nos presenta corresponde al segundo, entonces el determinar todas las formas en que puede producirse un evento se vuelve demasiado complejo. Aunado a lo anterior, la cantidad de elementos que componen el espacio muestral también puede influir en los elementos previamente establecidos.
Definición frecuentista de la probabilidad
Con anterioridad se mencionó el trabajo de Kahneman y se hizo referencia a una frase que permite abordar la teoría frecuentista (“Sería un error culpar a nadie de fracasar en sus predicciones en un mundo improbable”). La definición frecuentista de la probabilidad surge en consecuencia de la presencia de factores y elementos aleatorios que imposibilitan el determinar de manera precisa la probabilidad de un evento. Es decir, cuando es complejo determinar cuántos resultados favorables de un evento existen y, por consiguiente, cuantos resultados posibles pueden presentarse.
La probabilidad desde la perspectiva frecuentista se obtiene mediante la frecuencia relativa, la cual se obtiene la siguiente manera.
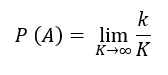
Donde K es el número de ocasiones en que se observa un fenómeno determinado, y k es el número de veces en que un se produce un resultado favorable al evento A. De este modo la probabilidad de que ocurra el evento A es el resultado de la frecuencia relativa observada cuando las observaciones crece de manera indefinida.
Axiomas de la probabilidad
Un axioma es definido cómo un enunciado que no requiere de ser demostrado, así, cada disciplina puede poseer diferentes axiomas asociados a sus campos de estudio. En el caso particular de la probabilidad, el matemático ruso Andréi Kolmogórov (también famoso por la prueba de normalidad univariada) estableció una serie de axiomas matemáticas referentes a este campo.
Axioma 1 (ausencia de negatividad): La probabilidad que se produzca un suceso siempre será positiva o cero; en caso de que se produzca este último fenómeno se le nombrará suceso imposible.
Axioma 2 (certidumbre): Cuando un evento pertenece a E su probabilidad de ocurrencia es 1, es decir, P(E) = 1. También se le llama suceso seguro.
Axioma 3 (edición): Cuando se presentan dos o más eventos incompatibles (A1, A2, A3) la probabilidad de que ocurra cada uno de estos sucesos es la suma de la probabilidad de que suceda cada uno por separado.
Estadística bayesiana
Propuesta por Thomas Bayes, la estadística bayesiana se fundamenta en el teorema de Bayes, que de forma muy resumida nos indica que un evento A puede producirse en función de un evento B. Por lo tanto, en este paradigma se realizan inferencias estadísticas a partir de la interpretación subjetiva de la probabilidad; es decir, con base en la evidencia ¿qué tan probable es que se cumpla una hipótesis? O bien, agregando nueva evidencia ¿qué tan probable es que una hipótesis se mantenga o sea necesario la formulación de una nueva?
Siga en Probabilidad (parte 2)
Art. actualizado: Feb. 2023; sobre el original de diciembre, 2008.
Referencias
Bacchini, R. D., Vázquez, L. V., Bianco, M. J. & García Fronti, J. I (2018). Introducción a la probabilidad y a la estadística (1era. Ed.). Facultad de ciencias Económicas.Cáceres Guido, P., Pavan, C. H., Otamendi, E. & Bramuglia, G. F. (2020). Principios de estadística Bayesiana y su relación con la farmacocinética aplicada. Revista Chilena de Pediatría, 91 (5), 828-837.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.