Definición de Progresión Aritmética

Maestría en Matemáticas, Dr. en Ciencias
Una secuencia de números \({a_1},\;{a_2},{a_3}, \ldots \) es llamada una progresión aritmética si la diferencia entre dos números consecutivos es igual a un mismo número \(d\), es decir si:
\({a_{n + 1}} - {a_n} = d\)
El número \(d\) es llamado la diferencia de la progresión aritmética.
El elemento \({a_1}\) es llamado el primer elemento de la progresión aritmética.
Los elementos de la progresión aritmética se pueden expresar en términos del primer elemento y de su diferencia, es decir:
\({a_1},{a_1} + d,{a_1} + 2d,{a_1} + 3d\)
Son los primeros cuatro elementos de la progresión aritmética; en general, el \(k – \)ésimo elemento queda expresado de la siguiente manera:
\({a_k} = {a_1} + \left( {k – 1} \right)d\)
de la expresión anterior se obtiene:
\({a_k} – {a_l} = {a_1} + \left( {k – 1} \right)d – \left( {{a_1} + \left( {l – 1} \right)d} \right)\)
\({a_k} – {a_l} = \left( {k – l} \right)d\)
La expresión anterior es equivalente a:
\({a_k} = {a_l} + \left( {k – l} \right)d\)
Ejemplos aplicados para progresión aritmética
1. Hallar la diferencia de la progresión aritmética: \(3,8,13,18, \ldots \) y encontrar los elementos \({a_{20}},\;{a_{99}}\)
Solución
Como \(5 = 8 – 3 = 13 – 8 = 18 – 3\) podemos concluir que la diferencia es:
\(d = 5\)
\({a_{20}} = {a_1} + \left( {20 – 1} \right)d = 3 + 19\left( 5 \right) = 98\)
\({a_{99}} = {a_1} + \left( {99 – 1} \right)d = 3 + 98\left( 5 \right) = 493\)
2. En una progresión aritmética se tiene: \({a_{17}} = 20\;\)y \({a_{29}} = – 130\), determinar la diferencia de la progresión aritmética y escribir los primeros 5 elementos.
Solución
Usando
\({a_k} – {a_l} = \left( {k – l} \right)d\)
\({a_{29}} – {a_{17}} = \left( {29 – 17} \right)d\)
\( – 130 – 20 = \left( {12} \right)d\)
\( – 150 = \left( {12} \right)d\)
\(12d = – 150\)
\(d = – \frac{{150}}{{12}} = – \frac{{25}}{2}\)
Para encontrar los primeros 5 elementos; calcularemos \({a_1}\):
\({a_k} = {a_1} + \left( {k – 1} \right)d\)
\({a_{17}} = {a_1} + \left( {17 – 1} \right)\left( { – \frac{{25}}{2}} \right)\)
\(20 = {a_1} + \left( {16} \right)\left( { – \frac{{25}}{2}} \right)\)
\(20 = {a_1} – 200\)
\({a_1} = 20 + 200 = 220\)
Los primeros 5 elementos son:
\(220,220 + \left( { – \frac{{25}}{2}} \right),220 + 2\left( { – \frac{{25}}{2}} \right),220 + 3\left( { – \frac{{25}}{2}} \right),220 + 4\left( { – \frac{{25}}{2}} \right)\)
\(220,\frac{{415}}{2},195,\frac{{365}}{2},170\)
Números poligonales y la suma de los primeros \(n\) elementos de una progresión aritmética
Números triangulares
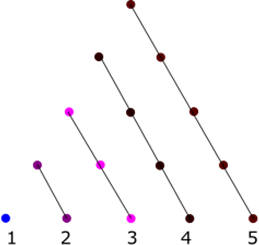
Los números triangulares \({T_n}\;\)se forman a partir de la progresión aritmética: \(1,2,3,4 \ldots \); de la siguiente manera.
\({T_1} = 1\)
\({T_2} = 1 + 2 = 3\)
\({T_3} = 1 + 2 + 3 = 6\)
\({T_4} = 1 + 2 + 3 + 4 = 10\)
Números cuadrados
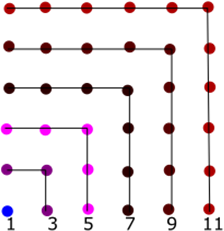
Los números cuadrados \({C_n}\;\)se forman a partir de la progresión aritmética: \(1,3,5,7 \ldots \); de la siguiente manera
\({C_1} = 1\)
\({C_2} = 1 + 3 = 4\)
\({C_3} = 1 + 3 + 5 = 9\)
\(C{\;_4} = 1 + 3 + 5 + 7 = 16\)
Números pentagonales
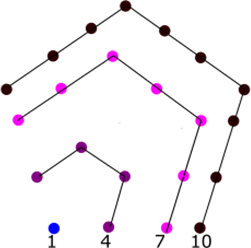
Los números cuadrados \({P_n}\;\)se forman a partir de la progresión aritmética: \(1,3,5,7 \ldots \); de la siguiente manera
\({P_1} = 1\)
\({P_2} = 1 + 4 = 5\)
\({P_3} = 1 + 4 + 7 = 12\)
\({P_4} = 1 + 4 + 7 + 10 = 22\)
A continuación, mostraremos la fórmula para encontrar la suma de los primeros \(n\) elementos de una progresión aritmética.
Dada la progresión aritmética, \({a_1},{a_2} = {a_1} + d,{a_3} + 2d, \ldots .,{a_n} = {a_1} + \left( {n – 1} \right)d\). Para calcular la suma \({S_n} = {a_1} + {a_2} + {a_3} + \ldots + {a_n};\) se puede usar la fórmula:
\({S_n} = \frac{{n\left( {{a_1} + {a_n}} \right)}}{2}\)
La cual es equivalente a
\({S_n} = \frac{{n\left( {2{a_1} + \left( {n – 1} \right)d} \right)}}{2}\)
Aplicando la fórmula anterior, se obtienen las fórmulas para calcular los números triangulares, cuadrados y pentagonales; las cuales se muestran en la siguiente tabla.
| Número poligonal | \({a_1}\) | \(d\) | Fórmula |
|---|---|---|---|
| Triangular \(n – \)ésimo | 1 | 1 | \({T_n} = \frac{{n\left( {n + 1} \right)}}{2}\) |
| Cuadrado \(n – \)ésimo | 1 | 2 | \({C_n} = {n^2}\) |
| Pentagonal \(n – \)ésimo | 1 | 3 | \({P_n} = \frac{{n\left( {3n – 1} \right)}}{2}\) |
Ejemplo sobre números poligonales
3. Del ejemplo 2 calcular \({S_{33}}\).
Solución
En este caso \({a_1} = 200\) y \(d = – \frac{{25}}{2}\)
Aplicando
\({S_n} = \frac{{n\left( {2{a_1} + \left( {n – 1} \right)d} \right)}}{2}\)
\({S_{33}} = \frac{{34\left( {2\left( {200} \right) + \left( {33 – 1} \right)\left( { – \frac{{25}}{2}} \right)} \right)}}{2}\)
\({S_{33}} = 17\left( {400 + 16\left( { – 25} \right)} \right) = 17\left( 0 \right) = 0\)
Medios aritméticos
Dados dos números \(a\;\)y \(b,\) los números \({a_2},{a_3}, \ldots ,{a_{k + 1}}\) son llamados \(k\) medios aritméticos de los números \(a\;\)y \(b\); si la secuencia \(a,{a_2},{a_3}, \ldots ,{a_{k + 1}},b\) es una progresión aritmética.
Para saber los valores de los \(k\) medios aritméticos de los números \(a\;\)y \(b\), basta con conocer la diferencia de la progresión aritmética, para ello hay que considerar, lo siguiente:
\(a = {a_1},{a_2},{a_3}, \ldots ,{a_{k + 1}},{a_{k + 2}} = b,\)
de lo anterior establecemos la relación:
\(b = a + \left( {k + 2 – 1} \right)d\)
Al despejar \(d\), se obtiene:
\(d = \frac{{b – a}}{{k + 1}}\)
Ejemplos
4. Hallar 7 medias aritméticas entre los números -5 y 25.
Solución
Al aplicar
\(d = \frac{{b – a}}{{k + 1}}\)
con \(b = 25,\;a = – 5\) y \(k = 7\;\):
\(d = \frac{{25 – \left( { – 5} \right)}}{{7 + 1}} = \frac{{30}}{8} = \frac{{15}}{4}\)
Las 7 medias aritméticas son:
\( – \frac{5}{4},\;\frac{5}{2},\;\frac{{25}}{4},10,\frac{{55}}{4},\frac{{35}}{2},\frac{{85}}{4}\)
9. Una persona, para comprar un refrigerador, dio $2000, como enganche y el resto lo pagó con su tarjeta de crédito a 18 meses sin intereses. Al mes debe pagar $550 al mes para saldar la deuda, que adquirió para pagar su refrigerador.
a. ¿Cuál es el costo del refrigerador?
b. En caso de haber pagado el resto a 12 meses sin intereses, de cuánto sería la mensualidad.
Solución
a. En este caso:
\({a_{19}} = 2000 + 18\left( {550} \right)\)
\({a_{19}} = 2000 + 9900 = 11900\)
b. Entre los números 2000 y 11900 debemos encontrar 11 medias aritméticas, por lo cual:
\(d = \frac{{11900 – 2000}}{{12}} = 825\)
5. Dada la secuencia \(7,\;22,\;45,\;76,115,162\) encontrar los siguientes 3 elementos y la expresión general del elemento \(n\).
Solución
La secuencia en cuestión no es una progresión aritmética, pues \(22 – 7 \ne 45 – 22\) , pero podemos formar una secuencia con las diferencias de dos elementos consecutivos y la siguiente tabla muestra los resultados:
| Elementos de la secuencia \({b_n}\) | Secuencia \(\;{c_n} = {b_n} – {b_{n – 1}}\) | \(d = {c_{n + 1}} – {c_n}\) |
|---|---|---|
| \({b_1} = 7\) | \({c_1} = {b_1}\) | |
| \({b_2} = 22\) | \({c_2} = {b_2} – {b_1} = 15\) | \({c_2} – {c_1} = 8\) |
| \({b_3} = 45\) | \({c_3} = {b_3} – {b_2} = \)23 | \({c_3} – {c_2} = 8\) |
| \({b_4} = 76\) | \({c_4} = {b_4} – {b_3} = 31\) | \({c_4} – {c_3} = 8\) |
| \({b_5} = 115\) | \({c_5} = {b_5} – {b_4} = 39\) | \({c_5} – {c_4} = 8\) |
| \({b_6} = 162\) | \({c_6} = {b_6} – {b_5} = 47\) | \({c_6} – {c_5} = 8\) |
La tercera columna de la tabla anterior nos indica que la secuencia \(15,\;23,31,39,\;47, \ldots .\); es una secuencia aritmética cuya diferencia es \(d = 8\).
A continuación, escribiremos a los elementos de la secuencia \({b_n}\) en términos de la secuencia \({c_n},\)
\({b_1} = {c_1}\)
\({b_2} = {c_1} + {c_2}\)
\({b_3} = {b_2} + {c_3} = {c_1} + {c_2} + {c_3}\)
\({b_4} = {b_3} + {c_4} = {c_1} + {c_2} + {c_3} + {c_4}\)
En general se tiene:
\({b_n} = {c_1} + {c_2} + {c_3} + \ldots + {c_n}\;\)
Al aplicar
\({S_n} = \frac{{n\left( {2{c_1} + \left( {n – 1} \right)d} \right)}}{2}\)
Con \({c_1} = 7\) y \(d = 8,\) obtenemos:
\({b_n} = \frac{{n\left( {14 + \left( {n – 1} \right)8} \right)}}{2}\)
\({b_n} = n\left( {7 + 4\left( {n – 1} \right)} \right)\)
\({b_n} = n\left( {4n + 3} \right)\)
Al aplicar la fórmula anterior: \({b_7} = 217,\;{b_8} = 280,\;{b_9} = 351\)

Trabajo publicado en: Nov., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.