Significado de teoremas de Tales Definición, ilustración, y ejemplos

Licenciada en Física
Definición formal
El primero de los dos teoremas de Tales asevera que cuando varias rectas paralelas cortan a un par de rectas cualesquiera L1 y L2, los segmentos que se forman entre las paralelas sobre una de dichas rectas, son directamente proporcionales a los segmentos correspondientes sobre la otra recta.
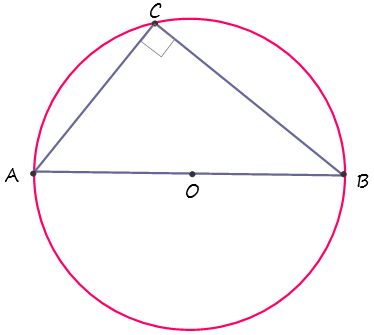
El segundo teorema responde a una circunferencia cuyo centro es O, y sobre la que se identifican tres puntos de pertenencia, determinadas como A, B y C, exponiendo el segmento AC como diámetro. Respecto a un triángulo con vértices en A, B y C, afirma que existe un ángulo recto (90º) entre los segmentos AB y BC, por lo que el triángulo ABC es rectángulo.
Ilustración del primer Teorema de Tales
La disposición se muestra en el siguiente gráfico, con L1 y L2 de color azul e intersectadas por las rectas paralelas de color rojo. Sobre la recta L1 se forman los segmentos AB, BC y CD, mientras que sobre la recta L2 quedan determinados los segmentos A’B’, B’C’ y C’D’.
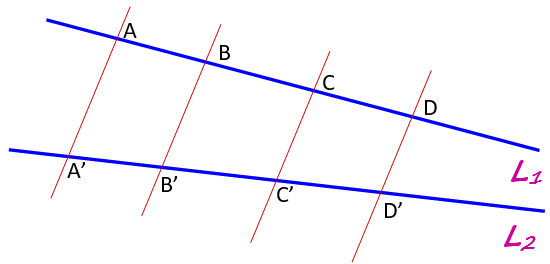
El teorema de Tales afirma la siguiente igualdad entre los cocientes o razones entre las longitudes de estos segmentos:
\(\frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CD}{C’D’}\)
Y también es válido para segmentos más largos, como:
\(\frac{AC}{A’C’}=\frac{AD}{A’D’}=\frac{BD}{B’D’}\)
Ilustración del segundo Teorema de Tales
La situación se esquematiza en la figura:
El filósofo y matemático griego de la antigüedad Tales de Mileto (624-546 aC) no dejó obras escritas, que se sepa. Sin embargo, es considerado uno de los Siete Sabios de la antigua Grecia y fue el primero en comprobar teoremas relativos a la geometría y establecer algunos nuevos, por eso, junto a Euclides, se le considera como el padre de esta disciplina.
Se cuentan muchas historias acerca de Tales, como que fue capaz de calcular la altura de la Gran Pirámide de Giza, midiendo las longitudes de las sombras proyectadas por él mismo y por la pirámide sobre el suelo del desierto. Para ello supuso que los rayos del Sol inciden paralelamente sobre los objetos.
También tuvo la habilidad de averiguar cómo medir la distancia que hay entre un barco en el mar y un punto en la costa, mediante triangulación.
El teorema de Tales y los triángulos
El primer teorema de Tales no solo se aplica a dos rectas paralelas, sino también a los triángulos, algo que lo hace aún más interesante.
Para verlo, considérense los triángulos ABC y A’B’C’, que tienen un ángulo común, cuyo vértice está en el punto A = A’. Además, los lados BC y B’C’ son paralelos.
Dos triángulos que cumplen con estas condiciones se dice que son triángulos en posición de Tales. Lo importante de esto es que los triángulos en posición de Tales son semejantes, por lo que guardan proporcionalidad en sus lados y sus ángulos internos tienen la misma medida.
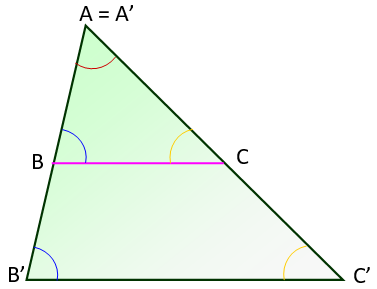
Matemáticamente, establece que la proporcionalidad en los segmentos así formados se exprese de este modo:
\(\frac{A’B’}{A’C’}=\frac{AB}{AC}=\frac{BB’}{CC’}\)
Y como los triángulos son semejantes, dicha proporcionalidad entre los lados de ambos triángulos queda así:
\(\frac{A’B’}{AB}=\frac{A’C’}{AC}=\frac{B’C’}{BC}\)
Seguidamente se aplica el teorema para determinar las longitudes desconocidas en un triángulo.
Ejemplos prácticos para explicar ambas definiciones
Ejemplo 1: Calcular, mediante el teorema de Tales, las longitudes denotadas como “x” e “y” que aparecen en la siguiente figura
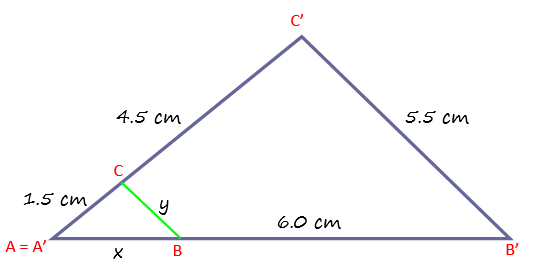
El lado “y” es paralelo al lado que mide 5.5 cm, por lo tanto, se tienen dos triángulos en posición de Tales, que son semejantes: ABC y A’B’C’. Hay que identificar cuidadosamente los lados, para aplicar el teorema correctamente.
El triángulo ABC, más pequeño, tiene lados:
. AB = x
. AC = 1.5 cm
. CB = y
Mientras que los lados del triángulo mayor A’B’C’ son:
. A’B’= x + 6.0 cm
. C’B’= 5.5 cm
. A’C’= 1.5 + 4.5 cm = 6.0 cm
Ahora se observa el teorema de Tales para plantear las correspondientes proporcionalidades:
\(\frac{A’B’}{AB}=\frac{A’C’}{AC}=\frac{B’C’}{BC}\)
Sustituyendo los valores disponibles, se transforma en:
\(\frac{x+6.0}{x}=\frac{6.0}{1.5}=\frac{5.5}{y}\)
Ahora se pueden plantear las siguientes ecuaciones:
1) \(\frac{x+6.0}{x}=\frac{6.0}{1.5}=4\)
\(\frac{x+6}{x}=4\)
\(x+6=4x\)
\(4x-x=6\)
\(3x=6\)
x = 2 cm
2) \(\frac{6.0}{1.5}=\frac{5.5}{y}\)
\(4=\frac{5.5}{y}\)
\(4y=5.5\)
y = 1.375 cm
Ejemplo 2: El radio de la circunferencia de la figura es de 4 cm y el segmento BC mide 7.27 cm. Calcular el perímetro del triángulo ABC
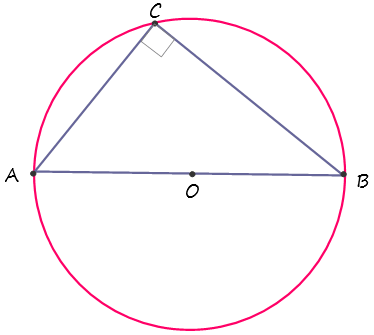
Para calcular el perímetro P se requiere sumar las longitudes de los lados del triángulo:
P = AB + BC + AC
El segmento AB mide 8 cm, ya que coincide con el diámetro de la circunferencia, y el diámetro mide el doble del radio.
El segmento AC es uno de los catetos del triángulo, que es rectángulo, tal como lo asegura el segundo teorema de Tales, por lo tanto, el teorema de Pitágoras es aplicable, con el segmento AB como hipotenusa:
\(AC=\sqrt{A{{B}^{2}}-B{{C}^{2}}}=\sqrt{{{(8cm)}^{2}}-{{(7.27cm)}^{2}}}=3.34cm\)
De esta manera el perímetro del triángulo vale:
P = 3.34 cm + 8.00 cm + 7.27 cm = 18.61 cm

Trabajo publicado en: Mar., 2021.