Ángel Zamora Ramírez
Licenciado en Física

Triangulo Escaleno

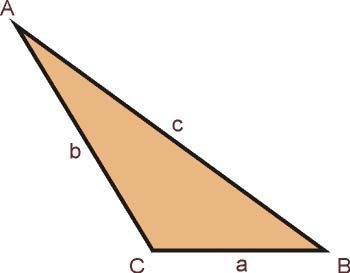Un triángulo escaleno es un tipo de triángulo cuyos lados tienen distintas longitudes y cuyos ángulos también tienen magnitudes diferentes, configurándose como la categoría de triángulo más general que existe, por ello, las relaciones matemáticas que se pueden obtener a partir de esta figura pueden aplicarse a tipos de triángulos más específicos.

Un poco sobre el triángulo rectángulo

Antes de hablar más específicamente sobre el triángulo escaleno es importante hablar del triángulo rectángulo, el cual es un triángulo que cuenta con un ángulo recto, es decir, un ángulo de 90°. Consideremos el siguiente triángulo rectángulo:

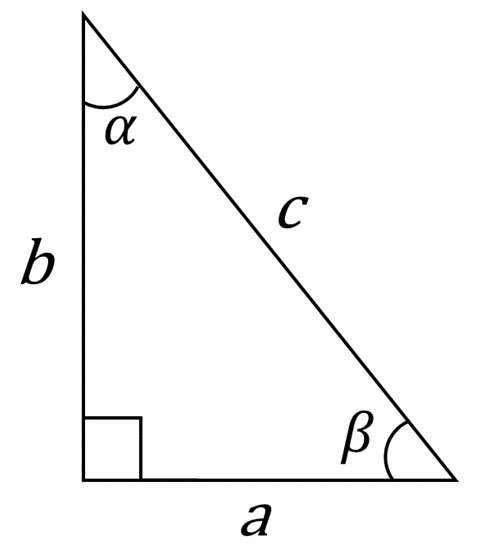
Los lados a y b que forman el ángulo recto se llaman catetos, mientras que el lado c opuesto al ángulo recto se conoce como hipotenusa. De este tipo de triángulo es que se obtiene el famoso Teorema de Pitágoras, que establece la relación que existe entre los catetos y la hipotenusa.

\({c^2} = {a^2} + {b^2}\)

También, de este tipo de triángulo es que surgen las funciones trigonométricas que relacionan los catetos y la hipotenusa de un triángulo rectángulo con los dos ángulos agudos que lo componen.

\(\sin \alpha = \frac{a}{c},\;\;\cos \alpha = \frac{b}{c},\;\;\tan \alpha = \frac{a}{b},\;\;\sin \beta = \frac{b}{c}\;,\;\;\cos \beta = \frac{a}{c}\;,\;\;\tan \beta \; = \frac{b}{a}\)

Triángulo Escaleno: Ley de senos y ley de cosenos

Consideremos la siguiente figura de triángulo escaleno:

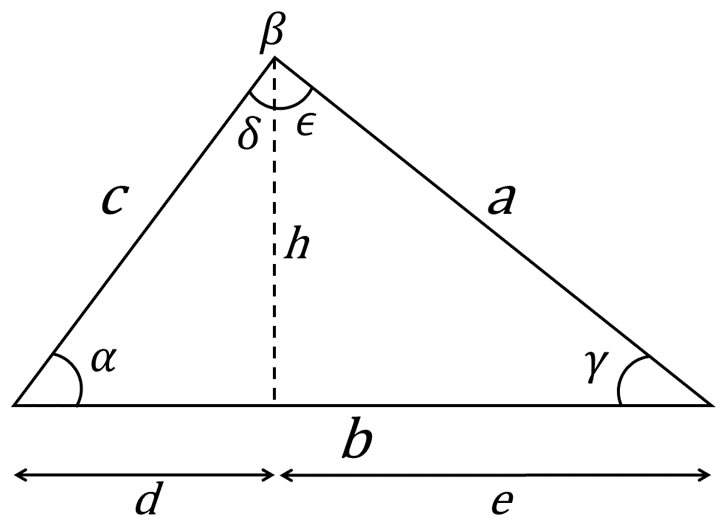
Como vimos, en un triángulo rectángulo existen relaciones matemáticas entre sus lados y sus ángulos, ¿Será que podríamos encontrar unas relaciones parecidas en el triángulo escaleno? Para tratar de responder a esta pregunta trazaremos una línea recta de longitud h que parte desde el vértice que forman los lados a y c, y que incide perpendicularmente sobre el lado b. Al hacer esto el ángulo \(\beta \) queda dividido en dos ángulos \(\delta \) y \(ε\) tal que \(\delta + ε = \beta \), y, además, el lado b también se disecciona en dos segmentos d y e, esto implica que \(d + e = b\). De esta manera acabamos de dividir al triángulo escaleno en dos triángulos rectángulos que ya conocemos perfectamente. Podemos empezar calculando el seno de los ángulos \(\alpha \) y \(\gamma \). Por definición de la función seno tenemos que:

\(\sin \alpha = \frac{h}{c},\;\;\sin \gamma = \frac{h}{a}\)

De ambas ecuaciones podemos despejar el término h, de esta manera obtenemos que:

\(h = c\sin \alpha = a\sin \gamma \)

Reacomodando términos, podemos concluir lo siguiente:

\(\frac{a}{{\sin \alpha }} = \frac{c}{{\sin \gamma }}\)

Ahora, sabemos que \(\beta = \delta + ε\), entonces:

\(\sin \beta = \sin \left( {\delta + ε} \right)\)

Utilizaremos la siguiente fórmula para el seno de una suma de ángulos:

\(\sin \left( {x + y} \right) = \sin x\cos y + \cos x\sin y\)

Aplicando esto para el ángulo \(\beta = \delta + ε\) tenemos:

\(\sin \beta = \sin \left( {\delta + ε} \right) = \sin \delta \cos ε + \cos \delta \sin ε\)

Observando la figura del triángulo escaleno podemos expresar los senos y cosenos de \(\delta \) y \(ε\) en función de los lados de los dos triángulos rectángulos que lo componen. Reemplazando esto en la ecuación anterior obtenemos:

\(\sin \beta = \frac{d}{c}\frac{h}{a} + \frac{h}{c}\frac{e}{a}\)

Previamente, habíamos obtenido que \(\sin \alpha = h/c\) y \(\sin \gamma = h/a\). Sustituimos esto en la ecuación anterior

\(\sin \beta = \frac{d}{c}\sin \gamma + \frac{e}{a}\sin \alpha \)

Anteriormente también concluimos que existe una relación entre las funciones seno de \(\alpha \) y de \(\gamma \) tal que: \(\sin \alpha /a = \sin \gamma /c\). Podemos sustituir uno de estos términos en la ecuación anterior:

\(\sin \beta = \frac{d}{a}\sin \alpha + \frac{e}{a}\sin \alpha \)

Factorizamos el lado derecho de la ecuación

\(\sin \beta = \left( {d + e} \right)\frac{{\sin \alpha }}{a}\)

Sin embargo, sabemos que \(b = d + e\). Reemplazando esto en la ecuación anterior y reacomodando ambos lados podemos decir que:

\(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }}\)

Como ya sabemos también que \(a/\sin \alpha = c/\sin \gamma \), de manera general se tiene entonces que:

\(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \gamma }}\)

Este último resultado se conoce como Ley de senos. Ahora, tratemos de encontrar otra relación útil utilizando el mismo triángulo escaleno. Esta vez calcularemos el coseno del ángulo \(\alpha \) que por definición estaría dado por:

\(\cos \alpha = \frac{d}{c}\)

Despejando para d tendríamos simplemente que:

\(d = c\cos \alpha \)

Recordemos que \(b = d + e\), lo cual implica que \(e = b – d\). Si sustituimos la ecuación anterior en este resultado se tiene:

\(e = b – c\cos \alpha \)

Por otro lado, sabemos por Teorema de Pitágoras q el lado a del triángulo escaleno puede expresarse como:

\({a^2} = {h^2} + {e^2}\)

Y también recordemos que \(\sin \alpha = h/c\), de tal manera que \(h = c\sin \alpha \). Reemplazando esto en la ecuación anterior, así como el resultado previamente obtenido para e, se obtiene que:

\({a^2} = {c^2}{\sin ^2}\alpha + {\left( {b – c\cos \alpha } \right)^2}\)

Desarrollando el binomio al cuadrado del lado derecho de la ecuación obtenemos:

\({a^2} = {c^2}{\sin ^2}\alpha + {b^2} – 2bc\cos \alpha + {c^2}{\sin ^2}\alpha \)

Reagrupando y factorizando término esta última ecuación quedaría como:

\({a^2} = {b^2} + {c^2}\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) – 2bc\cos \alpha \)

Utilizando la identidad \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (Esto es sencillo de demostrar utilizando las definiciones de las funciones seno y coseno), finalmente llegamos a que:

\({a^2} = {b^2} + {c^2} – 2bc\cos \alpha \)

Siguiendo un procedimiento parecido al anterior podemos llegar también a los siguientes resultados:

\({b^2} = {a^2} + {c^2} – 2ac\cos \beta \)

\({c^2} = {a^2} + {b^2} – 2ab\cos \gamma \)

Esto de aquí es lo que se conoce como Ley de cosenos. Tanto la ley de senos como la ley de cosenos son relaciones matemáticas que existen entre los lados y los ángulos que forman un triángulo escaleno. De hechos se podría decir que estas son las relaciones más generales que existen para los lados y los ángulos de cualquier triángulo ya que podemos aplicarlas a tipos más especiales de triángulos. Por ejemplo, supongamos que \(\gamma = 90^\circ \), es decir, el triángulo escaleno con el que trabajamos es ahora un triángulo rectángulo. Como \(\cos 90^\circ = 1\), entonces la ley de cosenos para el lado c en este caso quedaría solamente como:

\({c^2} = {a^2} + {b^2}\).

Lo cual es exactamente el Teorema de Pitágoras para la hipotenusa de un triángulo rectángulo.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Art. actualizado: Enero 2023; sobre el original de noviembre, 2012.

Datos para citar en modelo APA: Zamora Ramírez, A. (Enero 2023). Definición de Triangulo Escaleno. Significado.com. Desde https://significado.com/triangulo-escaleno/