Definición de Afelio y de Perihelio

Ángel Zamora Ramírez
Licenciado en Física

El afelio y el perihelio son dos puntos que pertenecen a la órbita de un planeta alrededor del Sol. El afelio es el punto que corresponde a la distancia máxima que alcanza el planeta con respecto al Sol. Por el contrario, el perihelio, también denominado perigeo, es el punto en el que dicho planeta se encuentra a una distancia mínima del Sol.

Las órbitas que trazan los planetas en su movimiento de traslación son elípticas y el Sol se encuentran en uno de los focos de la elipse. Esta peculiaridad del movimiento planetario hace que la distancia que existe entre un planeta y el Sol no sea siempre la misma. Hay dos puntos en los que un planeta en su trayectoria alrededor del Sol se encuentra a una distancia máxima y a una distancia mínima de este, estos puntos se conocen como “afelio” y “perihelio”, respectivamente.

Primera Ley de Kepler: Las órbitas son elípticas

Hacia el siglo XVI ocurrió una de las grandes revoluciones en la historia de la ciencia y fue la publicación del modelo heliocéntrico de Copérnico. Nicolás Copérnico fue un matemático y astrónomo polaco que tras años de estudio y de investigación en Astronomía Matemática llegó a la conclusión de que la Tierra y el resto de planetas se movían a lo largo de trayectorias circulares alrededor del Sol.

Este modelo heliocéntrico de Copérnico no solo desafiaba al modelo geocéntrico de Ptolomeo y a siglos de observaciones y mediciones, sino que también desafiaba a una tradición antropocentrista instaurada por la iglesia católica. Esto último hizo que Copérnico afirmara que su modelo era sólo una estrategia para determinar con mejor precisión la posición de los astros en la bóveda celeste pero que no era una representación de la realidad. A pesar de ello la evidencia era clara y su modelo heliocéntrico llevó a una revolución copernicana que cambió la Astronomía para siempre.

Durante ese mismo siglo, el astrónomo danés Tycho Brahe realizó mediciones muy precisas de la posición de los planetas y de otros cuerpos celestes. Durante su trayectoria, Tycho Brahe invitó al matemático alemán Johannes Kepler a trabajar junto con él en sus investigaciones, cosa que fue aceptada por Kepler. Brahe era demasiado celoso con los datos que había recopilado, por lo que el acceso que tenía Kepler a ellos era muy limitado. Además, Brahe trataba a Kepler como su subordinado, cosa que a este último no le agradó del todo y la relación entre ellos fue complicada.

Tras la muerte de Tycho Brahe en 1601, Kepler se adueñó de sus preciados datos y de sus observaciones antes de que fueran reclamadas por los herederos. Kepler estaba consciente que Brahe carecía de los herramientas analíticas y matemáticas para comprender el movimiento planetario a partir de sus observaciones. Fue así que el minucioso estudio de los datos de Brahe por parte de Kepler dio respuesta a varias preguntas que se tenían con respecto al movimiento planetario.

Kepler estaba totalmente convencido que el modelo heliocéntrico de Copérnico era el correcto, sin embargo, había algunas discrepancias con la posición aparente que tenían los planetas en la bóveda celeste a lo largo del año. Tras analizar detenidamente los datos recolectados por Brahe, Kepler se dio cuenta que las observaciones encajaban mejor con un modelo heliocéntrico en el que los planetas trazan órbitas elípticas alrededor del Sol, y no órbitas circulares como lo propuso Copérnico. Esto se conoce como la “Primera Ley de Kepler” y fue publicada junto con la Segunda Ley de Kepler en el año 1609 en su obra “Astronomía Nova”.

Para entender mejor esto tenemos que entender primero la definición y la estructura de una elipse. Una elipse se define como una curva cerrada cuyos puntos que la forman satisfacen que la suma de las distancias entre estos y otros puntos llamados “focos” es siempre la misma. Consideremos la siguiente elipse:

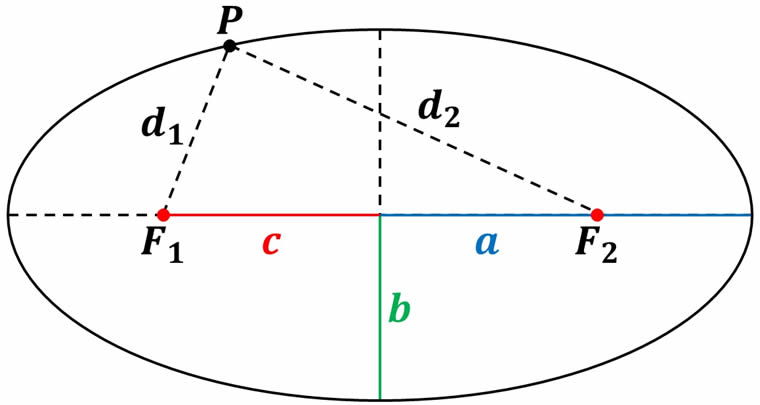
En esta elipse los puntos \({F_1}\) y \({F_2}\) son los denominados “focos”. Una elipse tiene dos ejes de simetría que son perpendiculares entre sí y que se interceptan en el centro de esta. La longitud \(a\) se llama “semieje mayor” y corresponde a la distancia entre el centro de la elipse y el punto extremo de esta que se encuentra a lo largo del eje de simetría mayor. De igual manera, la longitud \(b\) conocida como “semieje menor” es la distancia entre el centro de la elipse y el punto extremo de esta ubicado a lo largo del eje de simetría menor. A la distancia \(c\) que existe entre el centro de la elipse y cualquiera de sus focos se le conoce como “semidistancia focal”.

Por su propia definición, si tomamos cualquier punto \(P\) que pertenece a la elipse y trazamos la distancia \({d_1}\) entre el punto \(P\) y el foco \({F_1}\), y otra distancia \({d_2}\) entre el punto \(P\) y el otro foco \({F_2}\), estas dos distancias satisfacen:

\({d_1} + {d_2} = 2a\)

Lo cual es válido para cualquier punto de la elipse. Otra magnitud que podemos mencionar es la “excentricidad” de la elipse la cual está denotada por la letra \(\varepsilon \) y determina que tan achatada está la elipse. La excentricidad está dada por:

\(\varepsilon = \frac{c}{a}\;;\;0 \le \varepsilon \le 1\)

Con todo esto en nuestras manos, podemos hablar ahora sí de las órbitas elípticas de los planetas alrededor del Sol. Un esquema un tanto exagerado de la órbita de un planeta alrededor del Sol sería el siguiente:

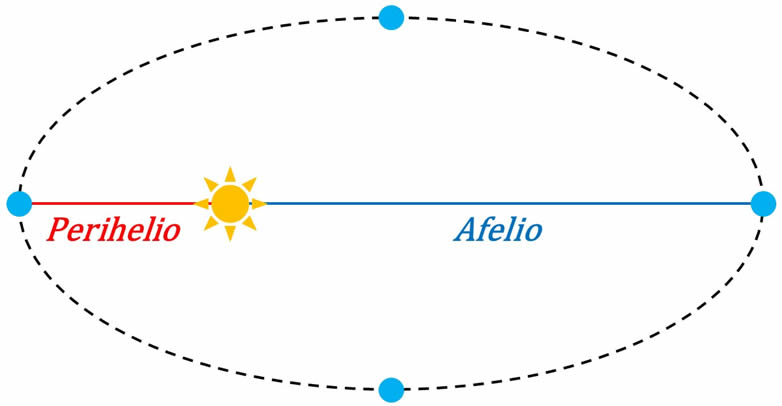
En este esquema podemos darnos cuenta de que el Sol se encuentra en uno de los focos de la órbita elíptica del planeta. El perihelio (\({P_h}\)) será la distancia dada por:

\({P_h} = a – c\)

Por otro lado, el afelio (\({A_f}\)) será la distancia:

\({A_f} = a + c\)

O bien, ambas distancias en términos de la excentricidad de la órbita serán:

\({P_h} = \left( {1 – \varepsilon } \right)a\)

\({A_f} = \left( {1 + \varepsilon } \right)a\)

Las órbitas planetarias, al menos en nuestro Sistema Solar, tienen una excentricidad muy pequeña. Por ejemplo, la órbita de la Tierra tiene una excentricidad aproximada de \(\varepsilon \approx 0.017\). El semieje mayor de la órbita terrestre es de alrededor de \(a \approx 1.5 \times {10^8}\;km\). Con todo lo mencionado anteriormente podemos calcular que el perihelio y el afelio de la Tierra serán: \({P_h} \approx 1.475 \times {10^8}\;km\) y \({A_f} \approx 1.525 \times {10^8}\;km\).

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Oct., 2023.

Datos para citar en modelo APA: Zamora Ramírez, A. (octubre, 2023). Definición de Afelio y de Perihelio. Significado.com. Desde https://significado.com/afelio-perihelio/