Significado de leyes de Kepler Definición, y explicación de la primera, segunda y tercera ley

Licenciada en Física
Definición formal
Las leyes de Kepler son un hallazgo del astrónomo alemán Johannes Kepler (1571-1630) que revela los fundamentos de la cinemática de los cuerpos celestes.
Kepler las dedujo partiendo de los datos recolectados por su maestro, el danés Tycho Brahe (1546-1601). Cerca del final de su vida, Brahe estuvo al servicio del emperador Rodolfo II del Sacro Imperio, y había instalado un sofisticado observatorio en las cercanías de Praga, hacia 1599. Para entonces ya tenía una gran cantidad de datos astronómicos que había recabado, y sin la ayuda del telescopio, ya que para la fecha no se había inventado todavía.
Brahe contrató a Kepler, quien entonces era profesor de matemáticas en Austria, como su asistente. Y Kepler finalmente heredaría los datos del sabio danés, al fallecer este poco tiempo después, en 1601. Tardó ocho años en analizar los datos de su mentor, hasta que en 1609 publicó sus dos primeras leyes. Diez años después, en 1619, dio a conocer el hallazgo de la tercera.
Hasta el día de hoy, las tres leyes de Kepler, fruto de una ardua labor, siguen siendo la base del movimiento, no solo de los planetas alrededor del Sol, sino de los demás cuerpos del Sistema Solar, incluyendo satélites naturales y artificiales, y al movimiento de estos respecto a su planeta padre.
Explicación de la Primera ley de Kepler
Inicialmente, Kepler observó que las órbitas planetarias no eran circunferencias del todo perfectas, tal era la precisión de las medidas hechas por Brahe. De esta forma logró establecer que:
“Cada planeta en el Sistema Solar gira en torno al Sol siguiendo una órbita de forma elíptica, con la estrella ubicada uno de los focos”.
A esta ley se la conoce como la “ley de las órbitas”, por razones obvias.
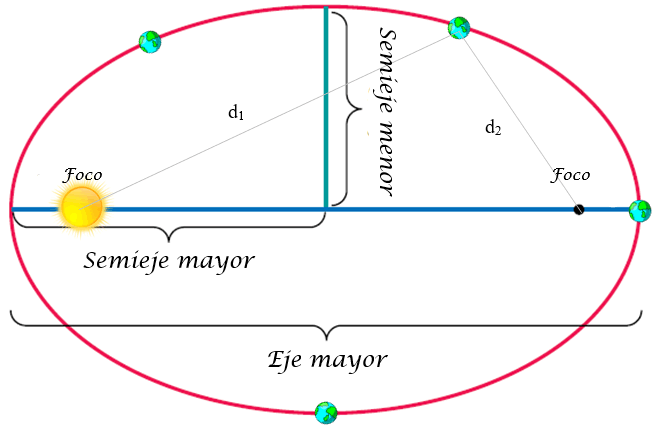
Una elipse es una curva cerrada como se muestra en la siguiente figura. Cualquier punto sobre la elipse cumple la condición de que la suma de sus respectivas distancias a los focos es constante (ver figura):
\({{d}_{1}}+{{d}_{2}}=cons\tan te\)
El eje mayor de la elipse pasa por su centro y por ambos focos, mientras que el eje menor es perpendicular al eje mayor y también pasa por el centro. El semieje mayor es la mitad de la medida del eje mayor, y es la magnitud que se usa para describir matemáticamente a la elipse, junto al semieje menor, que es la mitad del eje menor.
El grado de alargamiento de la elipse se mide a través de la excentricidad “e”, un valor comprendido entre 0 y 1 que se obtiene del cociente entre la distancia foco-centro “c” y el semieje mayor “a”:
e = c / a
Cuando la excentricidad vale 0, significa que la distancia foco-centro “c” también es nula, por lo tanto los focos se ubican en el centro y simplemente se tiene una circunferencia. Una excentricidad grande, en cambio, señala una elipse muy alargada, con los focos distantes del centro.
En realidad, las excentricidades de las órbitas de los planetas mayores del Sistema Solar son muy pequeñas, pudiendo imaginarse la minuciosidad con la que Brahe debió tomar sus medidas, y la habilidad con la que Kepler supo extraer de ellas el secreto de los movimientos planetarios.
Explicación de la Segunda ley de Kepler
La segunda ley de Kepler, alternativamente llamada “ley de las áreas”, es una consecuencia de la conservación del momento angular. Hace referencia a la velocidad de los planetas al recorrer la órbita elíptica, cuando establece que:
“La línea que une al Sol con cualquiera de los planetas recorre áreas iguales en tiempos iguales”.
En la siguiente figura, que no está a escala, las secciones de color azul tienen áreas iguales y se cubren en el mismo lapso de tiempo.
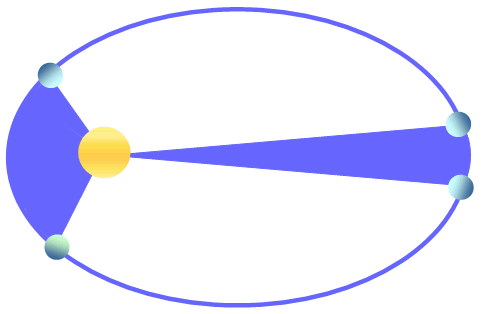
Ahora bien, de la figura se ve que cuando el planeta está más cerca del Sol recorre un arco más grande que cuando está más lejos. Pero la segunda ley afirma que dichos arcos se recorren en tiempos iguales, por lo tanto la conclusión es que el planeta tiene una velocidad instantánea mayor cuando está más cerca esté del Sol, con su máximo en el perihelio (punto más cercano al Sol) y la mínima en el afelio (punto más alejado del Sol).
Tiene sentido, pues la fuerza de atracción gravitatoria ejercida por el Sol aumenta a medida que el planeta se acerca al astro rey, y con ella su velocidad.
Dado que Kepler afirma que se barren áreas iguales en tiempos iguales, se define una magnitud llamada “velocidad areolar”, que representa el área barrida por unidad de tiempo, la cual sí se mantiene constante para un planeta determinado.
Explicación de la Tercera ley de Kepler
La tercera y última ley de Kepler, dada a conocer en 1619, establece el período de la órbita planetaria, que es el tiempo que le toma al planeta recorrerla, razón por la cual se la llama “ley de los períodos”.
En palabras, la tercera ley se expresa de esta manera:
“El período de un planeta dado, al ser elevado al cuadrado, es directamente proporcional al semieje mayor de la órbita elevado al cubo”
Sea T el período del planeta en cuestión y sea “a” la longitud del semieje mayor de su trayectoria elíptica, matemáticamente lo anterior se puede escribir como:
\({{T}^{2}}\propto {{a}^{3}}\)
\({{T}^{2}}=k\cdot {{a}^{3}}\)
La constante de proporcionalidad “k” involucra la masa del sol M, la del planeta m y la constante de gravitación universal G, ya que esta ley en realidad se deriva de la ley de gravitación universal, descubierta por Isaac Newton tiempo después de los hallazgos de Kepler:
\({{T}^{2}}=\text{ }\left[ \frac{\text{4}{{\pi }^{\text{2}}}}{\text{G(M}+\text{m)}} \right]{{a}^{3}}\)
Como la masa M del Sol es mucho mayor que la de cualquier otro cuerpo del Sistema Solar, la expresión anterior se puede aproximar a:
\({{T}^{2}}=\text{ }\frac{\text{4}{{\pi }^{\text{2}}}}{\text{G}\cdot \text{M}}{{a}^{3}}\)
Nótese que el período del planeta no depende de su masa, sino de la longitud del semieje mayor de la elipse que describe alrededor del Sol. Por eso cuanto más lejano se encuentra el planeta del Sol, más tiempo le toma recorrer su órbita.
Esta aproximación no conviene cuando lo que se quiere es aplicar la tercera ley de Kepler a un sistema como la Tierra y la Luna, o el de Plutón y su satélite Caronte, ya que en este caso las masas son comparables.

Trabajo publicado en: Abr., 2021.