¿Qué es el Análisis de Regresión, y cómo se lo define?

Marcoantonio Villanueva Bustamante
Doctor en Psicología

El análisis de regresión es posiblemente la técnica estadística multivariada más empleada para determinar la relación entre una, o un grupo, de variables independientes y una dependiente a modo de que las primeras puedan predecir el cambio en la segunda-

De manera casi innata, los seres humanos tratamos de dar explicaciones a los sucesos que acontecen de manera cotidiana, “esa persona fuma porque se siente estresada”, “comer en exceso conduce a un mayor peso corporal”; sin embargo, sabemos que las explicaciones que damos a tales eventos no siempre son correctas. Daniel Kahneman en su libro “pensar rápido, pensar despacio” describe cómo, aunque las personas tienden a hacer uso de todos los elementos cognoscitivos que poseen, siempre cometerán errores al tratar de explicar algún suceso, lo cual es completamente normal en una realidad donde coexisten múltiples factores de por medio. Entonces, ¿cómo podríamos tratar de explicar sucesos de la manera más certera posible? En las ciencias sociales y de la salud es posible realizar esto mediante el análisis de datos; el cual es definido como conjunto de procedimientos que se ayudan de técnicas estadísticas descriptivas e inferenciales para así extraer información de una muestra empírica de datos y elaborar conclusiones. Dentro del análisis de datos, la técnica que nos permitirá dar explicaciones fiables a sucesos es una técnica multivariada llamada Análisis de Regresión.

El análisis de regresión posee una serie de variantes como el análisis de regresión lineal, análisis de regresión múltiple, análisis de regresión logística, análisis de mediación, análisis de moderación e incluso se podría considerar a los modelos de ecuaciones estructurales (SEM). Sin embargo, todas estas variantes siguen la misma lógica operativa, una o más variables de entrada, que pueden ser conocidas como predictores, variables independientes, variables explicativas o variables antecedentes, predicen la mayor cantidad posible de varianza de una variable de salida, que puede ser conocida como variable dependiente o simplemente criterio; cuando es más de una Variable Independiente, el análisis de regresión también determina cuál de estas tiene mayor influencia en la Variable Dependiente.

Para comprender cómo se produce estas relaciones, se debe recurrir a la siguiente ecuación, la cual nos presenta un modelo de regresión lineal simple:

y = B_o + B_i X e

Donde,
B_o = Origen de la pendiente
B_i = Grado de inclinación de la recta (pendiente)
X = Valor de la VI
e = Residuales (error)

Dicho de una manera sumamente sencilla, esta ecuación indica el grado en la presencia de un predictor (variable independiente) produce un cambio en el criterio (variable dependiente). Es necesario mencionar que aunque la ecuación menciona el residual (error) este no es estimado dentro del modelo, elemento por el cual esta técnica puede ser criticada, pero que su “evolución” los modelos de ecuaciones estructurales (SEM) compensa.

Una vez estimada la ecuación puede ser visualizada mediante el siguiente plano bidimensional, llamado recta de regresión.

Recta o pendiente de regresión

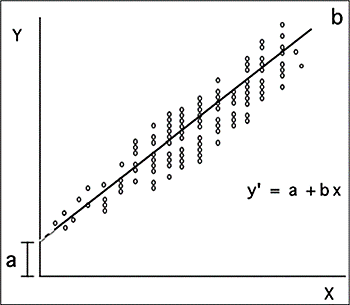
Fuente: Dagnino (2014)

Esta gráfica, además de presentar la relación de las variables involucradas (mediante la nube de puntos), expone una línea que le da el nombre a este diagrama y que indica el grado en que los datos empíricos se ajustan al valor de la regresión (el valor de B).

A pesar de que B nos indica el grado de la pendiente, en realidad no es muy útil para la interpretación debido a que se encuentra expresada en la misma métrica de las variables y, por tanto, sus valores pueden ser demasiados extensos. De este modo, mediante la estandarización de B en función de los Puntajes Z, se obtiene el coeficiente beta (β), cuyos valores pueden encontrarse entre 0 y 1, tanto positivo como negativo y que permite su interpretación. Así, un valor negativo de beta indicará que la variable predictora predice negativamente al criterio, es decir, a mayor presencia del predictor es menos probable la presencia del criterio; por el contrario, una beta positiva indica que la presencia del predictor favorece la presencia del criterio.

Al igual que otras técnicas estadísticas inferenciales, la interpretación de una regresión dependerá del contraste de hipótesis, o bien, del valor de significancia (p), el cual en ciencias sociales típicamente es de p > .05.

Finalmente, un concepto elemental del análisis de regresión es el valor de R2 el cual se refiere a la varianza explicada por el modelo de regresión, el cual puede ser interpretado de forma directa o bien, multiplicándolo por 100 para así conseguir el porcentaje de varianza explicada.

Regresión logística

Tal como se mencionó al inicio, existen diferentes análisis de regresión. Previamente, se abordó la regresión lineal simple y múltiple, estas suponen que tanto las variables predictoras como el criterio son continuas. Sin embargo, cuando las variables no son continuas, es decir, son categóricas, se debe recurrir al análisis de regresión logística, siendo esta la única diferencia con el resto de modelos de regresión.

Por: Marcoantonio Villanueva Bustamante. Licenciado en Psicología, egresado de la Facultad de Psicología de la UNAM, México. Doctor en Psicología por la UFRO, Chile. Actualmente, es investigador independiente que forma parte de diversos equipos de investigación en México y Chile.

Art. actualizado: Sep. 2023; sobre el original de septiembre, 2023.

Datos para citar en modelo APA: Villanueva Bustamante, M. (Sep. 2023). Definición de Análisis de Regresión. Significado.com. Desde https://significado.com/analisis-regresion/