Significado de capacitores en serie y en paralelo Definición, características, y ejercicio

Licenciada en Física
Definición formal
Los capacitores en serie y en paralelo son formas de conexión que posibilitan trabajar con capacitadores en un circuito eléctrico. Cuando se tienen varios capacitores conectados de una u otra forma, es posible encontrar la capacidad equivalente de la combinación mediante operaciones puntuales.
Para facilitar la visualización de las conexiones, los elementos de circuito se tienen representaciones sencillas. En el caso del condensador, el símbolo usado con más frecuencia consiste en dos líneas paralelas de la misma longitud, que pueden estar dispuestas horizontal o verticalmente:
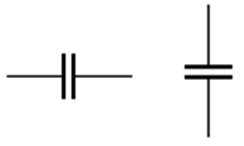
Mientras que las fuentes o baterías necesarias para suministrar corriente continua se representan con dos líneas paralelas de distinta longitud, con el trazo más largo correspondiendo al polo positivo:
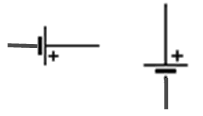
Características de los capacitores en serie
Si se tienen tres capacitores inicialmente descargados y conectados uno después del otro, como se muestra en la figura, esta configuración corresponde a capacitores o condensadores en serie con una batería V. Esta se encarga de suministrar la carga desde el polo positivo, hasta la placa izquierda del capacitor C1, que también adquiere carga positiva.
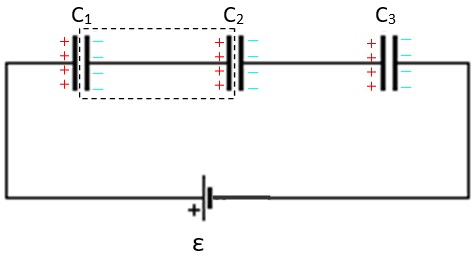
La placa positiva en C1 induce carga negativa en la otra placa de este capacitor, y como ninguna carga neta se puede acumular entre la placa derecha de C1 y la placa izquierda de C2 (recuadro punteado), resulta que esta última se torna positiva.
Nuevamente esta carga positiva induce carga negativa en la placa derecha de C2 y el proceso se repite en el condensador C3, cuya placa derecha se conecta al polo negativo de la batería.
De esta manera, todas las placas quedan con carga “q” de igual magnitud y signos alternados, como aparece en la figura, y en general, cada capacitor queda a distinta diferencia de potencial:
q1 = q2 = q3
ΔV1 ≠ ΔV2 ≠ ΔV3
Pero como la energía se conserva, la suma de cada una de las diferencias de potencial en los capacitores debe ser igual al voltaje en la batería:
1) ΔV1 + ΔV2 + ΔV3 = ε
Ahora bien, se sabe que la capacidad de un condensador se define mediante:
2) \(C=\frac{q}{\Delta V}\)
Donde q es la carga almacenada y ΔV la diferencia de potencial entre sus placas. Sustituyendo 2) en 1) resulta:
3)\(\varepsilon =\frac{q}{{{C}_{1}}}+\frac{q}{{{C}_{2}}}+\frac{q}{{{C}_{3}}}\)
Ya que la carga para los tres condensadores es la misma, puede quedar como factor común:
\(\varepsilon =q\left( \frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}} \right)\)
Por lo tanto la capacitancia equivalente para los tres condensadores en serie Ceq se define a través de:
4) \(\varepsilon =\frac{q}{{{C}_{eq}}}\)
Donde:
5) \(\frac{1}{{{C}_{eq}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}}\)
Si se quiere sustituir la combinación por un solo capacitor, este debe ser de valor igual a Ceq. Cuando se tienen n condensadores en serie, la capacidad equivalente viene dada por la suma:
6) \(\frac{1}{{{C}_{eq}}}=\sum\limits_{i=1}^{n}{\frac{1}{{{C}_{i}}}}\)
Características de capacitores en paralelo
Los capacitores en paralelo están a la misma diferencia de potencial, pero en general pueden tener distintas cargas:
q1 ≠ q2 ≠ q3
ΔV1 = ΔV2 = ΔV3 = ε
Un capacitor equivalente almacena la carga total de la configuración y está a la misma diferencia de potencial que los capacitores participantes, por lo tanto, mediante la ecuación 2):
\(q={{C}_{eq}}\cdot \varepsilon \)
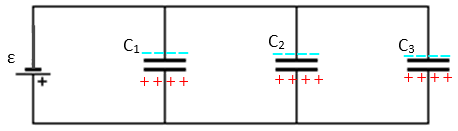
La carga de la configuración es la suma de las cargas en cada capacitor, dado que la carga se conserva:
\(q={{q}_{1}}+{{q}_{2}}+{{q}_{3}}\)
\(q={{C}_{1}}\Delta {{V}_{1}}+{{C}_{2}}\Delta {{V}_{2}}+{{C}_{3}}\Delta {{V}_{3}}\)
Pero ε = ΔV1= ΔV2= ΔV3
\(q=\left( {{C}_{1}}+{{C}_{2}}+{{C}_{3}} \right)\cdot \varepsilon \)
Concluyéndose que:
7)\({{C}_{eq}}={{C}_{1}}+{{C}_{2}}+{{C}_{3}}\)
Por lo tanto, si se quiere sustituir estos tres condensadores por uno solo, la capacidad equivalente de este se obtiene sumando las capacidades C1, C2 y C3. Este resultado se generaliza para n condensadores en paralelo mediante la ecuación:
8) \({{C}_{eq}}=\sum\limits_{i=1}^{n}{{}}{{C}_{i}}\)
Obsérvese que la capacitancia equivalente de una combinación de capacitores en paralelo es mayor que la capacitancia de cada participante, pues hay que sumarlas todas para obtener Ceq. En cambio, la capacitancia equivalente de la combinación en serie, es menor que la más pequeña de las capacidades participantes.
Ejercicio práctico
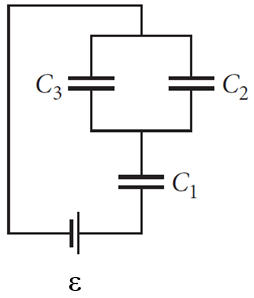
Se tienen tres capacitores cuyas capacitancias se dan más abajo, conectados a una batería de ε =14. 9 V según la configuración mostrada en la figura.
Hallar la diferencia de potencial en el capacitor C2 y en el capacitor C1.
C1 = 3.1 nF
C2 = 1.3 nF
C3 = 3.7 nF
Respuesta
Nótese que los capacitores C2 y C3 están en paralelo, de esta manera, la diferencia de potencial en ambos es la misma, y a su vez el paralelo formado por C2 y C3 se encuentra en serie con C1. Por lo tanto primero hay que determinar la capacidad equivalente del paralelo, a la cual se denotará mediante C23.
De acuerdo a la ecuación 8), el valor de C23 es:
\({{C}_{23}}={{C}_{2}}+{{C}_{3}}=1.3+3.7nF=5nF\)
El circuito queda reducido ahora a:
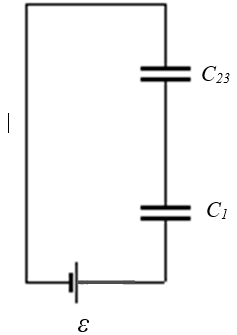
Los capacitores C1 y C23 han quedado en serie, por lo tanto:
ε = ΔV1 + ΔV23
Que a través de la ecuación 4) se transforma en:
\(\varepsilon =\frac{{{q}_{1}}}{{{C}_{1}}}+\frac{{{q}_{23}}}{{{C}_{23}}}\)
La carga en los capacitores conectados en serie es la misma, como se vió anteriormente, entonces:
q1 = q23
Para encontrar los valores de las cargas, se determina la capacidad equivalente de la serie C123 a través de la ecuación 6):
\(\frac{1}{{{C}_{123}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{23}}}=\frac{{{C}_{1}}+{{C}_{23}}}{{{C}_{1}}\cdot {{C}_{23}}}\)
\({{C}_{123}}=\frac{{{C}_{1}}\cdot {{C}_{23}}}{{{C}_{1}}+{{C}_{23}}}=\frac{3.1\times 5}{3.1+5}nF=1.9136nF\)
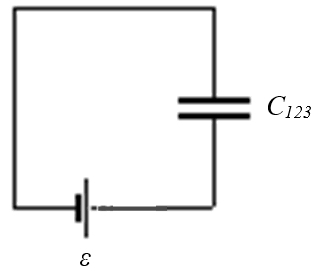
La carga q123 en la asociación de capacitores C123 es, de acuerdo a 4):
\({{q}_{123}}={{C}_{123}}\cdot \varepsilon =1.9136\times {{10}^{-9}}F\times 14.9V=2.8513\times {{10}^{-8}}C\)
Puesto que los capacitores C1 y C23 están en serie, todos poseen igual carga:
\({{q}_{123}}={{q}_{1}}=q{}_{23}\)
De allí que:
\(\Delta {{V}_{23}}=\frac{{{q}_{23}}}{{{C}_{{}^{23}}}}=\frac{2.8513\times {{10}^{-8}}C}{5\times {{10}^{-9}}F}=5.7V\)
Y en el capacitor C1, la diferencia de potencial es:
\(\Delta {{V}_{1}}=\frac{{{q}_{1}}}{{{C}_{{}^{1}}}}=\frac{2.8513\times {{10}^{-8}}C}{3.1\times {{10}^{-9}}F}=9.2V\)
Nótese que ΔV1 + ΔV23 = 14.9 V, ya que la energía se conserva.

Trabajo publicado en: Abr., 2021.