Significado de clustering Definición, ejemplos, y algoritmos (k medias y jerárquico)

Doctor en Ingeniería
Definición formal
Clustering es el proceso de «descubrir» cómo se agrupan los datos. «Descubrir» entre comillas, sí, porque tales agrupamientos (o clusters) no son una propiedad intrínseca de los datos, sino más bien una construcción que hacemos en función de los objetivos con que analizamos los datos.
En el campo de Machine Learning (o aprendizaje maquinal) es frecuente la necesidad de descubrir patrones en los datos. Dependiendo del contexto, suele ocurrir que los elementos de nuestro conjunto de datos pueden agruparse naturalmente en función de ciertas características.
Este tipo de análisis, en que no conocemos de antemano las características de los grupos en que clasificaremos los datos, constituye un ejemplo de aprendizaje no-supervisado (unsupervised learning).
Ejemplos de funcionalidad del Clustering
Pensemos en la última vez que fuimos al supermercado. Inevitablemente los tomates están cerca de la lechuga y el aceite de girasol junto al aceite de oliva, y aunque nunca nos hayamos preguntado por qué, es claro que esto es deliberado.
Nunca hemos visto los tomates entre la harina y la sal, y ni hablar de los tomates desperdigados de a uno en las góndolas del local. Los tomates están todos juntos, y al lado de los tomates están las otras verduras y frutas, formando un cluster que facilita al cliente encontrar lo que busca.

Por supuesto, hay otros contextos (más arraigados al Machine Learning) en los que el clustering es utilizado, como por ejemplo en los sistemas de recomendación. Si a partir de un algoritmo de clustering, Spotify se da cuenta de que la mayoría de la gente que escucha Led Zeppelin escucha también Def Leppard y visceversa, y si nosotros escuchamos Led Zeppelin también, el sistema nos recomendará Def Leppard, dado que Led Zeppelin y Def Leppard están en el mismo Cluster.
Algoritmos: K Medias, y Clustering Jerárquico
Entendiendo las bases del Clustering, resta ver cómo se puede llevar a cabo. Para ello existen varios algoritmos, cuya elección depende del contexto. Es decir, de los datos y de lo que busquemos extraer de ellos. Existen varios algoritmos de Clustering, con variantes cada uno, pero en lo subsiguiente detallaremos dos de los más comúnmente utilizados para ilustrar de qué estamos hablando realmente.
K Medias
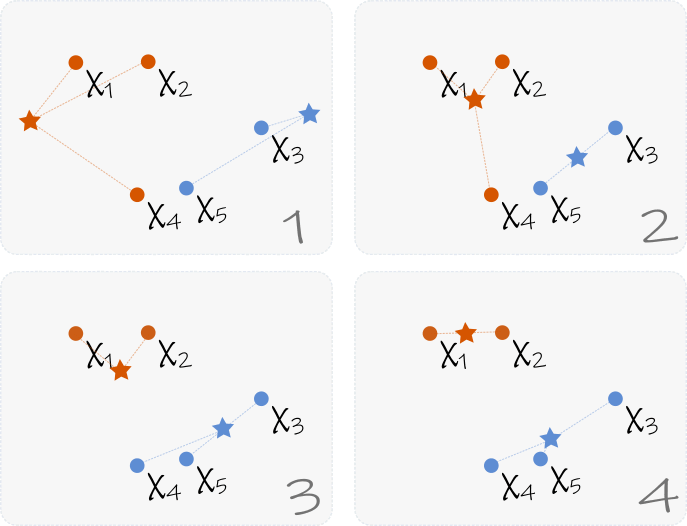
Supongamos que contamos con N observaciones (elementos en nuestro conjunto de datos), y queremos dividir estos datos en K grupos (o Clusters). Para formalizar un poco la notación, digmaos que nuestras observaciones son de la forma \(x_n \in\mathbb{R}^M, \; n = 1, \ldots N\) . El proceso a seguir es el siguiente:
1. Inicializar de manera aleatoria las K medias \(\{y_k\}\).
2. Calcular la distancia \(\|y_k-x_n\|\), para cada n y k.
3. Asignar cada elemento \(x_n\) al Cluster \(C_k\) correspondiente al punto \(y_k\) más cercano.
4. Recalcular cada media como el valor medio de los puntos correspondientes a su Cluster. Es decir \(y_k = \frac{1}{\#C_k}\sum_{x_n\in C_k} x_n\).
5. Repetir el proceso desde el paso 2 hasta que el cambio en las medias \(y_k\) resulte insignificante.
Clustering Jerárquico
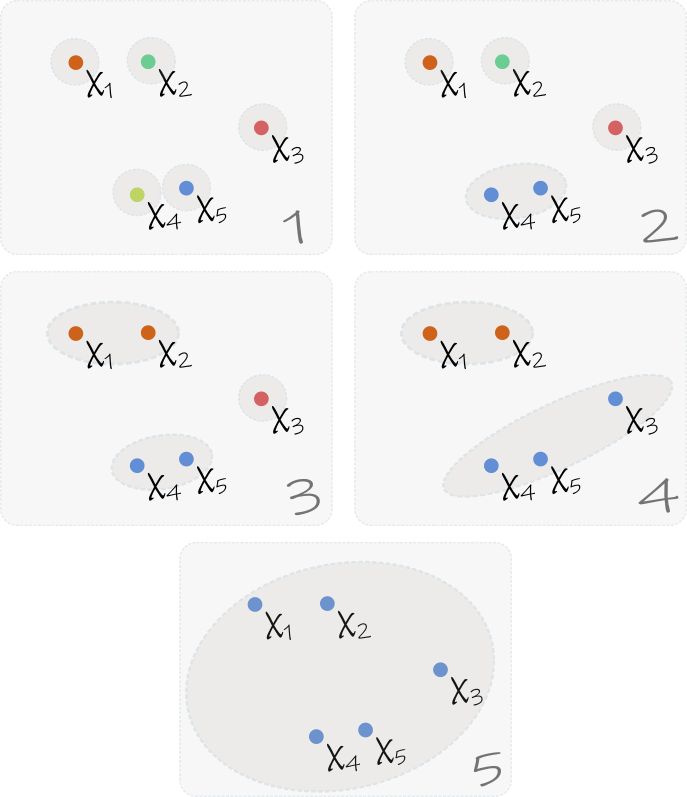
Supongamos que de nuevo contamos con N observaciones de la forma \(x_n \in\mathbb{R}^M, \; n = 1, \ldots N\) . El algoritmo es entonces el siguiente:
1. A cada elemento \(x_n\) le asignamos su propio Cluster \(C_n\).
2. Calculamos la distancia entre cada par de Clusters.
3. Unimos los dos Clusters más cercanos en uno solo.
4. Calculamos la distancia entre el nuevo Cluster y los Clusters previos.
5. Repetimos desde el paso 3 hasta obtener un único Cluster.
Utilizando este algoritmo obtenemos una estructura de Clusters, en lugar de un grupo. Si conocemos el número de Clusters de antemano, podemos detener el algoritmo llegado ese punto, pero cabe destacar que tener una estructura con «Clusters de Clusters» puede ser útil, como en el ejemplo del supermercado donde se organizan el Cluster «Tomates» y el Cluster «Cebollas» dentro del Cluster «Verdulería».
Para facilitar la interpretación de los algoritmos, hemos supuesto que nuestros datos pueden representarse como puntos en \(\mathbb{R}^M\) . Sin embargo, cabe destacar que existen otras maneras de representar los elementos de nuestra base de datos y otras formas de establecer una noción de distancia entre ellos. Asimismo, existen variantes de lo algoritmos aquí propuestos y técnicas de preprocesamiento de los datos que pueden mejorar el desempeño, pero eso ya es tema para un artículo aparte.

Trabajo publicado en: Ene., 2021.