Definición de Cohete

Ángel Zamora Ramírez
Licenciado en Física

Un cohete es un vehículo que se impulsa gracias a la expulsión de gases combustibles a gran velocidad desde su parte posterior. El movimiento de los cohetes es un claro ejemplo de la Tercera Ley de Newton en acción.

Los cohetes han sido una parte fundamental de las misiones espaciales y serán una parte fundamental de futuros viajes tripulados a otros cuerpos del Sistema Solar. Sin embargo, los cohetes también se han sido utilizados para el entretenimiento e incluso con motivos bélicos. A pesar de los distintos fines con los que se usan los cohetes, su principio de funcionamiento es el mismo: Una propulsión a chorro por medio de gases combustibles.

La ecuación del cohete

La manera en la que un cohete se propulsa expulsando gases a gran velocidad es resultado de la Tercera Ley de Newton y de la Conservación del Momento Lineal. En esta sección abordaremos un caso simple de la propulsión de un cohete y aplicaremos todos estos principios para obtener una ecuación general que nos describe el movimiento de un cohete.

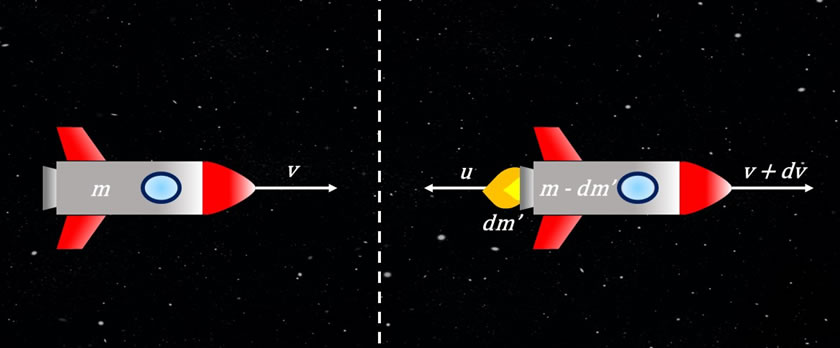
Consideremos a un cohete de masa m que se encuentra en el vacío y que se desplaza en línea recta con una velocidad v con respecto a un marco de referencia inercial. Este cohete enciende su motor y expulsa gas desde su parte posterior con una velocidad u, la masa del gas expulsado es \(dm\prime\). Esto hace que el cohete gane una velocidad dv, por lo que después de su propulsión se mueve a una velocidad \(v+dv\). El gas expulsado era parte de la masa inicial del cohete, por lo que en este instante el cohete tendrá una masa total de m-dm\prime. Esto se puede apreciar en la figura anterior.

Aplicaremos la conservación del momento lineal para obtener una ecuación de movimiento para el cohete. Sean \(p_i\) y \(p_f\) el momento lineal inicial y final, respectivamente, por conservación se tiene:

\(p_i=p_f\)

El momento lineal inicial será simplemente:

\(p_i=mv\)

El momento lineal final será el momento lineal del cohete más el momento lineal del gas expulsado, es decir:

\(p_f=\left(m-dm^\prime\right)\left(v+dv\right)+dm´(v-u)\)

Nótese que la velocidad del gas para este momento lineal es la velocidad relativa del gas con respecto al marco de referencia inercial. Por conservación tenemos entonces que:

\(mv=\left(m-dm^\prime\right)\left(v+dv\right)+dm´(v-u)\)

Desarrollando los términos de la derecha se tiene:

\(mv=mv+mdv-dm^\prime v-dm^\prime dv+dm^\prime v-dm\prime\ u\)

Las cantidades dv y dm\prime son cantidades diferenciales, es decir, muy pequeñas, por lo tanto, vamos a suponer que \(dm^\prime dv\approx0\) para deshacernos de ese término. Tomando en cuenta esto y deshaciéndonos de los términos repetidos obtenemos:

\(mdv=udm\prime\)

En este caso hemos considerado la masa diferencial \(dm\prime\) del gas que es expulsado, no obstante, esta masa la podemos considerar como la masa diferencial que pierde el cohete, es decir que dm^\prime=-dm. Por lo tanto, la ecuación anterior la podemos reescribir como:

\(dv=-u\frac{dm}{m}\)

Integramos esta ecuación desde una velocidad inicial v_0 hasta una velocidad final v, y desde una masa inicial \(m_0\) hasta una masa final m. Es decir que:

\(\int_{v_0}^{v}dv=-u\int_{m_0}^{m}\frac{dm}{m}\)

Al resolver las integrales, evaluarlas en los límites e incorporando el signo negativo al logaritmo obtenido en la parte derecha de la ecuación obtenemos finalmente:

\(v=v_0+u\ln{\left(\frac{m_0}{m}\right)}\)

Esta última es la ecuación que describe de manera general el funcionamiento de los cohetes. Sabemos que \(m_0>m\), por lo tanto, el valor del logaritmo será mayor entre más grande sea la diferencia entre ambas masas. Esto en conjunto con un aumento de la velocidad de propulsión u hace que se maximice la velocidad a la que viaja el cohete. Además, esta es la razón por la que se utilizan cohete con múltiples etapas, el estar propulsando y deshaciéndose de masa del cohete hace que este alcance velocidades más altas.

Ascenso vertical

Otro caso curioso para analizar es considerar un cohete que despega de manera vertical bajo la influencia de la gravedad de la Tierra. Vamos a suponer que el movimiento del cohete es puramente vertical, que la aceleración de gravedad es constante con la altura, que el combustible se quema a una tasa constante y vamos a ignorar los efectos de la resistencia del aire. Esta situación está representada en la siguiente figura:

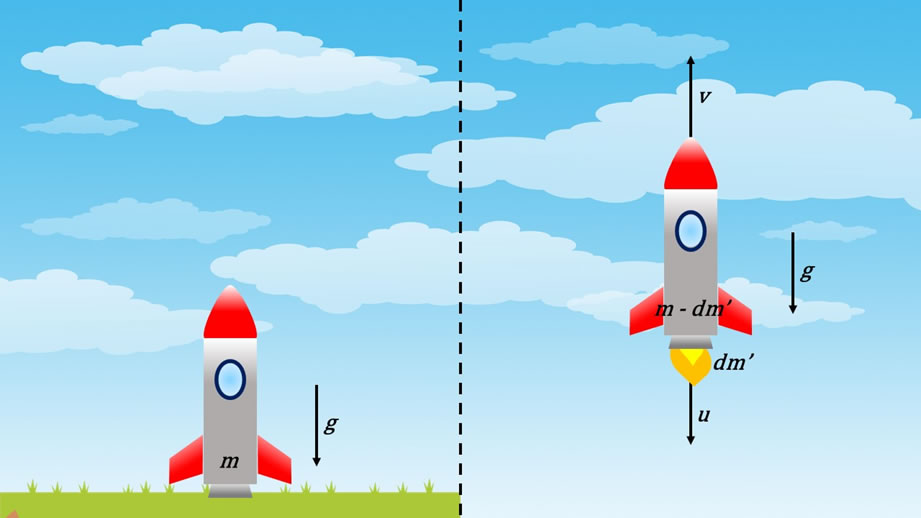
Vamos a tener los mismos parámetros que tenemos en el caso anterior sólo que ahora incluiremos la influencia de la aceleración de gravedad g. La única fuerza que se está ejerciendo sobre el cohete es la fuerza de gravedad, por lo tanto, la fuerza F será:

\(F=-mg\)

Sabemos por Segunda Ley de Newton que:

\(F=\frac{dp}{dt}\)

O bien:

\(Fdt=dp\)

La parte derecha de la ecuación es básicamente la diferencia entre los momentos lineales inicial y final, cosa que calculamos en el caso anterior, particularmente podemos decir que:

\(dp=mdv+udm\)

Juntando todo lo mencionado hasta el momento tenemos que:

\(\left(-mg\right)dt=mdv+udm\)

O equivalentemente:

\(-mg=m\frac{dv}{dt}+u\frac{dm}{dt}\)

Una de las suposiciones que hicimos fue que la tasa a la que se quema el combustible es constante, esa tasa es precisamente el término \(dm/dt\), por lo tanto, podemos decir que:

\(\frac{dm}{dt}=-\alpha\ ;\ \ \ \ \ \alpha>0\)

Donde \alpha es una constante. Esto nos va a ser de utilidad más adelante. Despejando para dv la ecuación que obtuvimos anteriormente obtenemos:

\(dv=-gdt-\frac{u}{m}dm\)

Como podemos darnos cuenta, tenemos tres variables. Es conveniente expresar el lado derecho de la ecuación en términos de una sola variable para poder integrar. Factorizamos el término dm para obtener:

\(dv=\left(-g\frac{dt}{dm}-\frac{u}{m}\right)dm\)

Anteriormente mencionamos que \(\frac{dm}{dt}=-\alpha\), o equivalentemente, \(\frac{dt}{dm}=-\frac{1}{\alpha}\), incorporando esto en la ecuación anterior obtenemos:

\(dv=\left(\frac{g}{\alpha}-\frac{u}{m}\right)dm\)

Y ahora sí podemos integrar esta última expresión. Vamos a suponer que el cohete parte del reposo sobre la superficie de la Tierra. Integraremos entonces la ecuación anterior desde \(v=0\) hasta una velocidad final \(v\), y desde una masa inicial \(m_0\) hasta una masa final m. Tenemos entonces:

\(\int_{0}^{v}dv=\int_{m_0}^{m}\left(\frac{g}{\alpha}-\frac{u}{m}\right)dm\)

Separando la suma de integrales del lado derecho tenemos:

\(\int_{0}^{v}dv=\int_{m_0}^{m}{\frac{g}{\alpha}dm}-u\int_{m_0}^{m}\frac{dm}{m}\)

Integrando y evaluando en los límites de integración se tiene

\(v=\frac{g}{\alpha}\left(m-m_0\right)-u\ln{\left(\frac{m}{m_0}\right)}\)

Como \(\frac{dm}{dt}=-\alpha\), entonces, \(\frac{\Delta m}{\alpha}=-\Delta t\). Si el tiempo inicial lo fijamos en \(t=0\) y el tiempo final es simplemente \(t\), podemos decir que \(\frac{\left(m-m_0\right)}{\alpha}=t\). Tomando en cuenta esto en la ecuación anterior e incorporando el signo negativo dentro del logaritmo obtenemos finalmente que:

\(v=u\ln{\left(\frac{m_0}{m}\right)}-gt\)

Esta es la ecuación que describe el movimiento vertical de un cohete que despega desde la superficie terrestre.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Feb., 2024.

Datos para citar en modelo APA: Zamora Ramírez, A. (febrero, 2024). Definición de Cohete. Significado.com. Desde https://significado.com/cohete/