Significado de distancia y desplazamiento Definición, diferencia, propiedades, y dimensiones

Licenciada en Física
Definición formal
Ambas magnitudes, distancia y desplazamiento, participan en la descripción del movimiento de un cuerpo, pero no son sinónimos. La distancia entre dos puntos A y B es la longitud medida entre ellos, independientemente de si se mide desde A hasta B o desde B hasta A. En cambio, el desplazamiento es la diferencia entre la posición final e inicial, involucrando aspectos geométricos de dirección y sentido.
Se puede tener un desplazamiento nulo, pese a haber recorrido una gran distancia. Para esto solo basta que el punto de partida sea el mismo que el de llegada, es decir, recorrer un camino cerrado.
Matemáticamente hablando, la distancia es un escalar, del que solo bastan un número y una unidad adecuada para especificarlo. Y en cambio, el desplazamiento es un vector, que además de la parte numérica, tiene dirección y sentido. Cualquier cálculo que se haga con el desplazamiento lleva implícitos estos tres aspectos.
Ambas magnitudes se miden en unidades de longitud, como metros, centímetros, pies, pulgadas y más. En el Sistema Internacional de Unidades SI, la unidad apropiada para la distancia y el desplazamiento es el metro, abreviado m. Los siguientes ejemplos aclaran las similitudes y las diferencias entre los dos conceptos.
Diferencia entre distancia y desplazamiento en una dimensión
El movimiento más sencillo ocurre sobre una línea recta, con una coordenada espacial única para describirlo. A esta recta se le da un nombre, por ejemplo, el eje “x”, y sobre ella se marca un punto de referencia para el movimiento, que es el origen O:

Tómese un móvil que partió de x = 0m y recorrió 3m hacia la derecha. La distancia recorrida es precisamente 3m y el desplazamiento fue de 3m hacia la derecha. La distancia se puede denotar con la letra “d”, y el desplazamiento como Δx. El signo + indica movimiento hacia la derecha, y el signo – hacia la izquierda.

Entonces:
d = 3m
Δx = + 3m
El signo + puede omitirse, sobreentendiendo que, si no aparece, la cantidad es positiva.
Ahora bien, si el móvil partió de x = 0m y recorrió 3m hacia la izquierda, la distancia fue igualmente 3m, pero el desplazamiento fue negativo, porque el móvil viajó en sentido contrario. Por lo tanto:
d = 3m
Δx = − 3m

Ahora que el móvil se encuentra en la posición x = −3, quiere viajar hasta x = +5m. En este caso: ¿cuáles son la distancia recorrida y el desplazamiento?

Pues bien, para ir desde x =−3m hasta x = +5m hay que recorrer un total de 8 m, por lo tanto:
d = 8m
Y el desplazamiento es la variación en la posición Δx, que es simplemente la diferencia entre la posición final y la posición inicial:
Δx = +5m – (−3m) = +5m + 3m = +8m
Propiedades del desplazamiento
Nótese que la distancia siempre es una cantidad positiva, pero que el desplazamiento, aunque de igual magnitud, puede ser negativo o positivo. La diferencia es que el desplazamiento indica hacia dónde se produjo el movimiento, y esta es una información muy importante a la hora de ofrecer una descripción concisa.
También es importante destacar que el móvil puede estar viajando sobre el eje negativo, pero su desplazamiento ser positivo. No hay problema alguno, pues el desplazamiento simplemente apunta en un sentido específico: el del movimiento.
Finalmente, en una dimensión se puede establecer que:
Desplazamiento = posición final – posición inicial
Δx=xfinal-xinicial
De manera que si el móvil parte de un punto determinado, va y viene varias veces, y finaliza el recorrido en el mismo punto, su desplazamiento fue nulo. ¡Pero la distancia recorrida no!
Distancia y desplazamiento en dos dimensiones
En dos dimensiones se requieren dos coordenadas para especificar una cierta posición. En el ejemplo siguiente, el móvil se encuentra inicialmente en el punto A, de coordenadas (2m, 6m) y después se mueve hasta B (7m, 3m).
El móvil puede utilizar diversas trayectorias para ir desde A hasta B. En la figura se muestran los caminos C1 y C2, de entre muchos posibles. Cuantas más vueltas se den entre los dos puntos, más larga es la distancia, pero el desplazamiento seguiría siendo el mismo: desde A hasta B.
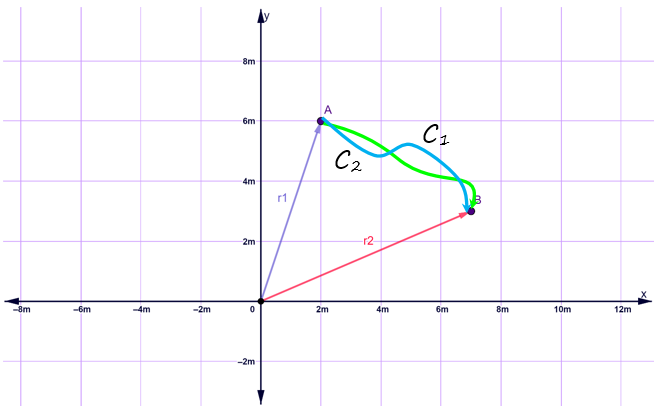
Cuando se trabaja en dos dimensiones, hay que especificar tanto la coordenada “x” como la “y”.
Como siempre, la posición es un vector que va desde el origen del sistema de coordenadas, el punto (0m,0m) hasta el lugar donde está el móvil en un determinado instante. Se denota con la letra r, en negrita, o bien con una flechita encima: r ⃗.
El desplazamiento se denota Δr ⃗ y viene dado por:
Δr ⃗=r ⃗2-r ⃗1
Los vectores de posición r ⃗1 y r ⃗2 del ejemplo son, respectivamente:
r ⃗1=〈2m,6m〉
r ⃗2=〈7m,3m〉
Nótese que se utilizaron corchetes (“brackets”), en vez de paréntesis, para enfatizar el carácter vectorial y establecer la diferencia con los puntos en el plano.
El desplazamiento se calcula restando componente a componente:
Δr ⃗=r ⃗2-r ⃗1=〈7m,3m〉-〈2m,6m〉=〈(7m-2m);(3m-6m〉=〈5m,-3m〉
El vector desplazamiento resultante es:
Δr ⃗ = 〈5m,-3m〉
En forma gráfica:
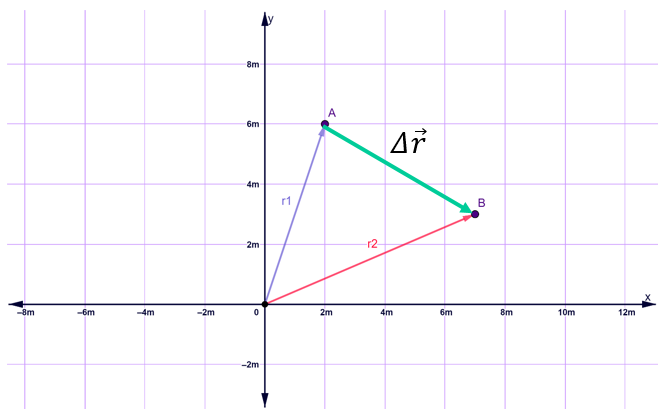
La magnitud del desplazamiento es simplemente la distancia medida entre los puntos A y B:
\(\left| \text{ }\!\!\Delta\!\!\text{ }\vec{r} \right|=\sqrt{{{\left( 5m \right)}^{2}}+{{\left( -3m \right)}^{2}}}=5.83m\)
¿Fue esta la distancia recorrida? Si el móvil hubiese ido en línea recta desde A hasta B, sí.
Pero el móvil pudo haber ido por distintos caminos y la distancia sería diferente.
Un ejemplo se muestra a continuación: partiendo de A, el móvil recorre 4m hacia, luego 5 m a la derecha y finalmente 1m hacia arriba, para llegar a B.
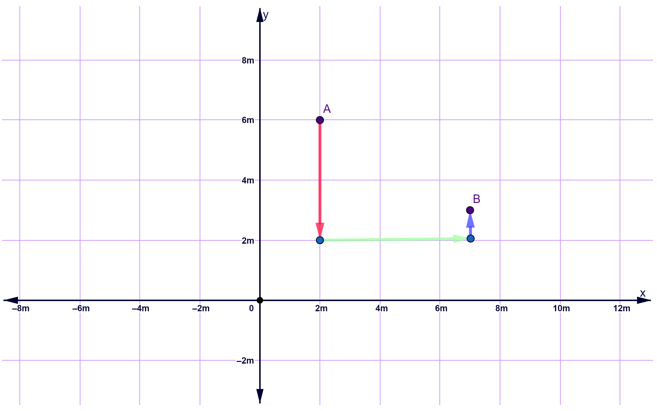
En tal caso la distancia recorrida es:
d = 4m + 5m + 1m = 10m

Trabajo publicado en: Jul., 2021.