Significado de trabajo (en física) Definición, características, y fórmulas

Licenciada en Física
Definición formal
El trabajo, a instancias de la física, es una magnitud escalar que se asocia a la capacidad de la fuerza capaz de afectar la posición de un objeto, o incluso de oponerse a él. No es exactamente el significado que se le asocia a la palabra -trabajo- en el lenguaje ordinario, sino algo más conciso: transferir energía al móvil o lograr que éste ceda la suya a otro sistema.
Como toda magnitud física, el trabajo tiene una expresión matemática, así que llamando W al trabajo, F a la fuerza y d al desplazamiento (estos últimos en negrita ya que son vectores y de esta manera se distinguen de los escalares), definiéndose como: W = F•d
El punto simboliza el producto escalar entre los vectores F y d, una de las tres clases de producto que se hacen entre vectores, y cuyo resultado es un escalar. Al producto escalar entre dos vectores también se le llama “producto punto”, por razones obvias: para denotarlo se hace uso de un punto bien marcado.
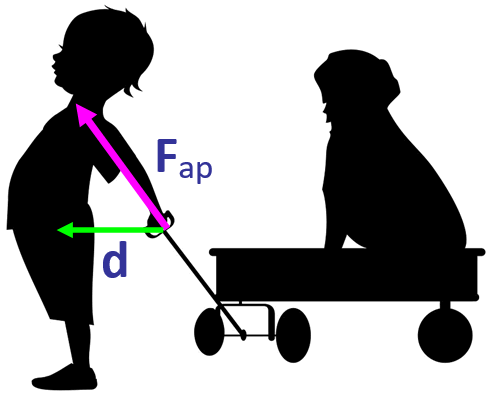
Calcular el producto punto entre dos vectores es muy sencillo: se multiplican las magnitudes de cada uno por el coseno del ángulo que ambos forman entre sí. Si entre F y d hay un ángulo θ, pues el producto escalar entre ellos es: W = Fdcosθ
Unidades del trabajo
Las dimensiones del trabajo corresponden al producto Fuerza × desplazamiento y en el Sistema Internacional de Unidades SI la unidad es:
Newton × metro = N×m = 1 Joule = 1 J
El joule es la unidad SI para el trabajo, nombrada así en honor al científico James Prescott Joule (1818-1889).
El ergio, la unidad del sistema cgs, también aparece en la literatura aunque con menos frecuencia. Se define como el producto entre la dina y el centímetro:
1 dina×cm = 1 ergio.
Y en el sistema anglosajón se usa:
1 libra-fuerza × pie.
Además hay otras unidades que tradicionalmente se utilizan en ciertas áreas específicas, como la caloría, el BTU (British Thermal Unit) y el kilovatio-hora.
Características del ángulo entre la fuerza y el desplazamiento
En la definición W = Fdcosθ se pone de manifiesto un aspecto muy importante del trabajo: el ángulo entre la fuerza y el desplazamiento determina que el trabajo sea:
. Máximo
. Cero
. Mínimo
Estos casos se ilustran en la siguiente figura, junto al caso general en el cual la fuerza y el desplazamiento forman un ángulo θ.

Cuando el trabajo es máximo, la fuerza favorece completamente al desplazamiento y aumenta la energía cinética del móvil (energía asociada al movimiento). En cambio, cuando el trabajo es mínimo, la fuerza se opone al desplazamiento y la energía cinética del objeto disminuye, como en el caso del rozamiento cinético, que tiende a frenar los móviles.
Finalmente, la acción de una fuerza perpendicular al movimiento no modifica la energía cinética del móvil, como la fuerza centrípeta, que siempre es perpendicular a la trayectoria.
Nótese que el trabajo hecho por una fuerza puede ser tanto positivo como negativo o nulo, dependiendo del valor de cos θ. Más adelante se verá un ejemplo ilustrativo resuelto que muestra estas situaciones.
El trabajo neto
Puede que sobre un cuerpo actúe más de una fuerza, pero no hay problema, el trabajo neto es la suma algebraica de los trabajos individuales hechos por cada fuerza, e igual al trabajo realizado por la fuerza neta o suma vectorial de todas las fuerzas que actúan sobre el móvil:
\({{W}_{neto}}=\sum\limits_{i}{{{W}_{i}}}\)
Fórmulas: ejercicio de aplicación

Marty jala el trineo de 8 kg donde va sentada Joan, de 50 kg con una cuerda liviana que forma un ángulo de 36.9º con la horizontal. La fuerza aplicada es constante y de magnitud 100 N, y además existe roce cinético entre el trineo y el suelo, siendo el coeficiente de roce igual a 0.1.
Cuando el trineo se ha movido horizontalmente una distancia igual a 25 m, calcular:
a) Los trabajos hechos por cada una de las fuerzas que actúan sobre el trineo.
b) El trabajo neto.
Respuestas
a) Para calcular el trabajo hecho por cada una de las fuerzas, es necesario hacer un diagrama de cuerpo libre que muestre cómo actúan sobre el trineo y su ocupante.
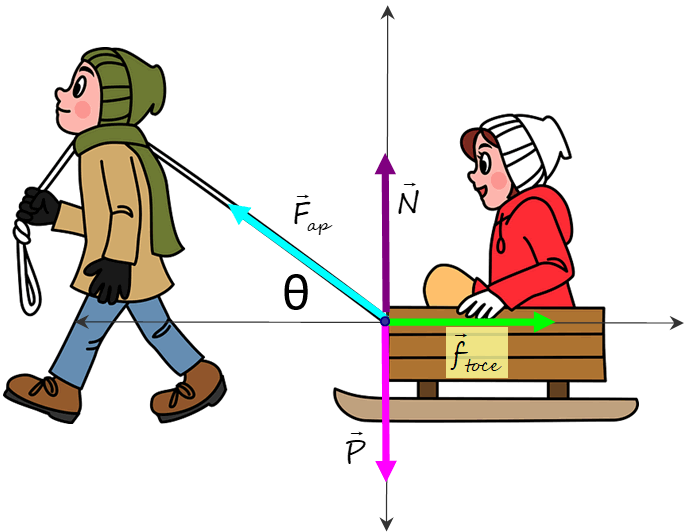
Estas fuerzas son:
.La fuerza aplicada por Marty Fap
.El peso del sistema Joan-trineo P
.El roce con el suelo froce
.La normal que ejerce el suelo sobre el sistema Joan-trineo y que le sirve de apoyo N.
Recuérdese que en texto impreso, las fuerzas se denotan con negrita o con una flecha encima.
Trabajo hecho por la fuerza aplicada
Wap = Fap ×d ×cos θ
Los datos del enunciado son:
.Magnitud de la fuerza aplicada: 100 N
.Magnitud del desplazamiento = distancia recorrida: 25 m
.Ángulo entre la fuerza y el desplazamiento: θ = 36.9º
Sustituyendo:
Wap = 100N ×25m ×cos 36.9º = 1999.2 J
Trabajo hecho por el peso y la normal
Estas fuerzas son perpendiculares al desplazamiento y por lo tanto no hacen trabajo.
Trabajo hecho por el roce cinético se expresa en:
froce = μkN
Donde μk es el coeficiente de roce cinético igual a 0.1. En cuanto a la normal, a partir del diagrama de cuerpo libre y la aplicación de la segunda ley de Newton a las fuerzas verticales:
N + Fap∙senθ – mg = 0
N = mg – Fap∙senθ = (50+8) kg×9.8 m/s2 – 100 N×sen36.9º = 508.4 N
Por lo tanto:
froce = 0.1×508.4 N = 50.84 N
El trabajo hecho por el roce es:
Wroce = 50.84 N×25 m×cos 180º = −1270.9 J
b) El trabajo neto es la suma algebraica de los trabajos hechos por cada una de las fuerzas:
Wneto = 1999.2 J + 0 J + 0 J − 1270.9 J = 728.3 J
Dado que el trabajo neto es positivo, la energía cinética del sistema se incrementó durante el recorrido.

Trabajo publicado en: Dic., 2020.