Significado de fuerza de rozamiento Definición, fricción estática y cinética, y ejercicio

Licenciada en Física
Definición formal
La fuerza de rozamiento es el efecto surgido del contacto entre dos superficies a causa de la interacción entre las moléculas.
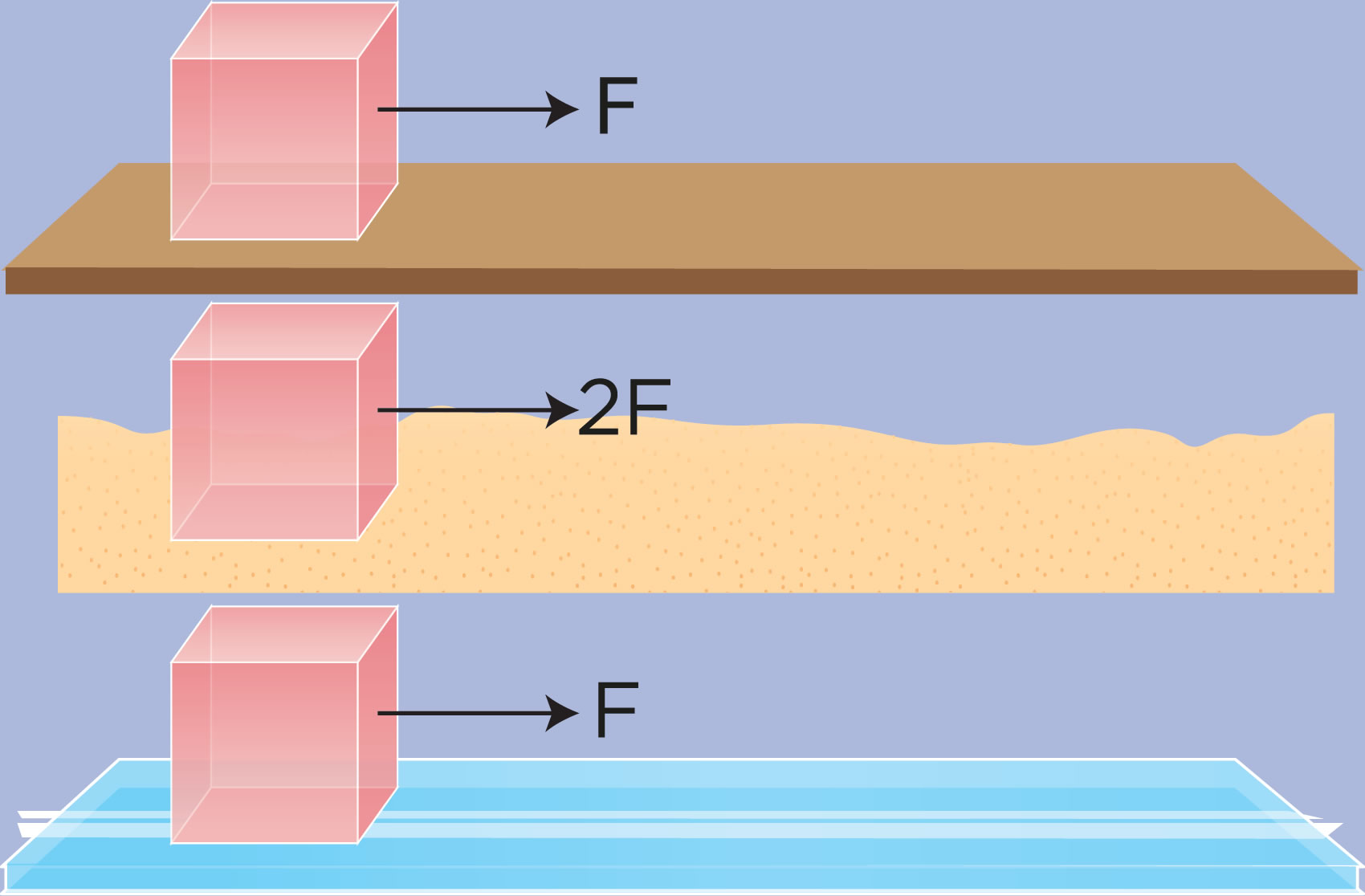
Resulta que, por más lisas y suaves que parezcan las superficies al tacto, cuando se ven a través del microscopio, se distinguen numerosas rugosidades que se enganchan unas con otras. Además, la cercanía entre moléculas hace que ocurran fuerzas de atracción entre ellas, que colaboran al efecto total de la fricción.
Tienen una suerte de ambivalencia: por una parte, se sabe que ocasionan el desgaste en las partes mecánicas, motivo por el cual los ingenieros luchan por evitarlas creando todo tipo de lubricantes para mecanismos. El roce tampoco es bienvenido en el cuerpo humano, ya que con el tiempo, los cartílagos de las articulaciones se desgastan y el rozamiento causa molestias y dolor.
Pero por otra parte, sin rozamientos no sería posible caminar, ni tampoco los automóviles podrían rodar por las carreteras, ya que patinarían todo el tiempo. En muchas autopistas con pendientes pronunciadas se colocan de tanto en tanto rampas de frenado, consistentes en tramos paralelos de pavimento de gravilla irregular, que ayudan a los conductores cuyo sistema de freno está averiado a detener el vehículo.
Cuando se ponen dos objetos en contacto, la fuerza de rozamiento se opone al deslizamiento entre las superficies, por ejemplo, si se tiene un libro sobre una mesa inclinada, hay dos opciones:
i) Mucha fricción hace que el libro no deslice sobre la mesa, manteniéndolo en equilibrio estático.
ii) Pero si la fricción no es suficiente para impedir el movimiento, el libro desliza y la fuerza de rozamiento se opone al deslizamiento y disminuye su velocidad.
En el caso i) la fricción que actúa se llama fricción estática y en el caso ii) se trata de la fricción dinámica o fricción cinética.
Fricción estática
La fuerza de rozamiento estático o fricción estática actúa cuando las superficies están en reposo, una respecto a la otra. Supóngase que se tiene un bloque sobre una superficie horizontal, al cual se le aplica una fuerza pequeña F (las fuerzas son vectores y por eso se denotan con letra negrita o con una flecha encima en texto impreso, para distinguirlas de los escalares):
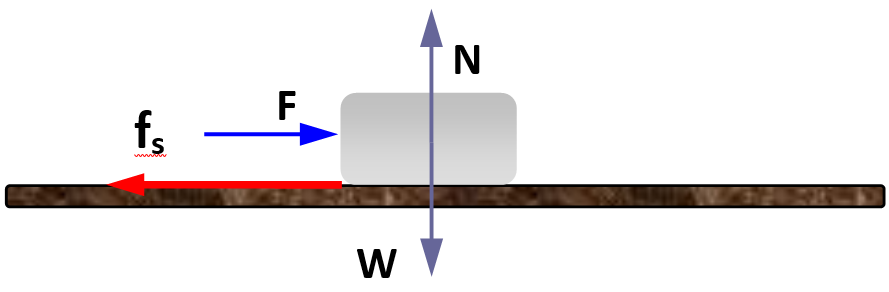
El dibujo muestra el diagrama de cuerpo libre del bloque, en el cual aparecen señaladas todas las fuerzas que actúan sobre él. Se incluyen: la normal N y el peso W, dirigidas verticalmente y que se cancelan entre sí, la fuerza F de pequeña magnitud en azul, aplicada por algún agente externo como la mano de la persona que empuja y finalmente fs, la fuerza de roce estático, en rojo que actúa mientras el bloque no se empiece a moverse.
La magnitud de F se puede incrementar, y a medida que se hace, la fuerza de roce estático también aumenta su magnitud, ya que se ajusta para asegurar el equilibrio del bloque. Claro que si F sigue en aumento, llega un punto en que se iguala su magnitud con la de fs, siendo este su valor máximo. Entonces el bloque está a punto de moverse (movimiento inminente) y una vez que F supere a fs, el bloque efectivamente deslizará sobre la superficie.
El físico francés Charles Auguste Coulomb (1736-1806), el mismo de la ley de Coulomb para cargas eléctricas puntuales, observó en su laboratorio que:
– El roce estático siempre es paralelo a las superficies en contacto.
– Su valor máximo es proporcional al de la fuerza normal, siendo la constante de proporcionalidad el coeficiente de roce estático μs y su valor mínimo es 0.
Por lo tanto:
\(0\le {{f}_{s}}\le {{\mu }_{s}}N\)
Y:
fs (máx) = μs∙N
El coeficiente de roce estático μs es una cantidad adimensional cuyo valor se determina mediante pruebas experimentales, ya que cada par de superficies tiene un coeficiente característico.
Fricción cinética
Ahora, la fuerza F aplicada externamente supera el roce estático y el bloque se mueve sobre la superficie. Una vez que esto sucede entra en acción la fuerza de rozamiento cinético, que se opone al movimiento. Su magnitud también es proporcional a la de la fuerza normal, pero la constante es diferente: es el coeficiente de roce cinético μk.
En la práctica ocurre que μk < μs y por eso resulta más fácil mantener un objeto en movimiento sobre una superficie áspera, que lograr que empiece a moverse. Es importante destacar que ni la fuerza de rozamiento estático ni la de roce cinético dependen del área de contacto entre las superficies.
Ejercicio resuelto
En el problema del bloque de masa m que desliza cuesta abajo por el plano inclinado partiendo del reposo ¿cuál es la aceleración que adquiere el bloque si entre su superficie y la del plano inclinado hay un coeficiente de roce dinámico μk?
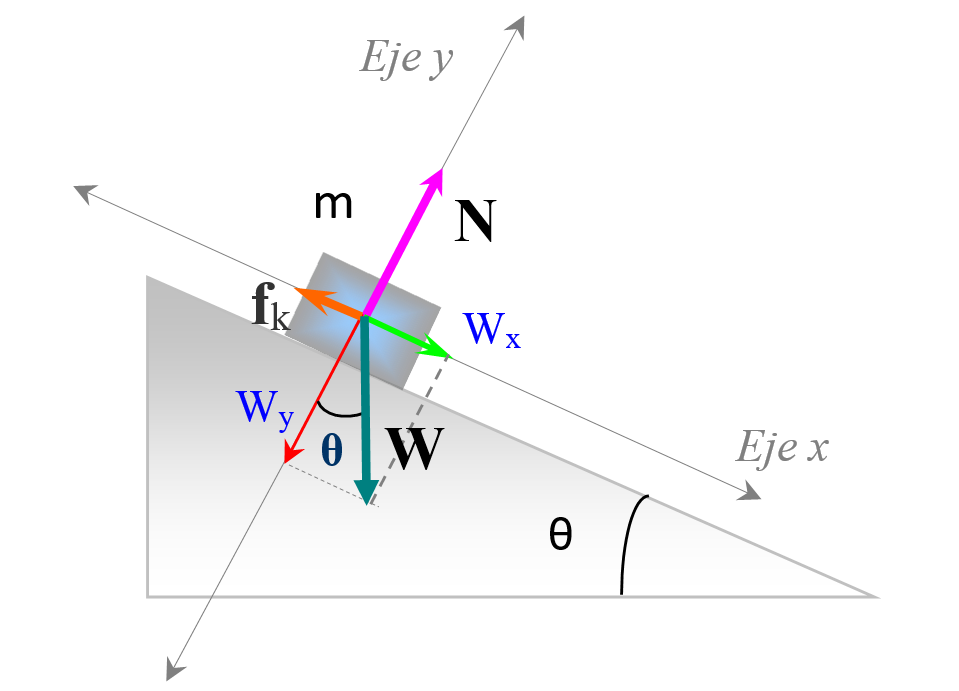
Respuesta
El primer paso es dibujar el diagrama de cuerpo libre mostrando todas las fuerzas que actúan sobre el cuerpo: la normal N, el peso W y el roce dinámico fk, ya que el bloque se encuentra en movimiento. El modelo seguido es el modelo de partícula y se supone que toda la masa del bloque está concentrada en su centro.
Eligiendo el sistema de coordenadas con el eje x paralelo a la superficie del plano y la dirección positiva como la dirección del movimiento, la segunda ley de Newton resulta en las siguientes ecuaciones, una en cada dirección:
∑ Fy = N − Wy = m∙ay = 0
∑ Fx = Wx − fk = m∙ax
La aceleración en la dirección del eje y es nula, por eso la normal y la componente vertical del peso se cancelan mutuamente. En cuanto a las componentes rectangulares del peso son:
Wx = mg∙sen θ
Wy = mg∙cos θ
Donde g es la magnitud de la aceleración de la gravedad. Por su parte, según lo visto anteriormente, la magnitud del rozamiento es:
fk = μk∙N
De la ecuación de fuerzas a lo largo del eje y se tiene:
N − Wy = 0
N = Wy = mg∙cos θ
Por lo tanto:
fk = μk∙ mg∙cos θ
Sustituyendo esto en la ecuación para las fuerzas a lo largo del eje x:
Wx − fk = m∙ax
Wx − μk∙ mg∙cos θ = m∙ax
mg∙sen θ − μk∙ mg∙cos θ = m∙ax
La masa m es factor común en los tres términos y se cancela, quedando:
ax = g∙sen θ − μk∙ g∙cos θ = g (sen θ − μk∙cos θ)
Si no existiera la fuerza de rozamiento, la aceleración del bloque sería ax = g∙sen θ, pero la fricción disminuye la aceleración y con ello la velocidad del bloque durante el descenso.

Trabajo publicado en: Nov., 2020.
Ilustraciones: Koray