Significado de principio de Bernoulli Definición, fórmula y ecuaciones de deducción

Licenciada en Física
Definición formal
El Principio de Bernoulli remite a la comprensión de la manera en la que actúa un fluido en movimiento durante una trayectoria contenida en un tubo de corriente, estableciendo que la energía del fluido se mantiene siempre constante en todo el camino.
Supone una manifestación de la conservación de la energía mecánica, la misma que se aplica a una partícula en movimiento bajo la acción de fuerzas conservativas. Así lo descubrió el científico suizo Daniel Bernoulli (1700-1782), quien lo expusiera en su trabajo Hidrodinámica hacia 1738.
Para extender la conservación de la energía mecánica a los fluidos en movimiento, estos deben cumplir dos condiciones importantes: 1) Carecer de rozamiento interno, es decir, viscosidad y 2) Mantener constante su densidad, lo que es equivalente a decir que son fluidos incompresibles. Los fluidos con estas características se consideran fluidos ideales.
Fórmula del Principio de Bernoulli: La energía de un fluido en movimiento
Muchos fluidos, incluyendo al agua, tienen, bajo determinadas circunstancias, un comportamiento cercano al de los fluidos ideales, y por lo tanto es válido el principio de Bernoulli para hacer los cálculos relativos a su comportamiento. El principio se puede expresar en:
Presión + Energía cinética/unidad de volumen + Energía potencial/unidad de volumen = Constante
De acuerdo a esto, la energía del fluido en movimiento se debe a tres contribuciones importantes:
– El trabajo asociado a las diferencias de presión.
– La energía cinética debida al movimiento del fluido.
– La energía potencial gravitatoria procedente de la elevación sobre el nivel de referencia.
Ecuaciones para la deducción del Principio de Bernoulli
Si ahora se sustituyen las ecuaciones para cada término, es posible conseguir una ecuación matemática apropiada. La energía cinética K de una partícula de masa m y velocidad v, viene dada por la expresión:
\(K = \frac{1}{2} mv^2\)
Mientras que su energía potencial gravitatoria U es:
\(U = m \cdot g \cdot h\)
Donde h es la altura a la que se encuentra la partícula y g es el valor de la aceleración de la gravedad. Como no es fácil seguir la pista a cada una de las innumerables partículas que conforman un fluido, es preferible utilizar la densidad ρ (letra griega que se lee “rho”) en vez de la masa.
La densidad de una sustancia es la razón entre la masa m y el volumen V de una porción:
\(\rho =\frac{m}{V}\)
Escritas en términos de la densidad, la energía cinética y la energía potencial se transforman respectivamente en:
\(K = \frac{1}{2} \rho V v^2\)
\(U = \rho V \cdot g \cdot h\)
Como el principio de Bernoulli establece que la suma de:
– Presión
– Energía cinética por unidad de volumen
– Energía potencial por unidad de volumen
Es una constante, el volumen V simplemente desaparece de las expresiones anteriores y se puede escribir, simplificando:
\(P + \frac{1}{2} \rho \cdot v^2 + \rho \cdot g \cdot h = constante\)
Nótese que cada uno de los términos que componen la ecuación tiene unidades de presión. En el Sistema Internacional de unidades SI, la unidad para la presión es el pascal, abreviado Pa.
La ecuación también permite tomar dos puntos arbitrarios dentro del tubo por el que circula el fluido, por ejemplo los puntos 1 y 2, y establecer para ellos la siguiente relación:
\(P_{1} + \frac{1}{2} \rho \cdot v_{1}^2 + \rho \cdot g \cdot h_{1} = P_{2} + \frac{1}{2} \rho \cdot v_{2}^2 + \rho \cdot g \cdot h_{2} = constante\)
De esta manera, conocidas las condiciones del fluido en una de las secciones, es posible conocer también las condiciones en otra.
Tubería horizontal
La ecuación de Bernoulli se simplifica para una tubería horizontal, pues al comparar dos puntos 1 y 2 de igual altura, \(h_{1} = h_{2}\) y los términos que contienen la altura se cancelan, así la ecuación se reduce a:
\(P_{1} + \frac{1}{2} \rho \cdot v_{1}^2 = P_{2} + \frac{1}{2} \rho \cdot v_{2}^2 = constante\)
Cuando se incrementa la presión en una sección del tubo, es evidente que la velocidad del fluido tiene que disminuir, porque la suma de ambos términos se debe mantener siempre igual. Y si por el contrario la presión disminuye, entonces la velocidad aumenta por la misma razón. Este es un concepto clave en la aplicación del principio.
¿Y qué pasa cuando las tuberías tienen distinto ancho? Todo el mundo conoce el efecto que tiene poner el dedo en la boquilla de la manguera: el agua sale más de prisa.
En efecto, cuando se estrecha el conducto, la velocidad del agua aumenta, pero la presión disminuye en la parte estrecha de la boquilla, aunque al colocar la mano enfrente se siente el impacto del chorro de agua. Esta fuerza nada tiene que ver con la presión con la que sale el agua, sino con la cantidad de movimiento de las partículas de agua que forman el chorro. Lo cierto es que la presión del agua es mayor en la sección alejada de la boquilla.
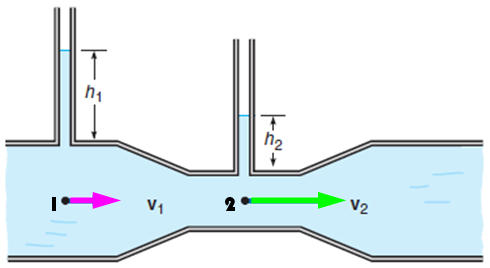
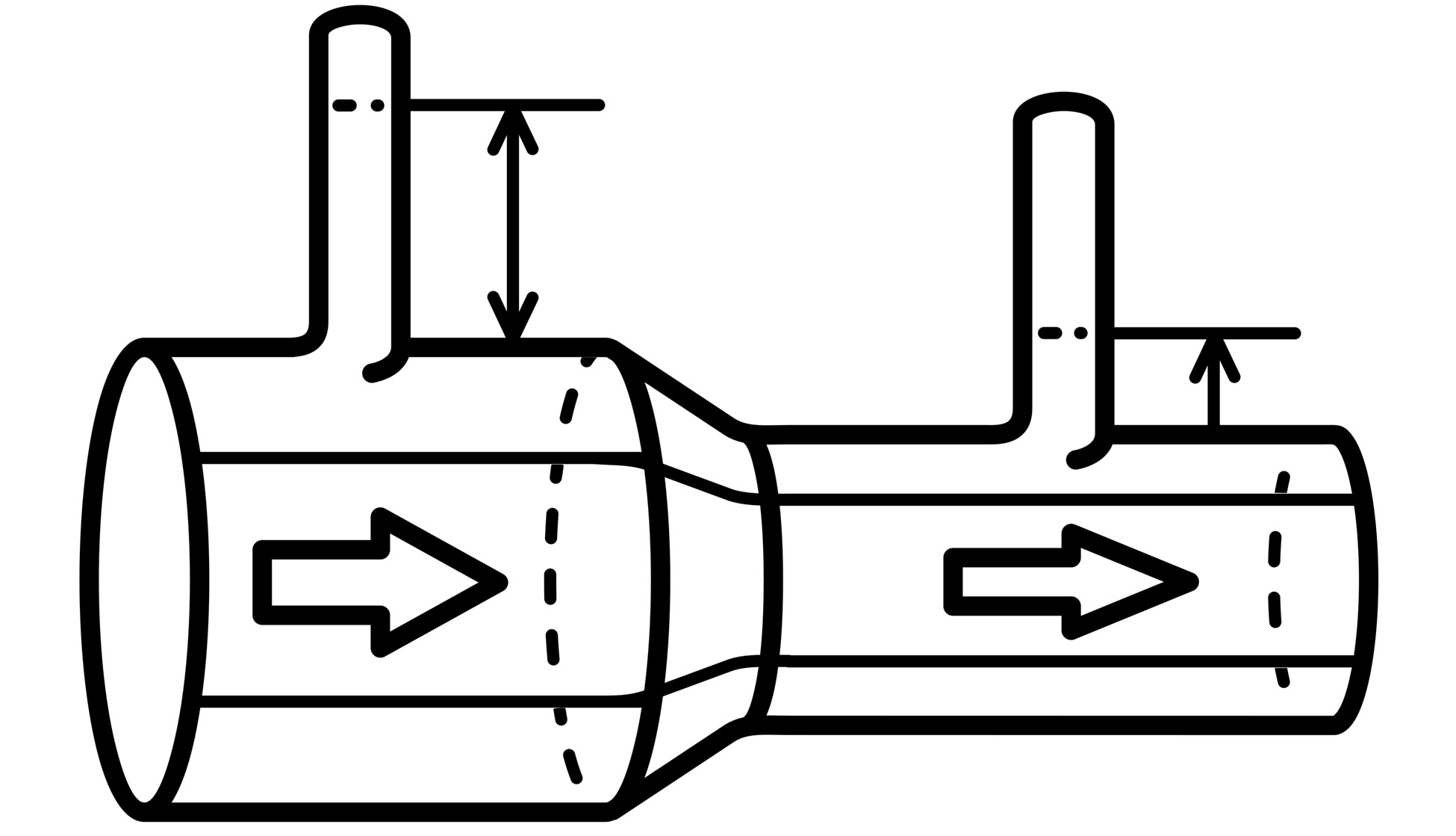
Una forma de medir la presión en un conducto por el que circula un fluido consiste en poner tubitos estrechos, verticales y abiertos en los distintos tramos. La altura a la que sube el agua es proporcional a la presión en la sección: cuanto mayor sea, asimismo es la presión.
En la figura se observa que la presión en la sección 1, que es más ancha, es mayor que la de la sección 2, más estrecha, pues \(h_{1} > h_{2}\). Y en cambio, \(v_{2}\) es mayor que en \(v_{1}\). Esta es una consecuencia de otro principio de conservación: el de la masa. Si no hay pérdidas de fluido en el conducto, el volumen de fluido que transita por unidad de tiempo, llamado caudal, también se mantiene constante. El caudal es el producto de la velocidad por el área de sección transversal, si esta disminuye, la velocidad aumenta para que el producto siga siendo constante.

Trabajo publicado en: Nov., 2020.
Ilustraciones: Olena Panasovska