Significado de probabilidad Definición, explicación, y propiedades

Doctor en Ingeniería
Definición formal
La probabilidad es la responsable por asignar una descripción numérica al grado de certidumbre que tenemos respecto de cierto evento o suceso x.
Típicamente, la probabilidad de que ocurra un evento A, P(A), se denota con un número entre 0 y 1, donde P(A)=0 indica seguridad en la no-ocurrencia del evento y P(A)=1 indica total seguridad en su ocurrencia.
Explicación práctica
Resulta importante tener en cuenta que no existe una manera única o correcta de asignar probabilidades a eventos reales. Si tiramos un dado, por ejemplo, el proceso físico que gobierna la caída del dado es puramente determinístico. Una vez que el dado está en el aire y en movimiento, las leyes de la física determinarán el lugar en que cae y la cara que queda hacia arriba.
Es nuestra imposibilidad de calcular y anticipar el resultado lo que nos hace decir que la probabilidad de que salga 3 en un dado de seis caras es 1/6.

Factores de probabilidad sobre un evento real
Existen, a grandes rasgos, tres maneras de asignar probabilidad a un evento real.
1) Frecuentista: Dado un experimento de carácter aleatorio, decimos que un evento A tiene probabilidad p si la frecuencia relativa con que ocurre ese evento cuando el experimento se repite muchas veces es p. En el caso del dado, si lo tiramos 60 mil veces y obtuvimos 3 unas 10 mil veces, entonces \(P(\text{obtener 3}) = 10000/60000 = 1/6\) .
2) Otra manera de asignar probabilidades consiste en: Si un experimento puede dividirse en N eventos posibles, igualmente verosímiles, entonces cada evento tiene probabilidad 1/N. En el caso del dado, como obtener cualquier cara es igualmente verosímil, la probabilidad de cualquiera de ellas es 1/6.
3) Finalmente, la probabilidad puede asignarse de manera subjetiva, en función de las creencias. Esto puede parecer menos serio que los otros métodos, pero lo cierto es que rara vez es posible realizar un experimento 60 mil veces o contar con circunstancias en que esté claro cómo separar el espacio de posibilidades en eventos igualmente verosímiles. Dicho esto, no se trata simplemente de asignar probabilidades «a ojo» sino de partir de creencias relativamente sencillas y mejorar nuestras estimaciones utilizando el Teorema de Bayes.
Propiedades de probabilidad
Independientemente del método mediante el cual decidamos asignar una probabilidad a un evento, las leyes de Probabilidad son Teoremas, y lo que construyamos a partir de nuestras estimaciones debe respetarlas.
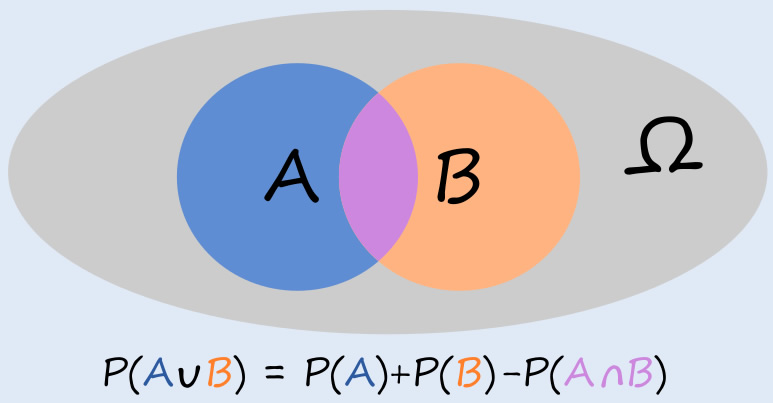
Llamemos Ω al espacio muestral, de todos los posibles resultados que pueden obtenerse a partir de cierto experimento. Entones, un evento A se define como un subconjunto de Ω, y se cumplen las siguientes propiedades:
1) \($P(\Omega) = 1\) . Es decir que la probabilidad de que ocurra un resultado cualquiera entre todos los posibles es 1.
2) \(P(A^c) = 1-P(A)\) , donde \(\cdot^c\) denota el complemento. Esto quiere decir que la probabilidad de que no ocurra un evento A es igual a uno menos la probabilidad de que sí ocurra.
3) La probabilidad de que ocurra A o B está dada por \(P(A\cup B) = P(A)+P(B)-P(A\cap B)\), donde \(P(A\cap B)\) es la probabilidad de que ocurran ambos en simultáneo.
4) Si dos eventos A y B son independientes (ninguno influye en el otro), entonces \(P(A\cap B) = P(A)P(B)\) .
5) Si dos eventos A y B son mutuamente excluyentes (no pueden ocurrir simultáneamente), entonces \(P(A\cap B) = 0\) .
6) Si dos eventos A y B son mutuamente excluyentes, entonces la probabilidad de que ocurra alguno \(P(A\cup B) = P(A) + P(B)\) .
7) Probabilidad condicional: La probabilidad de que ocurra un evento A dado que ocurrió B está dada por \(P(A|B) = P(A\cap B)/P(B)\) ,
8) Teorema de Bayes: \(P(A|B) = P(B|A)P(A)/P(B)\) .
Experimento: distribución de probabilidad
A un experimento dado podemos asignarle una distribución de probabilidad. Habiendo definido los posibles resultados en términos de variables numéricas, una distribución de probabilidad es una función que indica qué probabilidad le corresponde a cada una de ellas.
Esto permite calcular la probabilidad de un evento a partir de integrar (o sumar, para el caso discreto) la función de distribución sobre los resultados que corresponden a tal evento. Existen varias distribuciones que podemos asignarle a un experimento según las circunstancias, y que son utilizadas regularmente para el modelado de datos.

Trabajo publicado en: Feb., 2021.