Definición de Proporcionalidad (Directa e Inversa)

Maestría en Matemáticas, Dr. en Ciencias
1. Parte o segmento constitutivo de un todo que permite calcularse a nivel matemático.
2. Dimensiones que configura cada elemento de una composición.
3. Acuerdo en las formas en que se asigna o distribuye un conjunto de elementos representados por su unidad.
Etimología: Por las formas del latín proportionalĭtas, proportionalĭtātis, respecto de proportionālis, de proportio, proportiōnis, formado por el prefijo pro-, en cuanto ‘hacia’, ‘adelante’, y los modos portio, portiōnis, que remiten a ‘porción’.
Cat. gramatical: Sustantivo fem.
En sílabas: pro-por-cio-na-li-dad.
Proporcionalidad (Directa e Inversa)
A instancias de las matemáticas, la proporcionalidad es la conformidad o proporción (igualdad de dos razones) de unas partes con el todo o de elementos vinculados entre sí , o más formalmente, resulta ser la relación entre magnitudes medibles, dentro de los cual existen dos categorías: directa e inversa.
Se dice que la variable \(y\) es directamente proporcional con la variable \(x\) si existe una constante \(k,\) tal que:
\(y = kx\)
La constante \(k\) es llamada constante de proporcionalidad.
Se dice que la variable \(y\) es inversamente proporcional con la variable \(x\) si existe una constante \(k,\) tal que:
\(yx = k\)
La constante \(k\) es llamada constante de proporcionalidad inversa.
Cuando \(x \ne 0\), podemos despejar a \(y:\)
\(y = \frac{k}{x} = k\left( {\frac{1}{x}} \right)\)
De lo anterior se concluye que la variable \(y\) es directamente proporcional con el inverso multiplicativo de la variable \(x\). Al despejar \(x\) nos percatamos que es directamente proporcional con el inverso multiplicativo de \(y\). En ambos casos la constante de proporcionalidad es la misma, a saber: \(k.\)
Ejemplos de proporcionalidad directa
Ejemplo práctico 1: Costos
Al comprar gasolina, la cantidad a pagar es directamente proporcional a la cantidad de litros y la constante de proporcionalidad es el precio por litro:
\(y = px\)
Donde \(x\) es la cantidad de litros, \(p\) es el precio por litro e \(y\) es la cantidad por pagar.
Si el precio por litro de la gasolina es de $20.30
1. Determine la cantidad por pagar si se compran 12 litros
2. ¿Cuántos litros de gasolina se pueden comprar con $350?
Solución
1. En este caso
\(y = 20.30x\)
Al sustituir \(x = 12:\)
\(y = 20.3\left( {12} \right) = 243.6\)
2. Al sustituir \(y = 350,\;\)al resolver la ecuación
\(350 = 20.3\left( x \right)\)
\(x = \frac{{350}}{{20.3}} = 17.241\)
Ejemplo práctico 2: Física
Cuando un automóvil viaja a velocidad constante; la distancia recorrida es directamente proporcional al tiempo y en este caso; la velocidad es la constante de proporcionalidad:
\(d = vt\)
En donde \(d\) es la distancia, \(v\) es la velocidad y \(t\) es el tiempo.
Un automóvil viaja a velocidad constante a 60 km/h ¿cuánto tiempo tardará en recorrer 150 km?
Solución
Al sustituir \(d\)=150 y \(v = 60\):
\(150 = 60t\)
\(t = \frac{{150}}{{60}} = \frac{5}{2}\)
Tardará 2 horas y media.
Razones y proporciones
Una razón es el cociente de dos números, con el divisor distinto de cero; es decir:
\(\frac{a}{b}\;{\rm{con\;}}b \ne 0\)
Una proporción es la igualdad de dos razones, es decir:
\(\frac{a}{b} = \frac{c}{d} = k,\)
\(k\) es llamada, también, constante de proporcionalidad.
Propiedades de las proporciones
Si \(\frac{a}{b} = \frac{c}{d} = k\) entonces para \(m \ne 0:\;\)
\(\frac{{ma}}{{mb}} = \frac{a}{b} = \frac{c}{d} = k\)
\(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a – c}}{{b – d}} = k\)
\(\frac{a}{b} = \frac{c}{d} = \frac{f}{g} = \frac{{a + c + f}}{{b + d + g}} = k\)
Ejemplo
\(\frac{9}{{21}} = \frac{{15}}{{35}} = \frac{{9 + 15}}{{21 + 35}} = \frac{{24}}{{56}}\)
\(\frac{9}{{21}} = \frac{{15}}{{35}} = \frac{{15 – 9}}{{35 – 21}} = \frac{6}{{14}}\)
Regla de tres simple directa
La regla de tres simple permite resolver, de una manera práctica, problemas relacionados con relaciones directamente proporcionales y con proporciones sin necesidad de conocer la constante de proporcionalidad de manera explícita. Para poder aplicarla se requiere conocer dos variables que sean directamente proporcionales y otra de cualquiera de esas mismas variables
Si en una relación directamente proporcional se tiene:
\(c = ak\)
\(d = bk\)
Entonces podemos establecer la proporción:
\(\frac{a}{b} = \frac{c}{d}\)
En consecuencia:
\(ad = bc\)
Al despejar las literales \(b\) y \(d\), se obtiene:
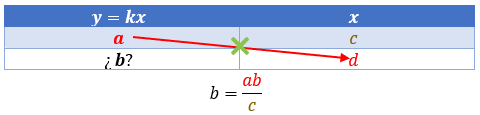
\(b = \frac{{ad}}{c}\)
\(d = \frac{{bc}}{a}\)
Esquema de la regla de 3 simple
Si \(y = kx\), con \(k\) la constante de proporcionalidad
Para cuando se desconoce, \(d\)
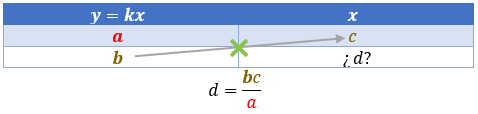
Para cuando se desconoce, \(b\)
Ejemplo práctico 3: Cambio de unidades
Una persona al intercambiar pesos por euros; pagó 1736 pesos por 70 euros.
1. Si sólo hubiera comprado 50 euros ¿cuánto hubiera pagado?
2. ¿Para cuántos euros se pueden comprar con $2000?
Solución
1.

\(b = \frac{{\left( {1736} \right)\left( {50} \right)}}{{70}} = 1240\)
Se pagarían 1240 pesos al comprar 50 euros
2.

\(d = \frac{{\left( {2000} \right)\left( {70} \right)}}{{1736}} = \frac{{2500}}{{31}} = 80.645\)
Con 2000 pesos se pueden comprar 80.645 euros.
Representación Geométrica
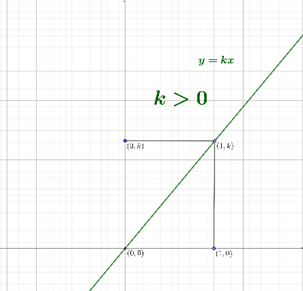
Gráfica de y = kx , Caso k > 0
| \(x\) | \(y = kx\) |
|---|---|
| 0 | 1 |
| 0 | \(k\) |
La gráfica es una recta que pasa por los puntos \(\left( {0,0} \right)\) y \(\left( {1,k} \right)\). En este caso \(y = kx\) es una función creciente.
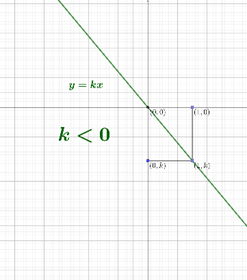
Caso \(k < 0\)
| \(x\) | \(y = kx\) |
|---|---|
| 0 | 1 |
| 0 | \(k\) |
La gráfica es una recta que pasa por los puntos \(\left( {0,0} \right)\) y \(\left( {1,k} \right).\)
En este caso, \(y = kx,\) es una función decreciente.
Reparto proporcional
Se dice que las cantidades \(G\) y \(A\) se han repartido en partes proporcionales si
\(\frac{{{g_1}}}{{{a_1}}} = \frac{{{g_2}}}{{{a_2}}} = \frac{{{g_3}}}{{{a_3}}} = \ldots = \frac{{{g_n}}}{{{a_n}}} = \frac{{{g_1} + {g_2} + {g_3} + \ldots + {g_n}}}{{{a_1} + {a_2} + {a_3} + \ldots + {a_n}}} = \frac{G}{A} = k\;\)
Donde
\({g_1} + {g_2} + {g_3} + \ldots + {g_n} = G\)
\({a_1} + {a_2} + {g_3} + \ldots + {a_n} = A\)
Ejemplo de reparto proporcional
Con el propósito de exportar su cosecha de café, varios campesinos reunieron su cosecha y obtuvieron una ganancia de $140000, que repartirán de manera justa (proporcionalmente a la cantidad de toneladas aportadas). Encuentra la cantidad de dinero que le corresponde a cada campesino; en la tabla están indicadas las toneladas con las que contribuyó cada uno.
| Total | \(k\) | |||||||
|---|---|---|---|---|---|---|---|---|
| Ganancia por obtener | \(b\) | \(a\) | \(c\) | \(d\) | \(e\) | \(f\) | 140000 | \(\frac{G}{A}\) |
| Contribución | 8 | 5 | 6 | 2 | 3 | 4 | \(\frac{G}{A}\) |
Solución
La cantidad de toneladas vendidas fue de \(8 + 5 + 6 + 2 + 3 + 4 = 28\), como la ganancia total fue de $140000; entonces la ganancia por cada tonelada es igual a:
\(\frac{G}{A} = \frac{{140000}}{{28}} = 5000\)
Como \(\frac{a}{8} = 5000\); podemos garantizar \(a = 40000\).
De manera análoga se puede calcular las demás ganancias para el resto de los campesinos; las cuales se muestran en la siguiente tabla.
| Total | \(k\) | |||||||
|---|---|---|---|---|---|---|---|---|
| Ganancia por obtener | \(40000\) | \(25000\) | \(30000\) | \(10000\) | \(15000\) | \(20000\) | 140000 | \(\frac{G}{A} = 5000\) |
| Contribución | 8 | 5 | 6 | 2 | 3 | 4 | 28 | \(\frac{G}{A} = 5000\) |
Ejemplos de proporcionalidad inversa
Áreas constantes: Ejemplo práctico 1
El área de un rectángulo es igual a la base por su altura:
\(A = bh\)
Donde \(b\) es la base del rectángulo, \(h\) su altura y \(A\) su área.
Si queremos construir un rectángulo de 24 cm2 se establece
\(bh = 24\)
Lo anterior indica que la base y la altura están relacionadas de manera inversamente proporcional y la constante es \(k = 24\).
Si se conoce el valor de la base podemos calcular la altura del siguiente modo:
\(h = \frac{{24}}{b}\)
La siguiente tabla muestra diferentes valores de la base (b) y de la altura (\(h = \frac{{24}}{b}\) ) para que el rectángulo tenga un área de 24 cm
| Base (b) | Altura (\(h = \frac{{24}}{b}\)) |
|---|---|
| \(\frac{1}{3}\) | 72 |
| \(\frac{1}{2}\) | 48 |
| 1 | 24 |
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
| 6 | 4 |
| 8 | 8 |
| 12 | 2 |
| 24 | 1 |
| 48 | \(\frac{1}{2}\) |
| 72 | \(\frac{1}{3}\) |
Gráfica: Altura vs Base
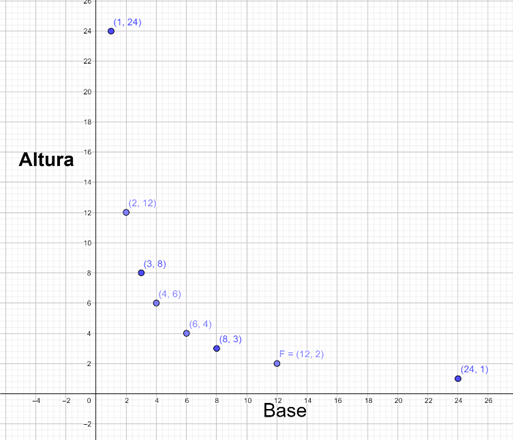
Física: Ejemplo práctico 2
Se necesita recorrer una distancia de 60 km y partir de la fórmula
\(d = vt\)
En donde \(d = 60\;{\rm{km}}\) (en este caso) es la distancia, \(v\) es la velocidad y \(t\) es el tiempo:
\(60 = vt\)
De lo anterior concluimos que hay una relación inversamente proporcional entre la velocidad y el tiempo, al despejar t, se obtiene:
\(t = \frac{{60}}{v}\)
La siguiente tabla muestra el tiempo \(t\) (en horas) que se requiere para recorrer una distancia de 60 km para para diferentes velocidades \(v\) (en km/hora).
| Velocidad (\(v\)) | tiempo(t\( = \frac{{60}}{v}\)) |
|---|---|
| 5 | 12 |
| 10 | 6 |
| 15 | 4 |
| 20 | 3 |
| 30 | 2 |
| 45 | \(\frac{4}{3}\) |
| 60 | 1 |
| 90 | \(\frac{2}{3}\) |
Gráfica: Tiempo vs Velocidad
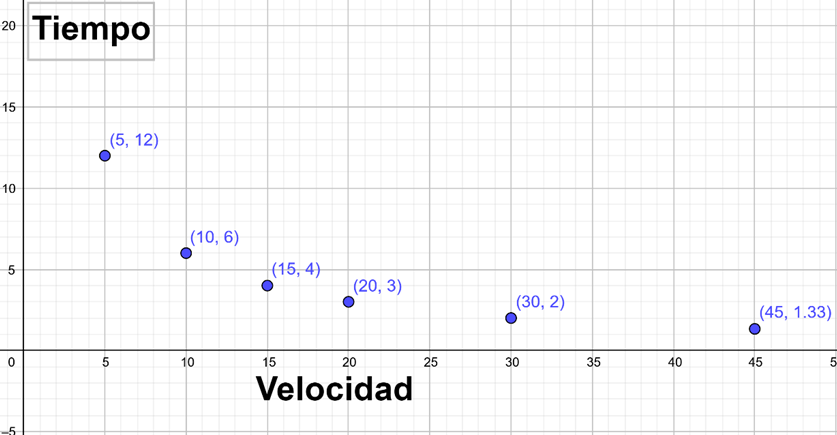
Trabajo: Ejemplo práctico 3
Se necesitan imprimir 5400 páginas y se cuenta con tres impresoras una que imprime a 15 páginas por minuto, otra a 18 y la más veloz a 30 páginas por minuto.
1. ¿Cuánto tiempo tardará, en imprimir las 5400 páginas cada una de las impresoras?
2. ¿En cuánto tiempo se imprimen las 5400 páginas si se usan, de manera simultánea, la impresora más lenta con las más rápida?
3. ¿En cuánto tiempo se imprimen las 5400 páginas si se usan, de manera simultánea, la impresora más lenta con la segunda más rápida?
4. ¿Con los recursos que se cuentan se pueden imprimir en menos de hora y media?
Solución
De manera análoga a la fórmula de distancia con velocidad y tiempo, tendremos:
\(P = vt\)
\(t = \frac{P}{v}\)
donde \(t\) es tiempo, \(v\), es la velocidad de páginas y \(P\) es la cantidad de páginas.
1. \(t = \frac{{5400}}{{15}} = 360\).
\(t = \frac{{5400}}{{18}} = 300\).
\(t = \frac{{5400}}{{30}} = 180\).
Respuesta: 360 minutos, 300 minutos y 180 minutos; tardarán las impresoras de las más lenta a la más rápida, respectivamente
2. Si se usan la más lenta con la más rápida de manera simultánea entonces se imprimen a 45 páginas por minuto:
\(t = \frac{{5400}}{{45}} = 120\)
Respuesta 120 minutos
3. Si se usan la más rápida con la segunda más rápida de manera simultánea entonces se imprimen a 48 páginas por minuto:
\(t = \frac{{5400}}{{48}} = \frac{{225}}{2} = 112.5\)
Respuesta 112.5 minutos
4. Se tiene:
\(v = \frac{{5400}}{t}\)
Como hora y media es igual a 90 minutos:
\(v = \frac{{5400}}{{90}} = 60\)
Se requiere que pueda imprimir a más de 60 páginas por minuto para lograr imprimir 5400 páginas en menos de 90 minutos y esto se logra, imprimiendo con las tres impresoras de manera simultánea
Ejemplo práctico 4
Una persona, tarda 3 horas en hacer cierto trabajo y otra persona tarda 2 horas ¿En cuánto tiempo harán el mismo trabajo si trabajan de forma simultánea?
Solución
En una hora un trabajador avanza \(\frac{1}{3}\) del trabajo y la otra persona avanza \(\frac{1}{2}\) del trabajo; al trabajar de manera simultánea se avanza:
\(\frac{1}{3} + \frac{1}{2} = \frac{5}{6}\)
En este caso 1 representa el trabajo total y:
\(1 = vt\)
\(1 = \left( {\frac{5}{6}} \right)t\)
\(t = \left( {\frac{6}{5}} \right)\)
Respuesta \(\frac{6}{5}\) de hora.
Regla de tres inversa
La regla de tres inversa permite resolver, de una manera práctica, problemas relacionados con relaciones inversamente proporcionales sin necesidad de conocer la constante de proporcionalidad de manera explícita. Para poder aplicarla se requiere conocer dos variables que sean inversamente proporcionales y otra de cualquiera de esas mismas variables
Si en una relación directamente proporcional se tiene:
\(k = ab\)
\(k = cd\)
Entonces podemos establecer la proporción:
En consecuencia:
\(ab = cd\)
Al despejar las literales \(b\) y \(d\), se obtiene:
\(c = \frac{{ab}}{d}\)
\(d = \frac{{ab}}{c}\)
Esquema de la regla de 3 simple
Si \(yx = k\), con \(k\) la constante de proporcionalidad
Para cuando se desconoce, \(d\)
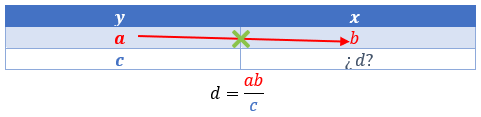
Para cuando se desconoce, \(c\)
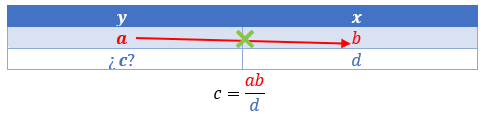
Ejemplo práctico 5
Una impresora que imprime a 22 páginas por minuto tardó 45 minutos en imprimir un documento
1. ¿Cuánto tiempo tardará una impresora que imprime a 18 páginas por minuto?
2. Una impresora tardó 33 minutos en imprimir, al mismo documento, ¿A qué velocidad imprime?
Solución

\(d = \frac{{\left( {22} \right)\left( {45} \right)}}{{18}} = 55\)
Tardaría 55 minutos.
2.

\(c = \frac{{\left( {22} \right)\left( {45} \right)}}{{33}} = 30\)
Imprimió a 30 páginas por minuto.
Reparto inversamente proporcional
Se dice la cantidad \(G\) se ha repartido de manera inversamente proporcional con la cantidad \(A\) si se reparte de manera directamente proporcional con los inversos multiplicativos de la cantidad A, es decir si
\(\frac{{{g_1}}}{{\frac{1}{{{a_1}}}}} = \frac{{{g_2}}}{{\frac{1}{{{a_2}}}}} = \frac{{{g_3}}}{{\frac{1}{{{a_3}}}}} = \ldots = \frac{{{g_n}}}{{\frac{1}{{{a_n}}}}} = \frac{{{g_1} + {g_2} + {g_3} + \ldots + {g_n}}}{{\frac{1}{{{a_1}}} + \frac{1}{{{a_2}}} + \frac{1}{{{a_3}}} + \ldots + \frac{1}{{{a_n}}}}} = \frac{G}{A} = k\;\)
Ahora:
\(\frac{{{g_t}}}{{\frac{1}{{{a_t}}}}} = k\)
\({a_t}{g_t} = k\)
Donde
\({g_1} + {g_2} + {g_3} + \ldots + {g_n} = G\)
\(\frac{1}{{{a_1}}} + \frac{1}{{{a_2}}} + \frac{1}{{{a_3}}} + \ldots + \frac{1}{{{a_n}}} = A\)
Ejemplo práctico 6
Una madre de familia ha recibido una gratificación anual de $47000 y quiere crear tres fondos educativos para los estudios de sus tres descendientes, cuyas edades son 12, 14 y 20 años. Debido a que ya se ha invertido más dinero en la educación del mayor que del menor; ha decido repartir su gratificación de manera inversamente proporcional a las edades de sus descendientes.
Determine la cantidad de cada fondo de inversión.
Solución
| Total | \(k\) | ||||
|---|---|---|---|---|---|
| Dinero para el fondo educativo | \(a\) | \(b\) | \(c\) | 47000 | \(\frac{G}{A} = \frac{{47000}}{{\frac{{47}}{{240}}}} = 240000\) |
| Inverso de la edad | \(\frac{1}{{12}}\) | \(\frac{1}{{{{16}_{}}}}\) | \(\frac{1}{{{{20}_{}}}}\) | \(A = \frac{1}{{12}} + \frac{1}{{16}} + \frac{1}{{20}} = \frac{{47}}{{240}}\) | \(\frac{G}{A} = \frac{{47000}}{{\frac{{47}}{{240}}}} = 240000\) |
Se debe cumplir:
\(\frac{a}{{\frac{1}{{12}}}} = 240000\)
\(12a = 240000\)
\(a = \frac{{24000}}{{12}} = 20000\)
De manera similar se obtiene:
\(b = \frac{{240000}}{{16}} = 15000\)
\(c = \frac{{240000}}{{20000}} = 12000\)
| Total | \(k\) | ||||
|---|---|---|---|---|---|
| Dinero para el fondo educativo | \(24000\) | \(15000\) | \(12000\) | \(47000\) | \(\frac{G}{A} = \frac{{47000}}{{\frac{{47}}{{240}}}} = 240000\) |
| Inverso de la edad | \(\frac{1}{{12}}\) | \(\frac{1}{{{{20}_{}}}}\) | \(\frac{1}{{{{20}_{}}}}\) | \(A = \frac{1}{{12}} + \frac{1}{{16}} + \frac{1}{{20}} = \frac{{47}}{{240}}\) | \(\frac{G}{A} = \frac{{47000}}{{\frac{{47}}{{240}}}} = 240000\) |
Representación geométrica de una relación inversamente proporcional
Gráfica de \(xy = k\;\) con \(k > 0\)
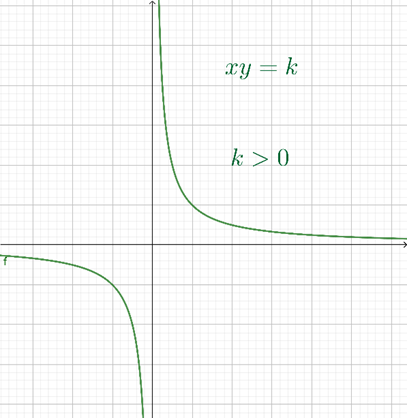
Gráfica de \(xy = k\;\) con \(k < 0.\)
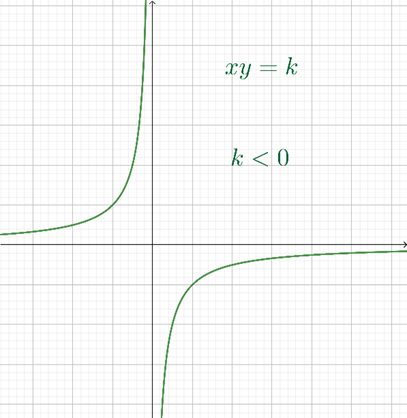

Art. actualizado: Nov. 2022; sobre el original de octubre, 2011.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.