Significado de rectas paralelas y perpendiculares Definición, diferencia, ejemplos, y ejercicios

Licenciada en Física
Definición formal
Las rectas paralelas sobre el plano son aquellas que forman entre sí un ángulo de 0º y guardan cierta distancia entre sí, ya que cuando se superponen una a la otra, se llaman rectas coincidentes. Por su parte, la diferencia de las rectas perpendiculares radica en que estas forman un ángulo de 90º y tienen un punto de intersección.
Tanto las rectas paralelas como las perpendiculares forman parte de la geometría los objetos cotidianos, las construcciones, las calles y mucho más, de allí que su estudio sea tan relevante.
En términos de la pendiente de la recta, que representa la inclinación de la misma respecto a la horizontal, dos rectas son paralelas cuando tienen la misma pendiente. De esta manera, el ángulo que forman con el eje horizontal es el mismo, como se muestra en siguiente figura, donde este ángulo se llama α:
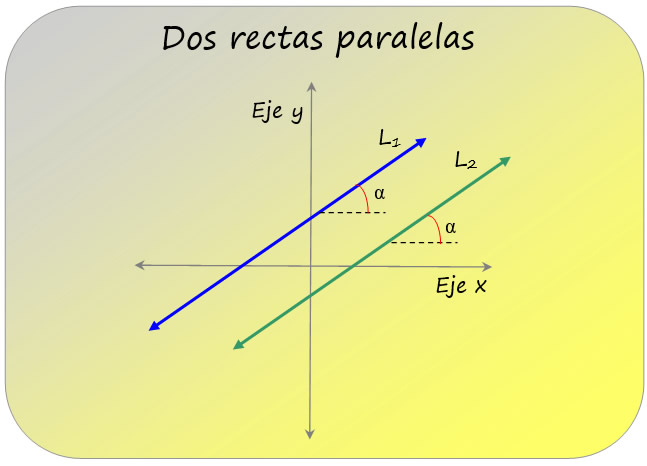
Por supuesto, dos rectas verticales separadas siempre son paralelas.
En cuanto a las rectas perpendiculares, ellas pueden formar cualquier ángulo con el eje horizontal, con la condición de que entre ambas el ángulo sea 90º. En la siguiente figura hay dos rectas L1 y L2, las cuales forman ángulos α y β respectivamente con la horizontal, el ángulo entre ellas dos es 90º y tienen un punto de intersección, son por lo tanto perpendiculares.
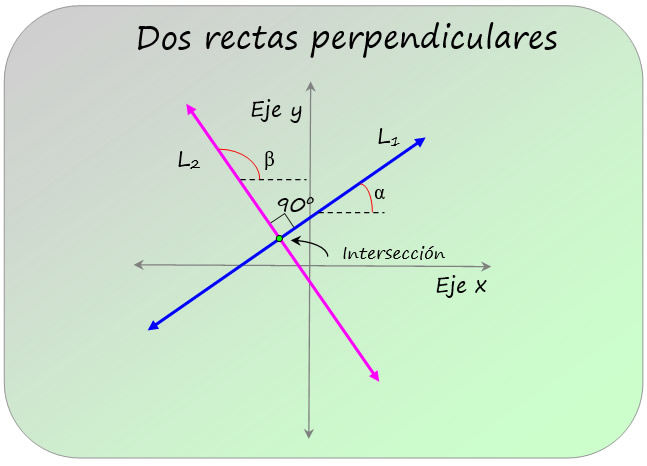
Criterio de las pendientes para las rectas paralelas y perpendiculares
Una recta se puede expresar en forma matemática mediante la ecuación:
y = mx + b
Donde b es el corte de la recta con el eje vertical y m es la pendiente, relacionada con el ángulo α que forma la recta con la horizontal mediante:
m = tg α
Las pendientes de las rectas paralelas y las pendientes de las rectas perpendiculares cumplen entre sí determinadas condiciones, que se describen de inmediato.
Ejemplos de rectas paralelas
Sea la recta L1 cuya ecuación es:
y1 = m1x + b1
Y la recta L2 de ecuación:
y2 = m2x + b2
Ambas son paralelas si:
m1 = m2
Es decir, tienen la misma inclinación y forman el mismo ángulo α con la horizontal. Si además b1 = b2, las rectas son coincidentes.
Por ejemplo, las rectas:
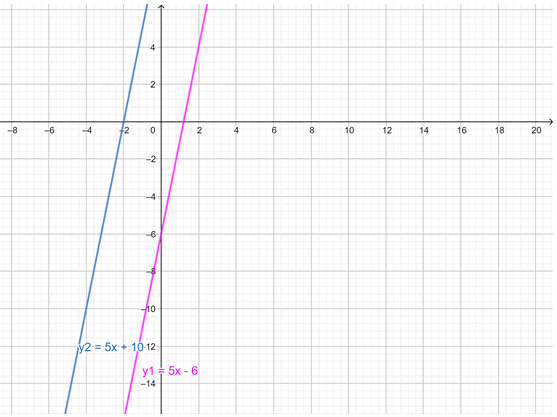
L1: y = 5x − 6
L2: y = 5x + 10
Son paralelas, ya que m1 = m2 =5 y b1 = − 6 es diferente de b2 = 10. Sus gráficas se muestran a continuació:
Ejemplos de rectas perpendiculares
Supóngase las rectas L1 y L2 cuyas respectivas ecuaciones son:
y1 = m1x + b
y2 = m2x + b
Se dice que L1 y L2 son perpendiculares si cumplen la siguiente condición:
\(m{}_{1}=-\frac{1}{{{m}_{2}}}\)
Esta ecuación también se puede escribir así:
m1∙m2 = −1
Y los respectivos ángulos que forman con la horizontal se relacionan a través de:
β − α = 90º
Como ejemplo se tienen las siguientes rectas:
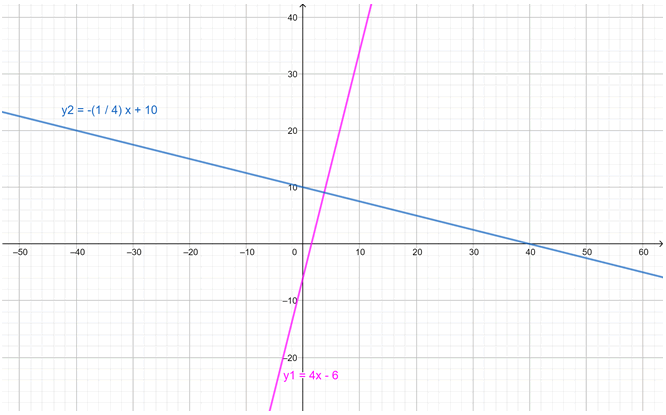
L1: y = 4x − 6
L2: y = (−1/4)x + 10
Ambas son perpendiculares, ya que m1 = 4, m2 = −1/4 y el producto de ambas es:
m1∙m2 = 4∙(−1/4) = −1
Ejercicios de aplicación
Ejercicio 1: Determinar si las siguientes rectas son paralelas, perpendiculares o ninguna de las dos opciones:
L1: 4y -5x +1 = 0
L2: 8y -10x −7= 0
Respuesta
Para aplicar el criterio de las pendientes, conviene expresar cada recta de la forma y = mx + b y esto se consigue despejando la y en cada caso:
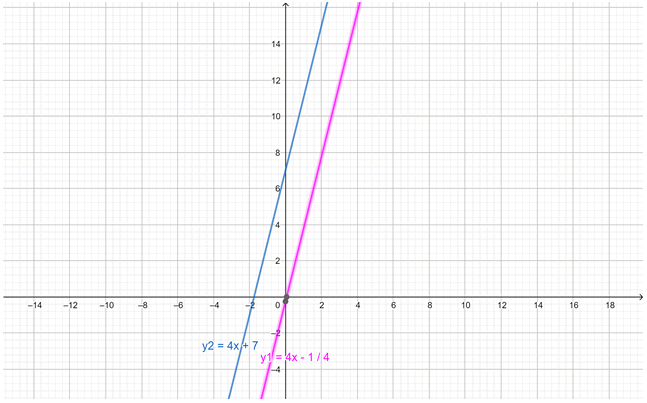
L1: 4y −16x +1 = 0 \(\Rightarrow y=\frac{16x}{4}-\frac{1}{4}=4x-\frac{1}{4}\)
L2: y −4x −7= 0 \(\Rightarrow y=4x+7\)
Las rectas son paralelas, puesto que ambas tienen la misma pendiente m = 4 y se comprueba graficando.
Ejercicio 2: Hallar la ecuación de la recta que pasa por el punto P(−4, \(\frac{\text{5}}{\text{2}}\text{)}\) y es perpendicular a la recta de ecuación 3x –y – 4 =0.
Respuesta
Se busca determinar la ecuación de la recta L1 que pasa por el punto P, y que sea perpendicular a la recta L2 cuya ecuación se tiene. El primer paso es determinar la pendiente de L2:
L2: \(\text{3x-y-4}=\text{0}\Rightarrow \text{y }=\text{3x-4}\)
Por lo tanto la pendiente de L2 es:
m2 = 3
Como se requiere que L1 y L2 sean perpendiculares, se cumple que:
m1∙m2 = −1
Sustituyendo m2 = 3:
3m1 = −1\(\Rightarrow {{\text{m}}_{\text{1}}}=-\frac{\text{1}}{\text{3}}\)
Ya se tiene la pendiente m1, por lo tanto la ecuación de L1 es:
L1: \(\text{y }=-\frac{\text{1}}{\text{3}}x+b\)
Falta determinar el valor de b, esto se logra sustituyendo el punto P(−4, \(\frac{\text{5}}{\text{2}}\text{)}\), puesto que el enunciado dice que pertenece a L1:
\(\frac{\text{5}}{\text{2}}\text{ }=-\frac{\text{1}}{\text{3}}\text{(-4)}+b\Rightarrow \frac{\text{5}}{\text{2}}=\frac{\text{4}}{\text{3}}+b\Rightarrow \text{b}=\frac{\text{7}}{\text{6}}\)
Finalmente la ecuación buscada es:
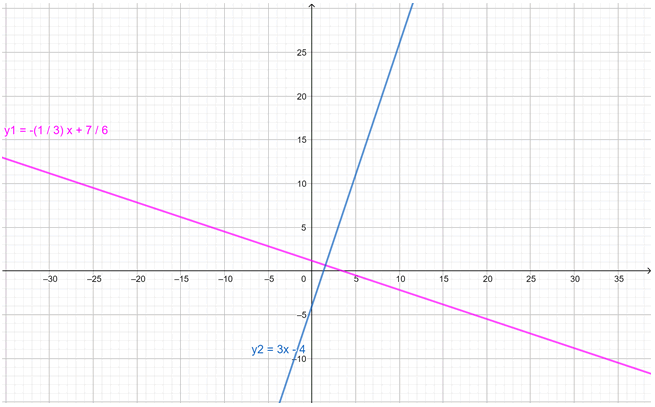
L1: \(\text{y }=-\frac{\text{1}}{\text{3}}x+\frac{7}{6}\)
La gráfica de ambas rectas se muestra a continuación:

Trabajo publicado en: Ene., 2021.