Definición de Refracción

Ángel Zamora Ramírez
Licenciado en Física

La refracción es el cambio en la dirección de propagación de una onda cuando esta pasa de un medio con cierto índice de refracción a otro medio con un índice de refracción distinto.

El fenómeno de refracción ocurre con distintos tipos de ondas, no obstante, el más observado es el de la luz, en cuyo caso se aprecia introduciendo un objeto largo como un popote o una pajilla en un vaso de vidrio con agua. Al observar a través del vaso pareciera que el objeto se “dobla”, lo cual se debe a que la luz reflejada por la porción del popote sumergida en agua tiene una dirección diferente a la luz reflejada por la porción que se encuentre fuera del agua. El aire y el agua tienen índices de refracción distintos, lo cual es lo que crea esta ilusión óptica.
pajilla

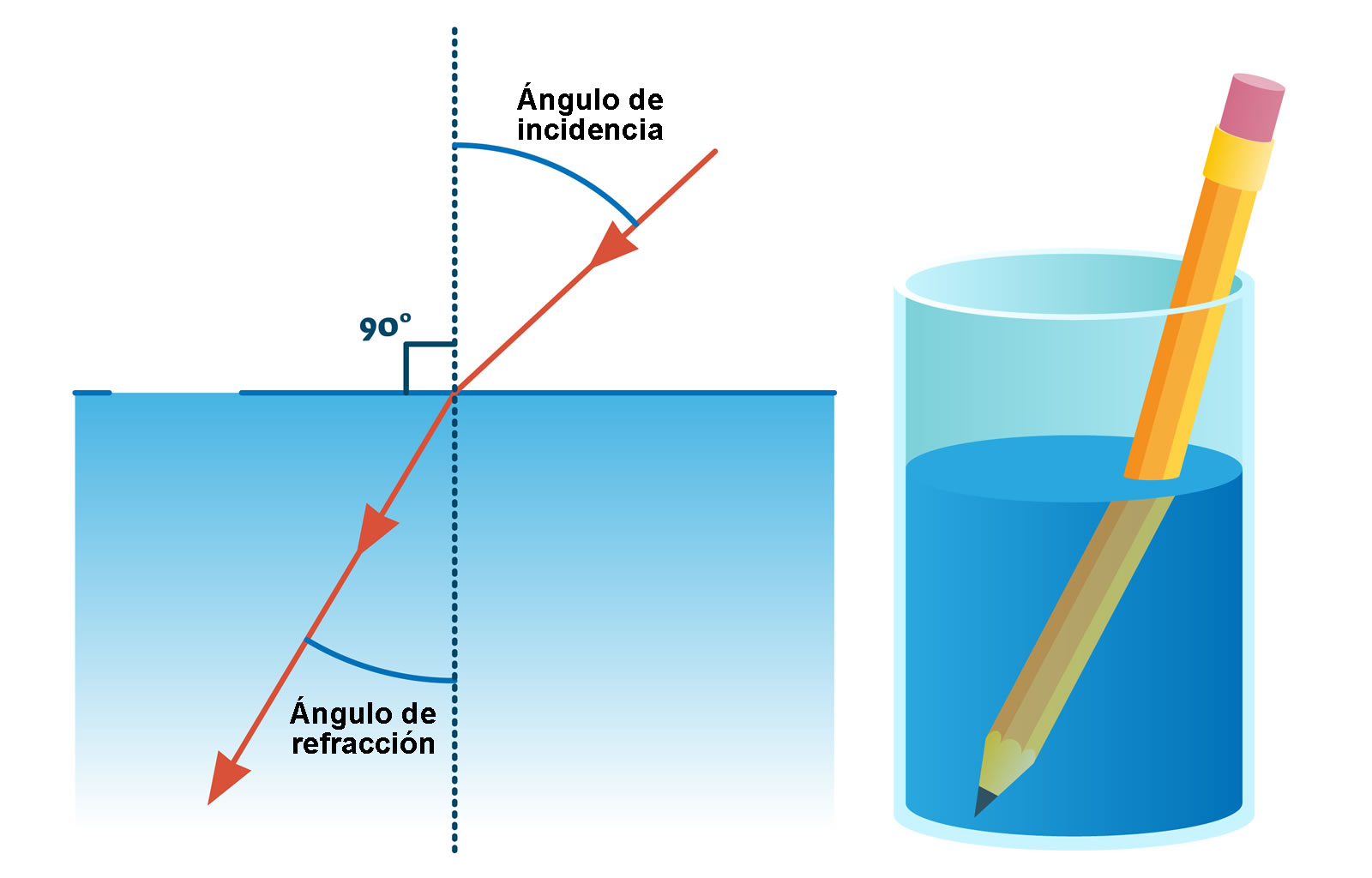
Índice de refracción de la luz

La velocidad a la cual se propaga la luz en un medio depende de la permitividad eléctrica y la permeabilidad magnética de dicho medio. En el vació la luz se propaga a una velocidad dada por:

\(c = \frac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}\)

Donde \(c\) es la velocidad de la luz en el vació, \({\mu _0}\) es la permeabilidad magnética del vació y \({\varepsilon _0}\) es la permitividad eléctrica del vació. Esto es para el vacío, pero, ¿Cómo es la velocidad de la luz en otro medio distinto al vacío? Para ello necesitamos utilizar la permitividad eléctrica de dicho medio (\(\varepsilon \)) y su permeabilidad magnética (\(\mu \)). En ese medio la velocidad \(v\) a la cual se propaga la luz sería:

\(v = \frac{1}{{\sqrt {\mu \varepsilon } }}\)

La relación entre la permitividad eléctrica y la permeabilidad magnética de ese medio con las del vacío son las siguientes: \(\varepsilon = {\varepsilon _r}{\varepsilon _0}\), \(\mu = {\mu _r}{\mu _0}\). Donde \({\varepsilon _r}\) y \({\mu _r}\) son la permitividad relativa y la permeabilidad relativa, respectivamente. Sustituyendo esto en la última ecuación obtenemos que la velocidad de propagación de la luz en ese medio sería:

\(v = \frac{1}{{\sqrt {{\mu _r}{\mu _0}{\varepsilon _r}{\varepsilon _0}} }} = \frac{1}{{\sqrt {{\mu _r}{\varepsilon _r}} }}\frac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}\)

Esto último, utilizando la definición de la velocidad de la luz en el vacío (\(c\)), lo podemos escribir como:

\(v = \frac{c}{{\sqrt {{\mu _r}{\varepsilon _r}} }}\)

O bien, también podemos decir que:

\(\frac{c}{v} = \sqrt {{\mu _r}{\varepsilon _r}} \)

El índice de refracción de la luz en un medio se define como el cociente entre la velocidad de la luz en el vació y la velocidad de luz en dicho medio. Sea \(\eta \) el índice de refracción, utilizando la última ecuación podemos decir que:

\(\eta = \frac{c}{v} = \sqrt {{\mu _r}{\varepsilon _r}} \)

Es decir, el índice de refracción de un medio depende de su permitividad eléctrica relativa y su permeabilidad magnética relativa. Tanto \({\varepsilon _r}\) como \({\mu _r}\) son cantidades adimensionales con valores mayores a 1, por lo tanto \(\eta > 1\). Entre mayores sean la permitividad relativa y permeabilidad relativa de un medio, mayor será su índice de refracción.

Ley de Snell

Anteriormente se mencionó que cuando una onda como la luz pasa de un medio a otro, ambos con índices de refracción distintos, la dirección de propagación cambia. La ley que describe este fenómeno se conoce como “Ley de Snell” y fue formulada por el matemático neerlandés Willebrord Snel van Royen. Supongamos que tenemos dos medios con índices de refracción \({\eta _1}\) y \({\eta _2}\), un rayo de luz viaja a través del medio con \({\eta _1}\) e incide en la frontera de ambos medios con un ángulo \({\theta _1}\), posteriormente, el rayo de luz pasa al medio con \({\eta _2}\) y es refractado con un ángulo \({\theta _2}\). La ley de Snell postula que:

\({\eta _1}\sin {\theta _1} = {\eta _2}\sin {\theta _2}\)

O bien:

\(\frac{{{\eta _1}}}{{{\eta _2}}} = \frac{{\sin {\theta _2}}}{{\sin {\theta _1}}}\)

Notemos que si \(\theta = 0\) no existe refracción independientemente de los índices de refracción. Aparte de esto, podemos analizar tres casos particulares:

Si \({\eta _1} = {\eta _2}\) entonces \({\theta _1} = {\theta _2}\). Si ambos medios tienen el mismo índice de refracción el rayo de luz no cambia su dirección.

Si \({\eta _1} > {\eta _2}\) entonces \({\theta _1} < {\theta _2}\). En este caso el rayo de luz es desviado “hacía afuera” de la dirección de incidencia.

Si \({\eta _1} < {\eta _2}\) entonces \({\theta _1} > {\theta _2}\). En este caso el rayo de luz es desviado “hacía adentro” de la dirección de incidencia.

Refracción y dispersión

Quizá muchos de nosotros estamos familiarizados con la portada del álbum “The Dark Side of the Moon” de la banda británica “Pink Floyd”. Esta imagen a su vez está basada en el famoso experimento de Newton en el que dispersó con un prisma la luz blanca proveniente del Sol obteniendo los colores del arcoíris. La luz blanca en realidad está compuesta por distintas frecuencias, cada una correspondiente a un color en el espectro de luz visible. El índice de refracción de un medio depende también en parte de la frecuencia de la luz incidente.

Cuando un rayo de luz blanca se pasa a través de un prisma las distintas frecuencias que componen la luz blanca experimentan distintos índices de refracción y por lo tanto se refractan en distintas direcciones, de esta manera todas estas frecuencias se dispersan y revelan el especto de luz visible.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Trabajo publicado en: Ago., 2022.

Datos para citar en modelo APA: Zamora Ramírez, A. (agosto, 2022). Definición de Refracción. Significado.com. Desde https://significado.com/refraccion/