Definición de Trigonometría

Ángel Zamora Ramírez
Licenciado en Física

La trigonometría es una rama de la geometría y de las matemáticas que se encarga del estudio de los triángulos, así como de las relaciones que existen entre sus lados y sus ángulos.

El triángulo es una figura geométrica que durante cientos de años ha intrigado a varias civilizaciones, al punto de ser considerada por muchos la figura perfecta. El desarrollo de la trigonometría es la culminación de varios siglos de estudio de estas figuras geométricas. Aunque en un principio pareciera que la trigonometría se limita al abordaje de los triángulos, la verdad es que los conceptos que se maneja tiene aplicaciones en muchas áreas del conocimiento humano. La trigonometría se utiliza en la medición de distancias, en el análisis de señales, en el modelado matemático, etc.

El triángulo rectángulo y el Teorema de Pitágoras

Para hablar sobre trigonometría quizá debamos empezar por el análisis del triángulo rectángulo. Un triángulo rectángulo es un tipo de triángulo que se caracteriza por poseer un ángulo recto, es decir, un ángulo de 90°.

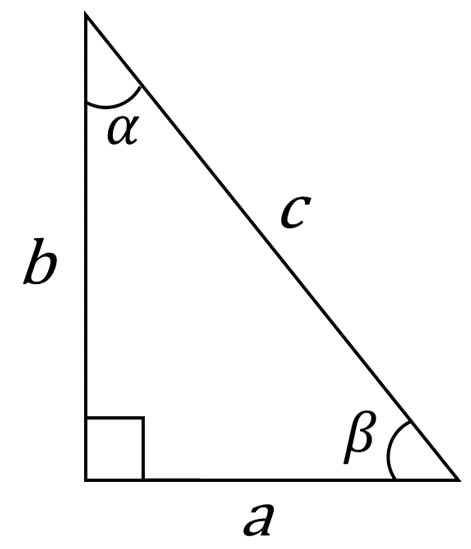
En este triángulo rectángulo, los lados \(a\) y \(b\) cuya unión conforma el ángulo recto son conocidos como “catetos”, el lado restante \(c\) y que es opuesto al ángulo recto se llama “hipotenusa”. Existe una relación matemática entre los tres lados del triángulo rectángulo, la cual establece que:
\({c^2} = {a^2} + {b^2}\)

Este es el ya bastante conocido “Teorema de Pitágoras” el cual nos dice que “en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”.

El triángulo rectángulo y las funciones trigonométricas

Del estudio de los triángulos rectángulos también surgen las “Razones Trigonométricas” que relacionan los ángulos de un triángulo rectángulo con sus catetos y su hipotenusa. Las tres principales razones trigonométricas son el “seno”, el “coseno” y la “tangente”. Estas razones trigonométricas para el ángulo \(\alpha \) del triángulo de la figura anterior estarán dadas por:

\(\sin \alpha = \frac{a}{c},\;\;\cos \alpha = \;\frac{b}{c},\;\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{a}{b}\)

Por su parte, estas mismas razones trigonométricas para el ángulo \(\beta \) serían:

\(\sin \beta = \frac{b}{c},\;\;\cos \beta = \;\frac{a}{c},\;\;\tan \beta = \frac{{\sin \beta }}{{\cos \beta }} = \frac{b}{a}\)

También existe otras razones trigonométricas que dependen de las anteriores y que son llamadas “cosecante”, “secante” y “cotangente”. Estas razones trigonométricas para el ángulo \(\alpha \) estarían dadas por:

\(\csc \alpha = \frac{1}{{\sin \alpha }} = \frac{c}{a},\;\;\sec \alpha = \frac{1}{{\cos \alpha }} = \frac{c}{b},\;\;\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{b}{a}\)

Todas estas razones trigonométricas relacionan los ángulos de un triángulo rectángulo con cocientes entre sus lados, sin embargo, podemos extender la definición de estas razones a todos los números reales y definir las “funciones trigonométricas”.

La variable independiente de una función trigonométrica es un ángulo en radianes, donde 1 radián es el ángulo que abarca un arco de circunferencia cuya longitud es igual a la longitud del radio y tiene un valor aproximado de 57.3°. El valor de una función trigonométrica en un punto dado es el valor que tendría la razón trigonométrica correspondiente para dicho ángulo en radianes.

Funciones trigonométricas inversas

En un principio las razones trigonométricas son de gran utilidad debido a que gracias a estas podemos determinar las medidas de los ángulos de un triángulo rectángulo si conocemos las medidas de sus lados, y viceversa.

Existen funciones que son inversas a las funciones trigonométricas que se mencionaron anteriormente. Las funciones inversas podemos definirlas como:

\(Si\;y = \sin x ⟹ x = {\sin ^{ – 1}}y\)

\(Si\;y = \cos x ⟹ x = {\cos ^{ – 1}}y\)

\(Si\;y = \tan x ⟹ x = {\tan ^{ – 1}}y\)

Las funciones trigonométricas inversas nos dan el valor del ángulo que corresponde a cierto valor de su respectiva razón trigonométrica. Por ejemplo, supongamos que en el triángulo anterior desconocemos la medida del ángulo \(\alpha \), este ángulo puede ser obtenido haciendo uso de las funciones trigonométricas inversas, de tal manera que:

\(\alpha = {\sin ^{ – 1}}\frac{a}{c} = {\cos ^{ – 1}}\frac{b}{c} = {\tan ^{ – 1}}\frac{a}{b}\)

Aplicaciones de las funciones trigonométricas

Una de las aplicaciones más importantes de la trigonometría es la medición de distancias. Un ejemplo claro de esto fue la hazaña del astrónomo y matemático griego Eratóstenes quien en el siglo III a.C. se percató que, durante el mediodía solar del solsticio de verano, en Siena los objetos no proyectaban sombra, cosa contraria a lo que sucedía en Alejandría en ese mismo momento en donde los objetos si proyectaban sombra. Eratóstenes midió el tamaño de la Tierra utilizando funciones trigonométricas, midiendo el ángulo con el que incidían los rayos solares sobre Alejandría en el mediodía solar del solsticio de verano y conociendo la distancia entre Alejandría y Siena. Actualmente la trigonometría también se utiliza para medir la distancia a estrellas cercanas por medio del método de “paralaje estelar”.

Las funciones seno y coseno tienen una peculiaridad, y es que poseen comportamiento periódico, es decir, sus valores se repiten con cierta frecuencia a lo largo de todo el eje de los números reales. Esta característica de las funciones seno y coseno las hace candidatas perfectas para modelar fenómenos que tengan comportamientos oscilatorios como las ondas, el movimiento circular, los movimientos planetarios, los circuitos de corriente alterna, etc.

Además, la trigonometría juega un papel fundamental en la construcción y en el análisis de señales. Cualquier señal periódica puede descomponerse como una suma de funciones trigonométricas, y viceversa. De esta manera la trigonometría nos ayuda a entender señales de todo tipo, desde aquellas utilizadas en comunicaciones hasta las generadas por procesos electrofisiológicos en nuestro cuerpo.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Art. actualizado: Julio 2023; sobre el original de enero, 2009.

Datos para citar en modelo APA: Zamora Ramírez, A. (Julio 2023). Definición de Trigonometría. Significado.com. Desde https://significado.com/trigonometria/