Significado de centro de masa Definición, distribución, y ejemplos

Licenciada en Física
Definición formal
El centro de masa de un sistema de partículas, o directamente, el de un cuerpo extenso, determinando el punto en el que se centra la masa. Allí se aplica la fuerza resultante, de manera que el movimiento global del cuerpo, aún si es complejo, se describe fácilmente mediante el del centro de masas.
Para visualizar esto, considérese un objeto proyectado oblicuamente. Bajo la acción de la gravedad, el movimiento del objeto es parabólico, ya que su centro de masas describe una parábola. Sin embargo, al observar cuidadosamente otros puntos del cuerpo, se ve que llevan a cabo movimientos complejos de rotación, a medida que el centro de masas va siguiendo la parábola.
Está claro que es mucho más fácil analizar el movimiento global del objeto a través de un único punto, que describir todos y cada uno de los movimientos individuales de las partículas que componen el cuerpo.
Sobre el centro de masa de un cuerpo se aplican fuerzas que pueden tratarse con las leyes de Newton sin mayor problema.
Cómo calcular el centro de masas
Si se tienen dos partículas idénticas, de masa m cada una, intuitivamente se sabe que el centro de masas del sistema está en la mitad de la línea que las une. En cambio, si las partículas son distintas, el centro de masas aún sigue sobre la línea de unión, pero más cerca de la más pesada.
Al tratarse de un objeto extendido simétrico, el centro de masas se encuentra en algún punto del eje de simetría. Por ejemplo, en un disco homogéneo, el centro de masa coincide con el centro geométrico.
Pero no tiene que existir masa en el centro de masas. En un donut, el centro de masas coincide con el centro geométrico, pero no hay masa allí.
En cuanto a la forma de calcular la ubicación, se distinguen dos casos, el primero es el de un conjunto de partículas dispersas, y el segundo, el de un objeto extendido. El primer caso corresponde a una distribución discreta de masas y el segundo, a una distribución continua.
Centro de masas de la distribución discreta
Para establecer la posición del centro de masa de un sistema de N partículas, se dispone de un sistema de referencia, para ver cuál es la posición de cada una. Este es un vector llamado \(\vec{r}\), que depende de las coordenadas espaciales x, y, z.
Sea \({{\vec{r}}_{1}}\) la posición de la partícula 1, cuya masa es \({{m}_{1}}\), \({{\vec{r}}_{2}}\) la posición de la partícula de masa \({{m}_{2}}\) y así sucesivamente, hasta llegar a la partícula N-ésima, de posición \({{\vec{r}}_{N}}\) y masa \({{m}_{N}}\).
La localización del centro de masas del conjunto, denotado CM, se calcula a través de la siguiente ecuación:
\({{\vec{r}}_{{CM}}}=\frac{{{{m}_{1}}{{{\vec{r}}}_{1}}+{{m}_{2}}{{{\vec{r}}}_{2}}+{{m}_{3}}{{{\vec{r}}}_{3}}+\ldots +{{m}_{N}}{{{\vec{r}}}_{N}}}}{{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}\ldots +{{m}_{i}}}}\)
Es una ecuación vectorial que se desglosa en tres ecuaciones, una para cada componente del vector de posición en el espacio. Si el sistema está en el plano basta con dos ecuaciones, y si se trata de partículas localizadas sobre un mismo eje, solo se necesita una ecuación.
Al usar el símbolo de sumatoria, la ecuación queda más compacta:
\({{\vec{r}}_{{CM}}}=\underset{{i=1}}{\overset{N}{\mathop \sum }}\,\frac{{{{m}_{i}}{{{\vec{r}}}_{i}}}}{{{{m}_{i}}}}=\frac{1}{M}\underset{{i=1}}{\overset{N}{\mathop \sum }}\,{{m}_{i}}{{\vec{r}}_{i}}\)
El denominador de la expresión es la sumatoria de todas las masas de las N partículas que participan del sistema. Esta es su masa total M.
Centro de masas de la distribución continua
Si las partículas que componen el sistema son minúsculas y no se distinguen, se trata de un objeto extenso, y hay que sustituir la sumatoria por una integral, que se efectúa sobre todo el volumen V del objeto:
\({{\vec{r}}_{{CM}}}=\frac{1}{M}\underset{V}{\overset{{}}{\mathop \int }}\,\vec{r}dm\)
En esta expresión, dm es una masa infinitesimal, es decir, un diferencial de masa, y \(\vec{r}\) es una función vectorial de las coordenadas x, y, z.
Ejemplo de cálculo
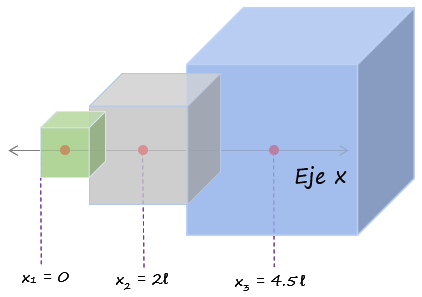
Los tres cubos de la figura están hechos del mismo material homogéneo. El más pequeño tiene lado ℓ, el del medio 2ℓ y el más grande 3ℓ. Los centros de cada cubo están alineados. ¿Dónde está ubicado el centro de masas del sistema?
Respuesta
En primer lugar, se necesita conocer la masa de cada cubo. Si los tres son del mismo material, cuya densidad es ρ, la masa de cada uno es el producto de la densidad por el volumen:
m = ρ · V
Ahora bien, el volumen de un cubo es su lado elevado al cubo. Los cubos se distinguirán así: m1 es el más pequeño, m2 el mediano y m3 el mayor. Sus respectivos lados son ℓ, 2ℓ y 3ℓ, de manera que:
\({{m}_{1}}=\rho {{\ell }^{3}}\)
\({{m}_{2}}=\rho {{\left( {2\ell } \right)}^{3}}=8\rho {{\ell }^{3}}\)
\({{m}_{3}}=\rho {{\left( {3\ell } \right)}^{3}}=27\rho {{\ell }^{3}}\)
El centro de masas de cada cubo está localizado en su centro geométrico. Se tratará a cada cubo como si fuera una partícula, cuya masa está en el centro de masas respectivo.
El siguiente paso es establecer un sistema de coordenadas con un origen. Como la figura compuesta tiene como eje de simetría al eje x, ya se sabe que el CM estará ubicado en algún lugar allí.
En cuanto al origen, se puede elegir en el borde izquierdo del cubo más pequeño. Esta elección es arbitraria, ya que se puede escoger cualquier otro punto sobre el eje x, en todo caso, el CM no depende del sistema de referencia.
Con esta elección, la posición del CM de cada cubo es:
\({{x}_{1}}=0.5\ell \)
\({{x}_{2}}=2\ell \)
\({{x}_{3}}=4.5\ell \)
Ahora se sustituye todo esto en la ecuación para el CM de la distribución discreta. Dado que el CM está sobre el eje x, se puede prescindir de la notación vectorial:
\({{x}_{{CM}}}=\frac{{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}}}{{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}}=\frac{{\left( {\rho {{\ell }^{3}}\times 0.5\ell } \right)+\left( {8\rho {{\ell }^{3}}\times 2\ell } \right)+\left( {27\rho {{\ell }^{3}}\times 4.5\ell } \right)}}{{\rho {{\ell }^{3}}+8\rho {{\ell }^{3}}+27\rho {{\ell }^{3}}}}=\frac{{138\ell }}{{36}}=\frac{{23\ell }}{6}\)
\({{x}_{{CM}}}=3.83\ell \)
El CM está ubicado a 3.83ℓ, contando desde el borde izquierdo del cubo pequeño. Esto significa que el CM se encuentra en el cubo más grande, un poco a la izquierda del centro de este. Tiene sentido, pues el CM está más cerca de la partícula con mayor masa.

Trabajo publicado en: Ene., 2022.