Significado de teorema de Steiner Definición, y ejemplos

Licenciada en Física
Definición formal
El Teorema de Steiner, practicado ampliamente en mecánica, relaciona el momento de inercia I de un cuerpo alrededor de cierto eje z, con el momento de inercia ICM respecto a un eje distinto z’, paralelo al primero y que pasa por su centro de masas. Asimismo, esta formulación es referida como ejes paralelos.
Según el teorema, la relación entre los dos momentos de inercia es
\(I={{I}_{CM}}+M{{d}^{2}}\)
Donde, M es la masa del objeto, y d es la distancia entre los ejes.
La siguiente figura ilustra el teorema y la geometría del mismo sobre un objeto de forma arbitraria, cuyo centro de masa CM es el punto de color rojo:
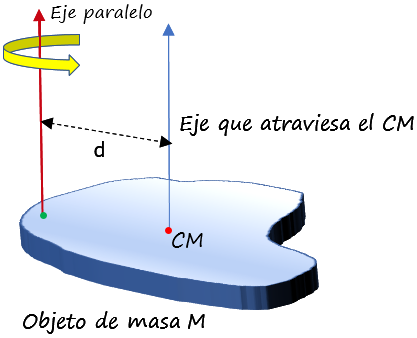
El momento de inercia en torno a un eje es una cualidad importante de los cuerpos sólidos, ya que entre mayor sea su valor, más energía se requiere para cambiar la velocidad de rotación de dicho cuerpo.
En la práctica, no es difícil comprobar que algunos objetos se ponen a girar con más facilidad respecto a un eje que respecto a otro. Por ejemplo, es más sencillo hacer girar un disco alrededor de un eje de simetría que pasa por su centro, que sobre un eje que pase por el borde.
En los objetos homogéneos y simétricos, los ejes de simetría coinciden con los ejes principales de rotación.
Uso aplicado del teorema
En principio, los objetos tienen infinitos momentos de inercia, ya que a su vez existen infinitos ejes alrededor de los cuales rotar. Normalmente, los momentos de inercia respecto a los ejes principales son los que aparecen tabulados, así que cuando se tiene un objeto girando alrededor de un eje que no atraviesa el centro de masas, habría que llevar a cabo el cálculo del momento de inercia mediante su definición, que normalmente involucra el cálculo de integrales.
El teorema de Steiner ahorra el trabajo de cálculo, siempre que el eje arbitrario de rotación sea paralelo a uno que atraviese el CM.
En ese caso, basta con buscar en una tabla el valor de ICM, y sumarle el producto entre la distancia que separa los ejes, elevada al cuadrado y la masa del objeto. Así se obtiene rápidamente el momento de inercia respecto al eje deseado sin tener que integrar.
Nótese que, de la ecuación I=ICM + Md2 , se deduce lo siguiente:
El momento de inercia I, calculado respecto a un eje paralelo que no pasa por el centro de masa del objeto, siempre es mayor que ICM, ya que la cantidad Md2 es positiva.
Ejemplos que ilustran la aplicación del teorema
Momento de inercia en un aro de masa M y radio R en un eje que pasa por su borde
El primer paso es hallar en las tablas el momento de inercia del aro delgado de radio R y masa M, sobre un eje que pase por el centro de masas, encontrando:
\({{I}_{CM}}=M{{R}^{2}}\)
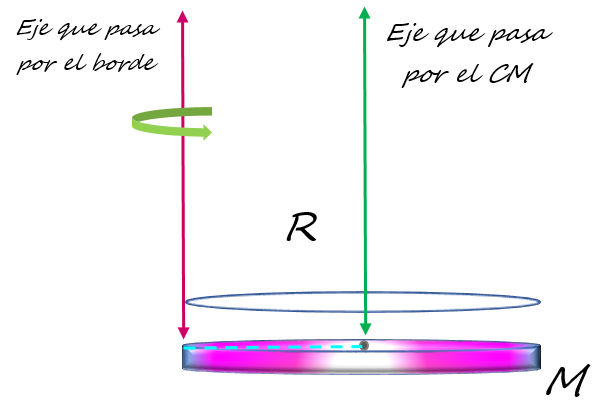
El segundo paso es determinar la distancia entre los ejes. Como el centro de masas del aro coincide con el centro geométrico, el eje que pasa por el CM y el que pasa por el borde están separados una distancia d = R.
Sustituyendo la ecuación anterior y los datos del problema (M y d=R) en el teorema de Steiner, se obtiene:
\(I={{I}_{CM}}+M{{d}^{2}}=M{{R}^{2}}+M{{R}^{2}}=2M{{R}^{2}}\)
Momento de inercia en una lámina cuadrada uniforme en un eje que pasa por la esquina
La medida del lado de la lámina cuadrada es ℓ y su masa es M. En una tabla, el momento de inercia referido al centro de masas del cuadrado es:
\({{I}_{CM}}=\frac{1}{12}M{{\ell }^{2}}\)
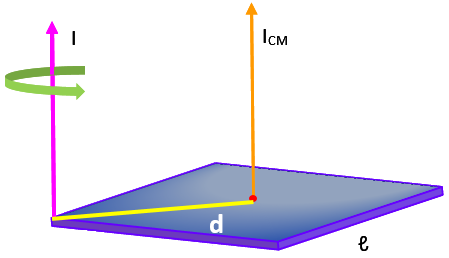
Para calcular el momento de inercia respecto al eje que pasa por la esquina, es preciso hallar la distancia “d”, entre este punto y el centro de masas, que está en el centro geométrico.
En el cuadrado visto desde arriba, se ve que es necesario hallar la diagonal del cuadrado con el teorema de Pitágoras, ya que la distancia entre los ejes es, precisamente, la mitad de la diagonal.

\(2d=\sqrt{{{\ell }^{2}}+{{\ell }^{2}}}\)
\(2d=\sqrt{2{{\ell }^{2}}}\)
Por lo tanto
\(d=\frac{\sqrt{2{{\ell }^{2}}}}{2}=\frac{\sqrt{2}}{2~}\ell \)
Ahora se sustituyen 1) y 2) en el teorema de Steiner para encontrar el momento de inercia I respecto al eje que pasa por la esquina
\(I={{I}_{CM}}+M{{d}^{2}}\)
\(I=\frac{1}{12}M{{\ell }^{2}}+M{{\left( \frac{\sqrt{2}}{2}\ell \right)}^{2}}\)
Con un poco de álgebra se llega a
\(I=\frac{1}{12}M{{\ell }^{2}}+M\left( \frac{2{{\ell }^{2}}}{4} \right)=\frac{7}{12}M{{\ell }^{2}}\)

Trabajo publicado en: May., 2021.