Significado de teorema del coseno Definición, demostración, y ejemplos

Licenciada en Física
Definición formal
El teorema del coseno es una operación a través de la cual conocer el valor de un lado de un triángulo, a partir de los datos numéricos que determinan los otros dos lados y el coseno del ángulo entre ellos.
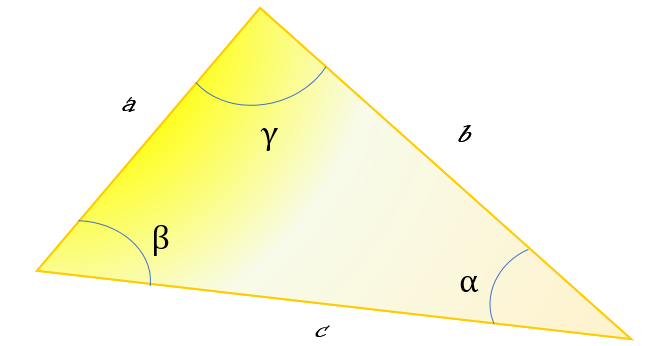
Por ejemplo, supóngase que se quiere conocer el lado “c” del triángulo mostrado en la figura arriba, teniendo la medida de los lados “a” y “b” y el ángulo entre ellos, que es γ. Matemáticamente, el procedimiento se resume en
c2 = a2 + b2 – 2ab ∙ cos γ
Traducido en palabras, expresa que el cuadrado de uno de los lados del triángulo es la suma de los cuadrados de los dos lados restantes, menos el doble producto entre estos lados y el coseno del ángulo que hay entre ellos.
Si el triángulo fuera rectángulo, con los lados “a” y “b” como sus catetos y el lado “c” la hipotenusa, el ángulo γ valdría 90º. Dado que el coseno de 90º es igual a 0, el teorema del coseno se reduciría en este caso al teorema de Pitágoras, que es válido únicamente para los triángulos rectángulos:
c2 = a2 + b2
En cambio, el teorema del coseno es funcional a todos los triángulos, y abarca al teorema de Pitágoras como un caso particular.
El teorema del coseno puede plantearse para los otros lados del triángulo, en tal caso se pueden escribir las siguientes expresiones:
a2 = b2 + c2 – 2bc ∙ cos α
b2 = a2 +c2 -2ac ∙ cos β
La primera vez que el teorema se menciona, que se sepa, es en los Elementos de Euclides (siglo III a.C.), aunque allí aparece con una formulación un tanto diferente de la que se usa actualmente, porque en ese entonces todavía no se conocían las razones trigonométricas como el coseno. Estas vendrían tiempo después, de la mano de los matemáticos árabes.
Demostración
Existen varias maneras de demostrar el teorema del coseno, en el ejemplo que analizamos, se trabaja con el teorema de Pitágoras.
En la siguiente figura trazamos la altura “h” en rojo, dividiendo el triángulo en dos triángulos rectángulos.
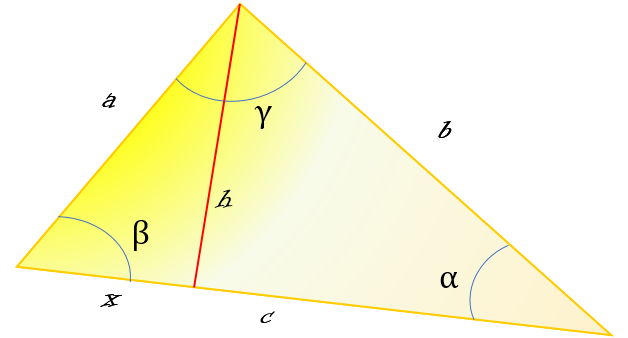
El triángulo rectángulo de la izquierda tiene catetos “h” y “x”, mientras que su hipotenusa es “a”. Siendo un triángulo rectángulo, es válido aplicar el teorema de Pitágoras y afirmar que
1) \({{a}^{2}}=~{{x}^{2}}+{{h}^{2}}\)
En el otro triángulo rectángulo, los catetos son “h” y “c−x”, mientras que la hipotenusa es “b”. Para él se afirma esta otra expresión
2) \({{b}^{2}}=~{{\left( c-x \right)}^{2}}+{{h}^{2}}\)
Ahora se despeja h2 de la ecuación 1) y queda
3) \({{h}^{2}}={{a}^{2}}-{{x}^{2}}\)
Y el despeje se sustituye en 2)
4) \({{b}^{2}}=~{{\left( c-x \right)}^{2}}+{{a}^{2}}-{{x}^{2}}\)
A continuación se desarrolla el producto notable y se simplifican términos
5) \({{b}^{2}}=~{{c}^{2}}-2cx+{{x}^{2}}+{{a}^{2}}-{{x}^{2}}={{a}^{2}}+{{c}^{2}}-2cx\)
El ángulo que hay entre “a” y “c” es β, cuyo coseno es
6) \(cos\beta =\frac{x}{a}\)
Despejando “x” de 6)
7) \(x = a ∙ cos β\)
Llevando el resultado 7) a la expresión 5) queda
8) b2 = c2 – 2cx+x2 + a2 – x2 =a2 + c2 – 2ac ∙ cos β
Esta igualdad es precisamente el teorema del coseno para calcular el valor del lado “b”. Siguiendo esta misma metodología se hace la demostración respectiva para los lados “a” y “c”, análogas a la que se muestra aquí.
Ejemplos prácticos
Ejemplo resuelto 1
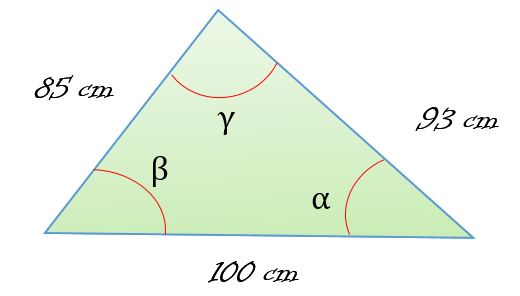
Las medidas de los lados de un triángulo son las siguientes:
• a= 93 cm
• b= 85 cm
• c= 100 cm
¿Cuánto miden sus ángulos internos?
Respuesta
De cualquiera de las expresiones para el teorema del coseno se despeja el coseno del ángulo correspondiente:
\(c^{2} = a^{2} + b^{2} – 2ab ∙ cos γ\)
\(\cos \gamma =\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}\)
Se sustituyen los valores dados en el enunciado
\(arc\cos 0.371537=68.2{}^\text{o}\)
De
Se despeja cos α
\(\cos \alpha =\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\)
\(\cos \alpha =\frac{{{85}^{2}}+{{100}^{2}}-{{93}^{2}}}{2∙85∙100} = 0.5044706\)
\(arc cos 0.5044706=59.7º\)
Dado que
\(\alpha +\beta +\gamma =180{}^\text{o}\)
Se deduce que
\(\beta =180{}^\text{o}-\alpha -\beta =180{}^\text{o}-59.7{}^\text{o}-68.2{}^\text{o}=52.1{}^\text{o}\)
También podía despejarse su valor de la tercera relación del teorema del coseno
\(\cos \beta =\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}\)
\(\cos \beta =\frac{{{93}^{2}}+{{100}^{2}}-{{85}^{2}}}{2∙93∙100}=0.61419355\)
\(arc cos 0.61419355 = 52.1º\)
Ejemplo resuelto 2
Un espectador mira la pantalla de un cine con ángulo de 26.5º. Si se encuentra a 31 m de uno de los extremos de la pantalla y a 33 m del otro, ¿cuál es el ancho de la pantalla?
Respuesta
Visto desde arriba, el triángulo es el siguiente:
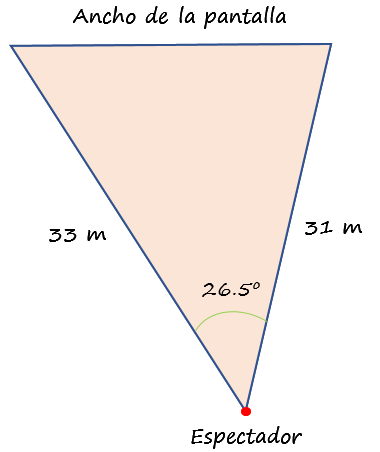
Sea “d” el ancho de la pantalla, como se conocen dos de los lados del triángulo y el ángulo entre ellos, el teorema del coseno quedaría así:
d= √(〖31〗^2+〖33〗^2-2∙31∙33∙cos〖26.5º〗 )= √(218.96 ) m=14.8 m
La pantalla tiene un ancho de 14.8 m.

Trabajo publicado en: Abr., 2021.