Significado de teorema de Pitágoras Definición, comprobación, y funciones

Licenciada en Física
Definición formal
El teorema de Pitágoras Expresa la relación existente entre los lados de un triángulo rectángulo, es decir, aquel triángulo que tiene un ángulo interno de 90º (ángulo recto). Los lados que conforman el ángulo recto se denominan catetos, y el lado restante es la hipotenusa. El teorema establece que la sumatoria de los cuadrados de los catetos equivale al cuadrado de la hipotenusa.
El enunciado del teorema de Pitágoras se representa matemáticamente a través de
\(c^2 = a^2 + b^2\)
A continuación se muestra un triángulo rectángulo, cuyos catetos son a y b, y la hipotenusa es c.
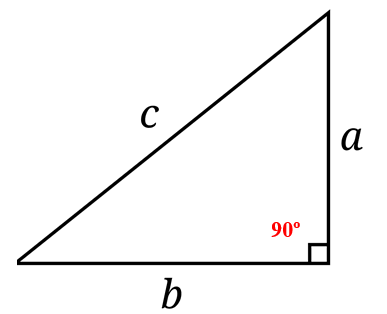
Si se quiere conocer la longitud de la hipotenusa, simplemente se toma la raíz cuadrada positiva a ambos lados de la igualdad:
\(c=\sqrt{{{a}^{2}}+{{b}^{2}}}\)
Asimismo, si se conocen la hipotenusa y uno de los catetos, es posible hallar el valor del cateto restante mediante despeje directo:
\(a=\sqrt{{{c}^{2}}-{{b}^{2}}}\)
\(b=\sqrt{{{c}^{2}}-{{a}^{2}}}\)
El descubrimiento se atribuye al famoso matemático griego de la antigüedad Pitágoras de Samos (569-475 a.C.), aunque algunos historiadores aseguran que el teorema ya era conocido por los matemáticos chinos desde hacía tiempo, si bien Pitágoras probablemente jamás tuvo contacto con ellos o sus tratados, de modo que lo definió de manera independiente.
Pitágoras de Samos fue también un filósofo, músico y pensador notable, creador de la escuela pitagórica, una institución de naturaleza dual: científica y religiosa, que influyó en muchos otros pensadores que le siguieron, como Platón y Aristóteles.
Comprobación del teorema
Se puede demostrar de muchas formas, tanto algebraicas como geométricas. Seguidamente se propone una forma de demostrar la relación entre los lados del triángulo, partiendo de cuadrados, triángulos y álgebra elemental.
Un cuadrado es una figura geométrica plana de cuatro lados iguales, cuya área se calcula elevando al cuadrado la longitud del lado.
Inicialmente se dibuja un cuadrado azul al que se añade otro cuadrado blanco más pequeño en su interior, de lado c. Las cuatro regiones que se forman a los lados son triangulares e idénticas, de catetos a y b.
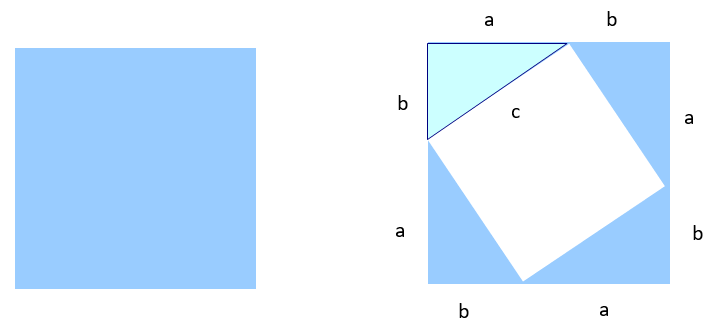
El área del cuadrado blanco es \({{c}^{2}} \), el área del triángulo verde es 1/2 a∙b, pero los restantes 3 triángulos son idénticos, por lo tanto el área triangular completa es 4(1/2 a∙b) = 2ab. Por su parte, el área del cuadrado azul original, el de la izquierda, es \({{\left( a+b \right)}^{2}}\), pero esta equivale a la suma de las dos primeras áreas.
Entonces:
\({{\left( a+b \right)}^{2}}=\text{ }{{c}^{2}}+\text{ }2ab\)
Al desarrollar el producto notable del lado izquierdo queda:
\({{a}^{2}}+\text{ }2ab\text{ }+\text{ }{{b}^{2}}=\text{ }{{c}^{2}}+\text{ }2ab\)
El término 2ab se cancela por estar presente a ambos lados de la igualdad con el mismo signo, por lo tanto, la expresión se simplifica a:
\({{a}^{2}}~+\text{ }{{b}^{2}}=\text{ }{{c}^{2}}\)
Que es precisamente el teorema de Pitágoras.
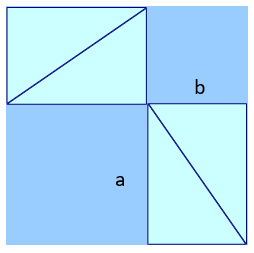
Otra manera de verlo es reacomodando los cuatro triángulos como se muestra en la figura de abajo. Quedan dos cuadrados azules de diferente área: \({{a}^{2}} \) y \({{b}^{2}} \), la suma de estas áreas es igual a la del cuadrado blanco en el dibujo de arriba, que es \({{c}^{2}} \). La igualdad conduce de nuevo al teorema de Pitágoras:
\({{a}^{2}}~+\text{ }{{b}^{2}}=\text{ }{{c}^{2}}\)
Funciones de aplicación del teorema de Pitágoras
Siempre que se forme un triángulo rectángulo, el teorema de Pitágoras sirve para encontrar uno de los lados, conocidos los otros dos, por lo que es de mucha utilidad para encontrar longitudes desconocidas. Lo bueno es que entre los objetos cotidianos esta forma triangular es frecuente, y también en diversas áreas de la Física y la Matemática. Por eso el teorema puede usarse para:
– Encontrar velocidad con que se lanza un proyectil formando un ángulo θ con la horizontal, si se conocen las componentes cartesianas de la velocidad.
– Determinar la magnitud de la fuerza resultante al sumar vectorialmente dos fuerzas perpendiculares.
– Calcular distancias y áreas desconocidas en figuras geométricas en las que participan triángulos rectángulos.
– Representar gráficamente números irracionales, así como números complejos en el plano complejo.
– Saber si un triángulo es o no es rectángulo.
– Calcular la impedancia de un circuito RLC serie.
Ejercicio práctico e ilustrativo
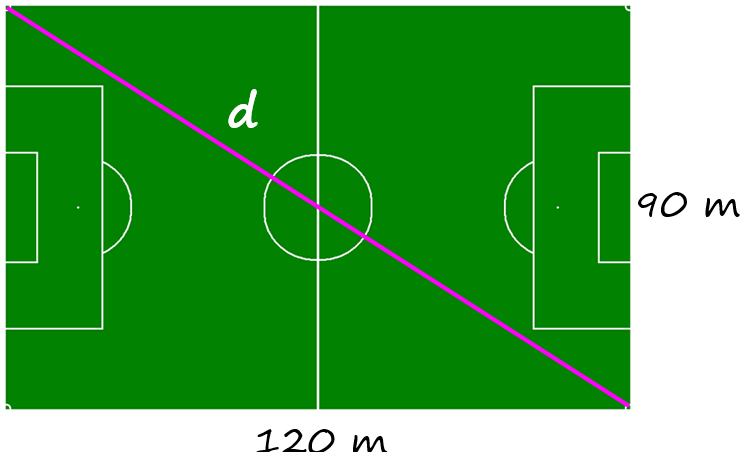
Como parte de su rutina diaria de entrenamiento, un atleta corre de ida y vuelta varias veces sobre la diagonal de un campo de fútbol, cuyas medidas son 120m x 90m. Si el atleta recorre la diagonal 25 veces, ¿qué distancia total recorrió?
Respuesta
La diagonal d del terreno corresponde a la hipotenusa de un triángulo rectángulo de catetos 120m y 90m, por lo tanto:
\(d=\sqrt{{{120}^{2}}+{{90}^{2}}}m=150m\)
Como el atleta recorre la diagonal 25 veces durante su entrenamiento, la distancia total recorrida D es igual a:
D = 25 x 150m = 3750m

Trabajo publicado en: Nov., 2020.