Significado de derivada Definición, propiedades, y funciones no derivables

Doctor en Ingeniería
Definición formal
La derivada de una función de valores reales es una cuantificación de la rapidez con que cambia el valor de la función conforme cambia el valor de la variable.
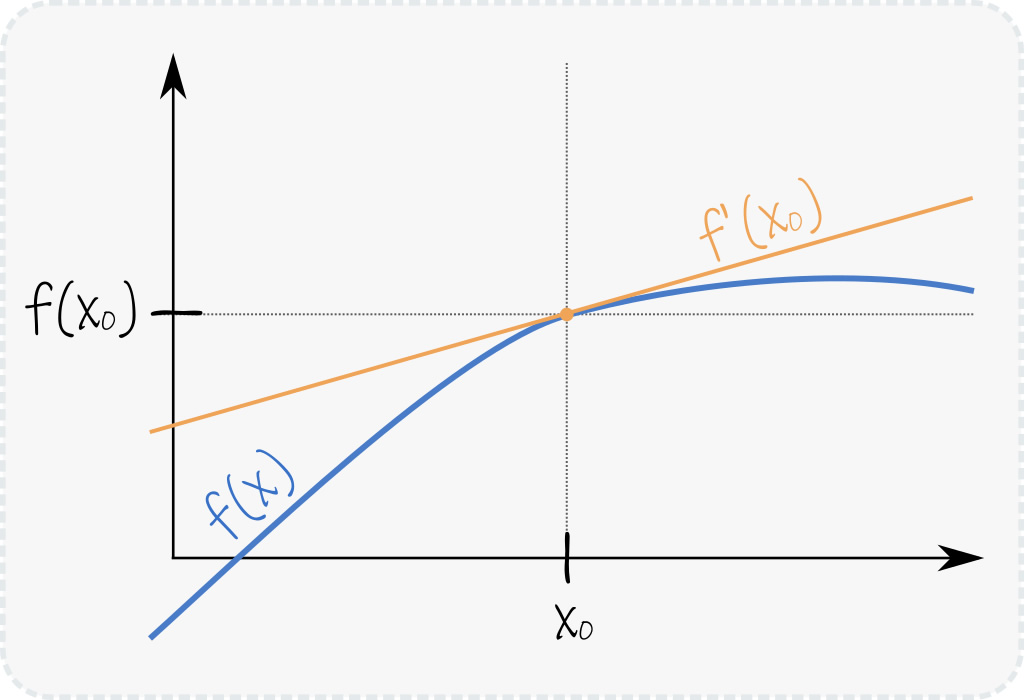
En otras palabras, si \(f:\mathbb{R}\rightarrow \mathbb{R}\) es derivable en un punto x0, su derivada f'(x0) es la pendiente de la recta tangente a la curva en (x0, f(x0)) .
La derivada de f(x) en x0 se define formalmente como
\(f'(x_0) \doteq \lim_{h\rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h}, \quad h\in \mathbb{R}\)
La expresión dentro del límite se conoce como cociente incremental y da cuenta de cuánto cambia el valor de f(x) en función de un cambio de abscisas h. Esto quiere decir que
\(f(x_0+h) \approx f(x_0) + f'(x_0)h\) ,
por lo que conocer la derivada de una función en un punto nos permite conocer de manera aproximada el valor de la función alrededor de ese punto. Esta aproximación es lineal como función de h, por lo que resulta muy útil en muchas aplicaciones donde calcular f(x) de manera exacta requiere mucho poder de cómputo.
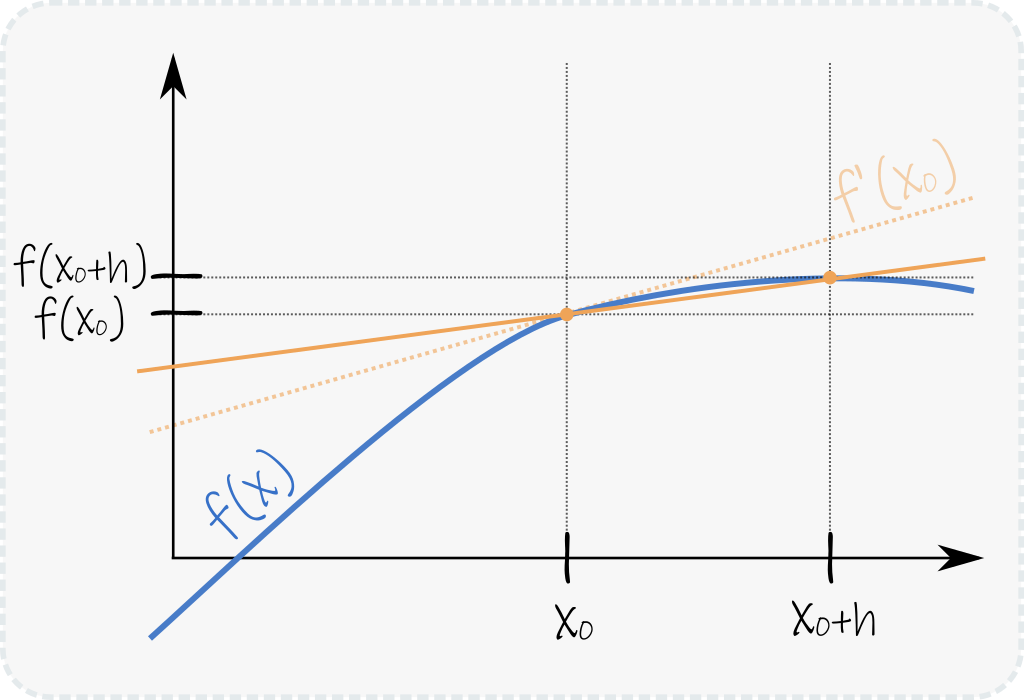
Notar que a medida que h decrece, el punto de la derecha que determina la recta secante en la Figura 2 se acerca a (x0, f(x0)) y la secante se acerca a la tangente con pendiente f'(x0).
Propiedades identificables en una derivada
La derivada tiene varias propiedades interesantes, de las que se desprenden muchas aplicaciones. Las más importantes quizás sean las siguientes:
– Toda función derivable es continua.
– Si f y g son funciones derivables, entonces \((f(x)+g(x))’ = f'(x)+g'(x)\)
– Si f es derivable y \(k\in\mathbb{R}\) , entonces \((kf(x))’ = kf'(x)\) .
– Regla del producto: Si f y g son funciones derivables, entonces \((f(x)g(x))’ = f'(x)g(x)+f(x)g'(x)\)
– Regla del cociente: Si f y g son derivables y \(g(x)\neq 0\), entonces \(\left(\frac{f(x)}{g(x)}\right)’ = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\) .
– Regla de la cadena: \((\,f(\,g(x)\,)\,)’= f'(g(x))g'(x)\) .
– Teorema Fundamental del Cálculo: Si F es una primitiva de f, entonces \(F'(x) = f(x)\).
Estas propiedades son muy utilizadas para realizar cálculos y desarrollar modelos en un sinfín de aplicaciones, además de la demostración de teoremas.
Es oportuno mencionar que la derivación tiene su homólogo en múltiples dimensiones, denominado diferenciación, que está basada en la misma noción de aproximar una función en un punto a través de una transformación lineal. Supongamos que \(f:\mathbb{R}^M\rightarrow\mathbb{R}^N\) . Entonces, decimos que f es diferenciable en x0 si existe una transformación lineal \(J[x_0]:\mathbb{R}^M\rightarrow\mathbb{R}^N\) tal que
\(\lim_{\|h\|\rightarrow 0} \frac{\|f(x_0+h)-f(x_0)-J[x_0](h)\|}{\|h\|} = 0\)
Esto, de nuevo, quiere decir que la transformación lineal J[x0] (llamada Jacobiano) aproxima a la función f en un entorno de x0. La diferenciación tiene propiedades muy similares a la derivación, que no son otra cosa que generalizaciones al cálculo multivariado.
Derivabilidad: funciones no derivables
No todas las funciones son derivables. Dado que hemos dicho que la derivada de una función en un punto es la pendiente de la recta tangente que pasa por ese punto, entonces la curva debe, primero, admitir una tangente en ese punto.
Formalmente, diremos que f es derivable en x0 si y sólo si existe f'(x0) que cumple
\(\lim_{h\rightarrow 0} \frac{|f(x_0+h)-f(x_0)-f'(x_0)h|}{|h|} = 0\)
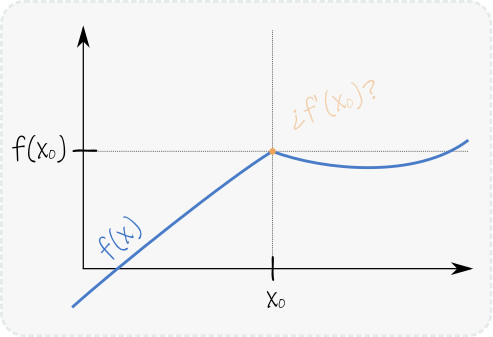
Intuitivamente, podemos pensar que para que una función sea derivable en un punto, debe ser suave y sin discontinuidades. Es decir, no debe ocurrir lo que se observa en la Figura 3. Lo que ocurre es que
\(\lim_{h\rightarrow 0^-} \frac{f(x_0+h)-f(x_0)}{h} \neq \lim_{h\rightarrow 0^+} \frac{f(x_0+h)-f(x_0)}{h}\) ,
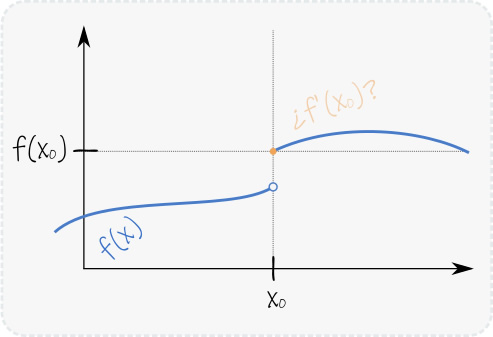
es decir, que el el límite del cociente incremental es distinto por izquierda (si h es negativo) que por derecha (si h es positivo), por lo que no se cumple la definición. Por otra parte, en el ejemplo de la derecha, la función tiene una discontinuidad en x0, y por lo tanto no se cumple la condición necesaria de continuidad para derivabilidad que veremos a continuación.

Trabajo publicado en: Feb., 2021.