Significado de integrales Definición, explicación, y función primitiva

Doctor en Ingeniería
Definición formal
Integrales es el valor numérico que se le asigna a una función para cuantificar el área (o volumen, o medida análoga) comprendida entre la función y un subconjunto de su dominio, y cuya definición matemática formal, que analizamos en este texto, es tan elegante y precisa como inútil cuando lo encontramos por primera vez.
Para ilustrarlo de forma didáctica, supongamos que queremos pintar una pared y tenemos que comprar la pintura. Si la pared es rectangular, entonces es fácil: multiplicamos la medida de la base por la altura y obtenemos el área, pero ¿qué pasa cuando el techo está inclinado o tiene un arco y por lo tanto la pared es irregular? Si conociéramos la función que describe el borde entre la pared y el techo, podríamos calcular el área bajo la curva (ver Figura 1), y aunque su uso es principalmente otro que la pinturería, esto describe el concepto de integración.
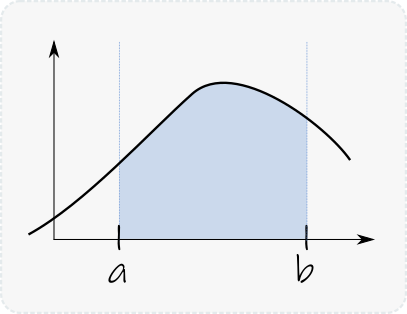
La integral explicada de acuerdo a su definición formal
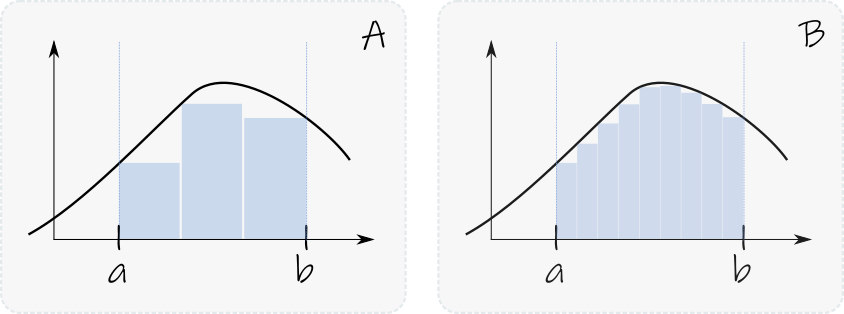
Reconociendo su objetivo, que consiste en calcular el área bajo una curva, ¿cómo lo hacemos? Si sabemos calcular el área de un rectángulo, podemos aprovecharlo. Si llenamos de rectángulos el espacio bajo la curva, como se ve en la Figura 2A, y sumamos las áreas, entonces podemos tener una idea aproximada del área de la curva. Esta aproximación puede parecer mala, ¡y lo es! Pero puede mejorarse si utilizamos rectángulos más chicos, como en la Figura 2B, donde se ve que queda menos área sin cubrir. La idea detrás de la definición formal de integral es entonces generar una partición con rectángulos cada vez más chicos y tomar el límite de esa área a medida que la partición se hace más fina.
Consideremos entonces una función \(f:\mathbb{R}\rightarrow \mathbb{R}\) y un intervalo no vacío [a, b] y una partición \(P_\delta\doteq \{[x_0,x_1],[x_1,x_2], \ldots [x_{N-1},x_N]\}\), donde \(x_0 = a\), \(x_N = b\) y Δ es la longitud del intervalo más grande. Entonces, la suma de las áreas de los rectángulos en la Figura 3L puede escribirse como
\(
\begin{align*}
L(f;P_\delta) = \sum_{n=0}^{N-1} m_n(x_{n+1}-x_n), & \quad\quad m_n = \inf_{x_n\leq x\leq x_{n+1}} f(x).
\end{align*}
\)
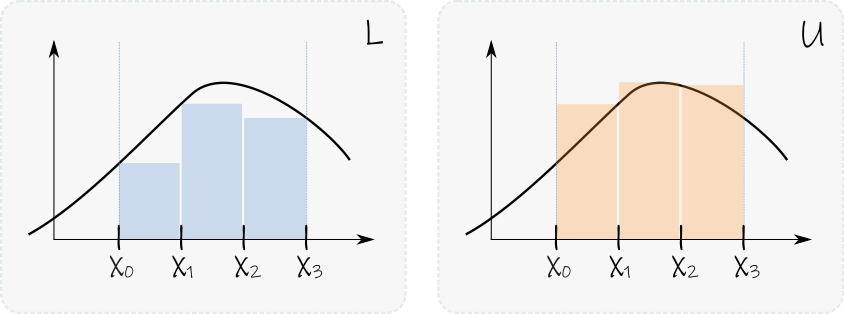
De manera análoga, si nos «pasamos con la pintura», podemos definir nuestros rectángulos de forma que aproximen a nuestra función por encima, como en la Figura 3U. Definimos así la suma superior
\(
\begin{align*}
U(f;P_\delta) = \sum_{n=0}^{N-1} M_n(x_{n+1}-x_n), & \quad\quad M_n = \sup_{x_n\leq x\leq x_{n+1}} f(x).
\end{align*}
\)
La integral (de Riemann) de f en [a,b] se define formalmente entonces como \(\int_a^b f(x)dx = S\) si -y sólo sí-
\(
\begin{align*}
\lim_{\delta \rightarrow 0} U(f;P_\delta) = S = \lim_{\delta \rightarrow 0} L(f;P_\delta).
\end{align*}
\)
Es decir, que una función es integrable en un subconjunto de su dominio si las sumas superiores \(U(f;P_\delta)\) y las sumas inferiores \(L(f;P_\delta)\) convergen al mismo número a medida que la partición \(P_\delta\) se afina. Esta no es la única manera de definir una integral, pero es quizás la más intuitiva. Cabe destacar que la noción de integral es extensiva a funciones con dominios más intrincados que \(\mathbb{R}\), pero la idea básica se mantiene.
Función primitiva para calcular la integral
En la práctica no vamos a ponernos a calcular el límite de las sumas de las áreas de los rectángulos cada vez que necesitemos conocer una integral, tal como lo expone su definición formal. Por lo tanto, para hacer esto más fácil, podemos introducir el concepto de función primitiva, denotada a menudo como \(\int f(x)\) o \(F(x)\). Una función primitiva (también llamada \emph{antiderivada}) cumple la propiedad:
\(
\begin{align*}
\int_a^b f(x) dx = F(b)-F(a), \quad\forall\; a,b \in\mathbb{R}.
\end{align*}
\)
Es decir, que si conocemos la primitiva de una función, podemos calcular su integral, y afortunadamente muchas de las funciones que usamos regularmente tienen una función primitiva. Por ejemplo, si f(x) = x, entonces \(F(x) = x^2/2+c\) (donde c es una constante), o si \(f(x) = cos(x)\), entonces \(F(x) = sin(x)+c\).
Finalmente, cabe mencionar la relación entre el concepto de función primitiva y derivada, que se conoce como Teorema Fundamental del Cálculo, que en pocas palabras establece que
\(
\begin{align*}
\frac{d}{dx} F(x) = f(x),
\end{align*}
\)
donde \(\frac{d}{dx}\) denota derivada con respecto a x. Esto quiere decir que integral y derivada son en algún sentido antagónicas, o bien que f(x) es la derivada de F(x) si -y sólo sí- F(x) es una primitiva de f(x).

Trabajo publicado en: Ene., 2021.