Significado de movimiento armónico simple Definición, características, y elementos

Licenciada en Física
Definición formal
El movimiento armónico simple es el movimiento repetitivo que sigue un móvil sobre una trayectoria fija y durante un intervalo de tiempo definido. Es periódico, y al tiempo T que le toma al móvil ejecutar un ciclo completo se le llama período. Ejemplos de movimientos que se pueden ajustar a este modelo son: I) el péndulo simple y II) el movimiento de vaivén que tiene una masa atada a un resorte vertical que se deja oscilar libremente.
Características del fenómeno
No todos los movimientos de vaivén son armónico simple, para que se le pueda considerar como tal, se identifica:
– La amplitud A de la magnitud que oscila, es decir, el desplazamiento máximo respecto a la posición de equilibrio, es constante.
– La fuerza que origina el movimiento, llamada fuerza de restitución, es directamente proporcional al desplazamiento “x” respecto a la posición de equilibrio.
– No se considera la fricción.
– El período del movimiento T tiene que ser independiente de la amplitud.
– La posición “x” en función del tiempo “t” y denotada como x(t), se describe mediante una función sinusoidal de la forma:
x(t) = A cos (ωt + φ)
Donde ω y φ son parámetros del movimiento, llamados respectivamente: i) frecuencia angular y ii) constante de fase. La gráfica de x(t) se muestra a continuación:
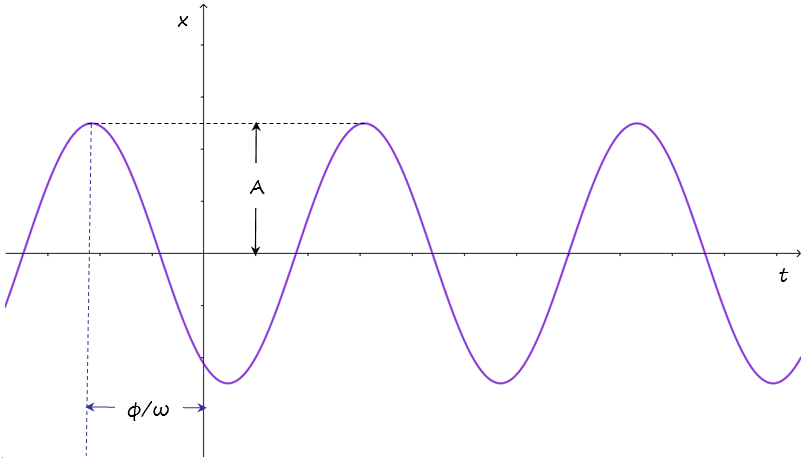
Elementos del MAS
– Período, es el tiempo que tarda en recorrer un ciclo completo, se denota como T y se mide en segundos (s).
– Fase de la vibración, corresponde al argumento del coseno: (ωt +φ) y se mide en radianes.
– Constante de fase, es el valor de la fase cuando t = 0 y también viene medida en radianes.
– Frecuencia, es una cantidad positiva que se denota como f y es el número de oscilaciones por unidad de tiempo. Sus unidades son de inverso de tiempo, es decir 1/s o s-1. Esta unidad recibe el nombre especial de hertz o hertzio y se abrevia Hz.
– Frecuencia angular, se denota con la letra griega ω y se define como el número de radianes por segundo.
– Amplitud, es el desplazamiento máximo de la magnitud que oscila, medido desde la posición de equilibrio. Si dicha magnitud es la posición, sus unidades son metros, si es velocidad son metros /segundo y si es aceleración son metros/segundo2.
Relación entre período, frecuencia angular y frecuencia
Como la función x(t) es periódica, significa que una vez que transcurre un ciclo en el tiempo T, la función vuelve a tener el valor que tenía en el tiempo t, en otras palabras:
x (t + T) = x (t)
Por las propiedades de las funciones senoidales, cuando la fase de la vibración aumenta en la cantidad 2π radianes, ocurre que:
[ω(t+T) + φ] – (ωt +φ) = 2 π
Por lo tanto hay una relación entre la frecuencia angular ω y el período T dada por:
ωT = 2 π
\(T=\frac{2\pi }{\omega }\)
Dado que la frecuencia f es el número de oscilaciones por unidad de tiempo, esto equivale al inverso del período:
\(f=\frac{1}{T}\)
Y la relación entre frecuencia f y frecuencia angular ω es:
\(f=\frac{\omega }{2\pi }\)
O bien
ω =2πf
Velocidad y aceleración en el MAS
Dado que la posición x(t) en el MAS está dada por:
x(t) = A cos (ωt + φ)
Y puesto que la velocidad es la primera derivada de la posición con respecto al tiempo:
\(\text{v(t)}=\frac{\text{dx}}{\text{dt}}=\frac{\text{d}}{\text{dt}}\left[ \text{Acos (}\omega \text{t}+\phi \text{)} \right]=-A\omega \cdot \text{s}en\text{ (}\omega \text{t}+\phi \text{)}\)
Nótese que como la velocidad depende de sen (ωt + φ) y la posición de cos (ωt + φ), ambas magnitudes están desfasadas en π/2. Por lo tanto el valor máximo de la velocidad ocurre cuando el móvil pasa por la posición de equilibrio y es:
vmax = Aω
En cambio, la velocidad es 0 cuando el móvil está en los puntos de retorno x = ± A.
Por su parte la aceleración es la derivada de la velocidad o la segunda derivada de la posición, respecto al tiempo:
\(\text{a(t)}=\frac{\text{dv}}{\text{dt}}=\frac{\text{d}}{\text{dt}}\left[ -A\omega \cdot \text{s}en\text{ (}\omega \text{t}+\phi \text{)} \right]=-\text{A}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}\cdot \text{cos (}\omega \text{t}+\phi \text{)}\)
Para la aceleración ocurre que su valor es cero en la posición de equilibrio y es máxima es los puntos de retorno. Este valor tiene magnitud de:
amax = Aω2
Como la aceleración tambien depende de cos (ωt + φ), es proporcional al desplazamiento, pero con sentido contrario, como indica el signo negativo.
Ejercicio
Una pieza de maquinaria tiene MAS de frecuencia f = 5.00 Hz y amplitud 1.80 cm. Calcular:
a) El tiempo que tarda en desplazarse desde x = 0 hasta x = −1.80 cm.
b) La velocidad máxima de la pieza.
Respuestas
a) El enunciado dice que A = 1.80 cm y f = 5.00 Hz.
Ahora bien, se tiene una oscilación completa cuando el móvil parte de x = 1.80 cm, pasa por x = 0 de ida, llega a x = −1.80 cm, vuelve a pasar por x = 0 de retorno y regresa a la posición original. Esto lo lleva a cabo en un tiempo t = T, que es el período del movimiento.
El período T y la frecuencia f están relacionados por:
\(T=\frac{1}{f}=\frac{1}{5Hz}=0.2s\)
El tiempo t buscado es el que se requiere para ir desde x = 0 hasta x = −1.80 cm, que es una cuarta parte del período. Entonces:
t = ¼ T = ¼ ∙0.2s = 0.05 s
b) La velocidad máxima es:
vmax = Aω
Y:
ω =2πf = 2π ∙5 s-1= 31.42 s-1
Por tanto:
vmax = 1.80 cm ∙ 31.42 s-1 = 56.55 cm/s

Trabajo publicado en: Ene., 2021.