Significado de ecuación de Dirac Definición, propiedades, y soluciones

Licenciada en Física
Definición formal
En su formulación original, la ecuación de Dirac describe el comportamiento de un electrón libre de interacciones, tomando en cuenta simultáneamente tanto los principios cuánticos como los relativistas. La ecuación de Dirac se puede escribir de varias formas, la que sigue es una muy compacta y elegante, por lo que es reconocida como una de las ecuaciones más bellas de la Física.

Aquí, la “Ψ” representa la función de onda del electrón, una función de variable compleja que depende de la posición y el tiempo, “m” es la masa en reposo del electrón e “i” la unidad imaginaria. La ecuación aparece muy compacta, gracias a que el operador para derivada parcial ∂, atravesado por la barra, implica una sumatoria de derivadas parciales.
Principios aplicados en la Ecuación de Dirac
Paul Dirac (1902-1984) fue un físico teórico, ingeniero y matemático británico, que intentó con éxito unir dos teorías, en principio irreconciliables, en una forma magistral: la mecánica cuántica y la teoría de la relatividad. Antes de que Dirac diera con su famosa ecuación en 1928, estaba claro que el electrón a escala atómica tiene comportamiento dual y simultáneo de onda y de partícula.
Para describir matemáticamente el estado de un electrón, la mecánica cuántica postula una función matemática en variable compleja llamada la función de onda Ψ (letra griega “psi”), que depende de la posición y el tiempo.
Puede que el hecho de ser una función de variable compleja no aclare la situación, pero lo importante es que el valor absoluto al cuadrado de Ψ es la probabilidad de encontrar el electrón en determinada posición. Y es que, la mecánica cuántica, a diferencia de la mecánica clásica de Newton, es no-determinista. Aquí se habla de probabilidades, no certidumbres.
La función Ψ queda determinada por la ecuación de Schrodinger, la cual se obtiene partiendo de la fórmula de energía clásica (no-relativista) y aplicando las reglas de cuantización a la energía y momentum. De este modo se obtiene una ecuación diferencial para la función de onda.
Las soluciones de dicha ecuación, aplicadas al electrón único del átomo de hidrógeno, son los niveles de energía y los orbitales electrónicos. Pero esta teoría toma en cuenta la masa y la carga del electrón, más no una propiedad fundamental del mismo: el espín o momento angular intrínseco, por lo que Dirac resolvió tomar cartas en el asunto y aplicar estos principios.
1.- Las reglas de cuantización de Schrodinger
Dirac decidió mantener como primer principio las reglas de cuantización para la energía E y el momentum p, las cuales se expresan así:
\(E\to \text{i}\hbar \frac{\partial }{\partial \text{x}}\text{ }\!\!\psi\!\!\text{ }~\)
\(p\to \text{i}\hbar \frac{\partial }{\partial \text{x}}\text{ }\!\!\psi\!\!\text{ }\)
2.- La energía relativista
La energía relativista de una partícula de masa m en reposo, que se mueve con momentum p está dado por la ecuación más famosa de Einstein:
\(E=\sqrt{{{m}^{2}}{{c}^{4}}+{{p}^{2}}{{c}^{2}}}\)
En esta ecuación, c representa la velocidad de la luz, y de la misma se deduce que, incluso una partícula en reposo, con p = 0, tiene una energía igual al producto de su masa en reposo por la velocidad de la luz al cuadrado.
3.- Linealizar la ecuación de energía
La ecuación anterior es una ecuación no lineal, y al intentar aplica las reglas de cuantización, queda un operador diferencial dentro de una raíz cuadrada, algo muy difícil manejar matemáticamente.
Por lo tanto, Dirac se propuso linealizar dicha ecuación, con el uso de dos parámetros a determinar, a los que llamó α y β:
\(E=\alpha \cdot pc+\beta \cdot m{{c}^{2}}\)
4.- Buscar soluciones en una dimensionalidad mayor
Igualando la expresión anterior de la energía linealizada con la ecuación de energía de Einstein, es imposible conseguir soluciones para α y β, ni siquiera en el campo de los números complejos.
Por eso Dirac buscó soluciones con objetos matemáticos de dimensionalidad mayor, como las matrices. Exploró varias posibilidades: con matrices 2X2, con matrices 3X3 y por último con matrices 4X4, con las que finalmente consiguió una solución:
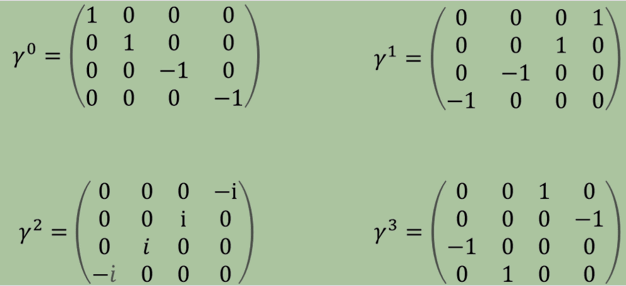
La matriz γ0 (se lee “gamma cero”) corresponde a la coordenada temporal y las demás, a las tres coordenadas espaciales.
5.- Aplicar reglas de cuantización sobre una función vectorial de cuatro dimensiones
Las reglas de cuantización conducen a operaciones con derivadas que normalmente actúan sobre una función de onda escalar, pero como las constantes α y β son matrices de 4X4, los operadores diferenciales actuarán sobre un vector de cuatro dimensiones Ψ, al que luego se le llamó el espinor.
Si se elige un sistema de medida en el que la velocidad de la luz sea 1, la ecuación de Dirac se escribe así:
\(\left( i{{\gamma }^{\mu }}\frac{\partial }{\partial {{\text{x}}^{\mu }}}-\text{m} \right)\text{ }\!\!\psi\!\!\text{ }=0\)
En la ecuación anterior se expresa una sumatoria sobre los índices μ, comenzando desde 0 hasta 3, y por supuesto, “i” es la unidad imaginaria, ya que se trata de una ecuación en variable compleja.
Esta ecuación se suele compactar más mediante el uso del símbolo ∂ atravesado por una barra inclinada / para simbolizar la sumatoria de derivadas, así queda como la ecuación mostrada en la figura que aparece al comienzo del artículo.
Las soluciones de la ecuación de Dirac y el espín del electrón
La ecuación de Dirac es una ecuación de autovalores que corresponden a las energías posibles. Hay dos soluciones con energía positiva, una para cada estado de espín, y dos soluciones con energía negativa, también para cada uno de los dos estados posibles de espín.
Es de resaltar que el espín, en la ecuación de Dirac, aparece naturalmente, como un resultado de sus posibles soluciones y a consecuencia directa de tomar en cuenta la energía relativista.
Es así que, por primera vez en la Física, se cae en cuenta que el espín, una propiedad intrínseca del electrón y de otras partículas elementales, es una consecuencia de la relatividad. Por cierto, esta propiedad del electrón había sido comprobada antes que Dirac formulara su ecuación, gracias al famoso experimento de Stern y Gerlach en 1922.
La ecuación de Dirac predice la existencia de la antimateria
Dirac fue increíblemente brillante al haber obtenido su ecuación, aplicando ingeniosamente las matemáticas, y también es notable la forma en que interpretó sus soluciones.
Al principio, a Dirac no le quedaba claro si había electrones con energía cinética negativa. Entonces teorizó lo siguiente:
El vacío (la ausencia de electrones) no es tal, sino que está lleno de electrones con energía negativa en sus dos estados de espín.
Lo que sucede es que los científicos no tienen la posibilidad de ver esos electrones, de la misma forma que normalmente no se ven los peces del mar, de allí sale la denominación mar de Dirac.
Ahora bien, si un fotón es capaz de entregar energía suficiente a uno de los electrones de ese mar, entonces sí será visible, apareciendo de la nada.
Pero el espacio vacante en el mar de Dirac es un hueco de carga positiva, es decir una partícula de la misma masa y carga que el electrón, pero positiva, llamada positrón.
Poco tiempo después de la interpretación de Dirac, en 1932, Carl D. Anderson detectó experimentalmente el positrón.
Hoy día la antimateria es cosa común en los aceleradores de partículas y en la ciencia ficción. También se crean pares de electrones y positrones en la atmósfera superior, debido a la radiación solar, pero rápidamente el positrón se aniquila con cualquier partícula de materia que encuentre a su paso.
No obstante, es posible contener antimateria en trampas magnéticas al vacío, para así evitar su contacto con la materia y su ulterior aniquilación.

Trabajo publicado en: Ago., 2021.