Significado de movimiento parabólico Definición, explicación, y ecuaciones

Licenciada en Física
Definición formal
El movimiento parabólico ocurre cuando el móvil describe una trayectoria con forma de parábola. Es una acción muy natural y fácil de observar, ya que ocurre cuando se lanza cualquier objeto formando ángulo menor de 90º con la horizontal y se le deja bajo la acción de la gravedad. De esta forma, por ejemplo, se mueve una pelota de béisbol luego de ser golpeada con el bate, o el balón de fútbol cuando se patea.
Observar que la trayectoria parabólica es una posibilidad real para el movimiento de los cuerpos celestes. Los planetas siguen trayectorias elípticas alrededor del Sol según las leyes de Kepler, pero se han encontrado algunos cometas que transitan una trayectoria parabólica y abierta. Por lo tanto, una vez que pasan por su máximo acercamiento al Sol, se alejan para nunca regresar.
Pero volviendo a los móviles cercanos a la superficie terrestre, los cuerpos que se proyectan o lanzan con ángulo respecto a la horizontal se ven obligados a volver al suelo a causa de la gravedad, que siempre es vertical y apunta hacia el centro de la Tierra. Este movimiento se describe fácilmente a través de movimientos estudiados previamente: el movimiento rectilíneo uniforme (MRU) y el movimiento rectilíneo uniformemente acelerado (MRUV).
Explicación del fenómeno físico
Para este análisis se omiten la resistencia del aire, los efectos de la rotación de la Tierra y su forma curva y además el proyectil se representa como un objeto puntual.
Al objeto móvil o proyectil, se le imprime una velocidad inicial vo, la cual forma un ángulo θ con la horizontal y se le deja luego a la acción de la gravedad g, que en todo momento está dirigida verticalmente hacia abajo y se considera constante. Estas cantidades son vectoriales y por eso se denotan con letra negrita en texto impreso.
El punto de lanzamiento es el origen del movimiento y el siguiente diagrama muestra la trayectoria parabólica y(x) que sigue el móvil. La velocidad es el vector tangente a cada punto de la curva.
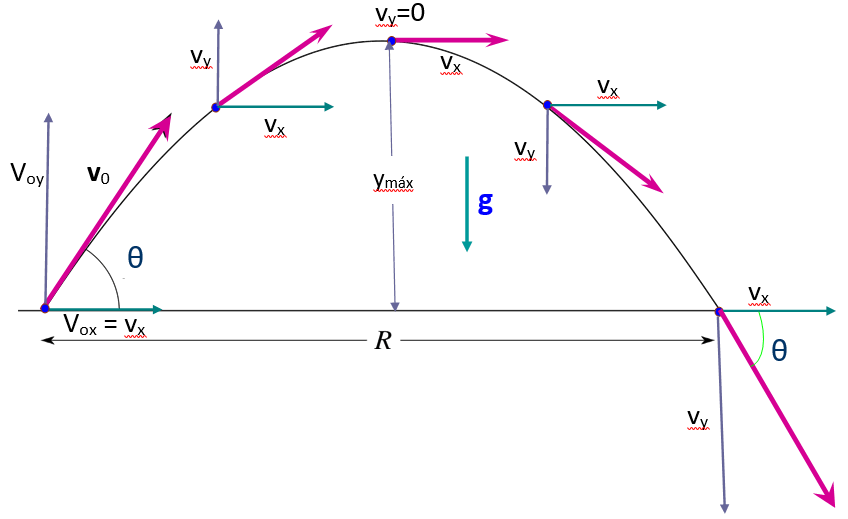
La figura muestra que la velocidad inicial vo se descompone en dos componentes: una horizontal vox y otra vertical voy, las cuales se relacionan a través del ángulo θ como sigue:
vox = vo∙cos θ
voy = vo∙sen θ
De esta forma, el movimiento parabólico se puede descomponer en dos movimientos simultáneos:
1) Uno horizontal con aceleración nula y velocidad constante de magnitud vx y
2) Otro vertical con velocidad inicial de magnitud voy y aceleración g dirigida verticalmente hacia abajo.
Se observa el vector velocidad v en varios puntos de la trayectoria del móvil y a medida que se eleva, la componente vertical de la velocidad vy va disminuyendo, hasta hacerse 0 en el punto más alto. No significa que el móvil se detiene ahí, ya que la velocidad horizontal vx es constante en todo momento, por eso se representa con una flecha cuya longitud siempre es la misma.
Una vez que el móvil sobrepasa la altura máxima, el sentido de la componente vertical de la velocidad se invierte, lo cual tiene sentido porque el móvil se está precipitando al suelo.
Cuando el proyectil se encuentra de bajada y pasa por la misma altura de la cual partió, el módulo de su velocidad es igual a vo, pero el ángulo que forma con la horizontal, que vuelve a ser θ, ahora está por debajo de ésta, indicando que la componente vertical de la velocidad invirtió su sentido.
Ecuaciones
Si se piensa en el movimiento parabólico del proyectil como la superposición de dos movimientos que ocurren simultáneamente, se tienen dos conjuntos de ecuaciones: uno para el MRU y otro para el MRUV.
El primero de estos movimientos ocurre siempre a lo largo del eje horizontal o eje x, mientras que el otro es vertical y dirigido a lo largo del eje y:
Ecuación de la posición para el movimiento horizontal
1) x (t) = x0 + vox∙t = x0 + (vocos θ)∙t
Donde t es el tiempo y x0 es la posición inicial del móvil, que se puede elegir como 0, simplificando a:
2) x (t) = vox∙t = (vocos θ)∙t
Ecuación de la posición para el movimiento vertical
Asignando al sentido de la gravedad el signo negativo, queda:
3) y (t) = y0 + voy ∙t − ½g∙t2 = y0 + (vosen θ)∙t − ½g∙t2
Escogiendo y0 = 0 resulta:
4) y (t) = voy∙t − ½g∙t2 = (vosen θ)∙t − ½g∙t2
Ecuación de la velocidad para el movimiento horizontal
La velocidad en el movimiento horizontal es constante:
5) vx = vox = vocos θ
Ecuaciones de la velocidad para el movimiento vertical
La velocidad inicial vertical es:
6) voy = vosenθ
La velocidad en función del tiempo para cualquier instante de tiempo es:
7) vy = voy − gt = (vo ∙senθ)− gt
La ecuación para la velocidad y la posición es:
8) vy2 = voy 2 − 2gy
Ecuación para la altura máxima
Al alcanzar la altura máxima, la velocidad vertical se anula momentáneamente antes de cambiar de sentido, por lo tanto, haciendo vy = 0 en la ecuación 8) y llamando ymax a la altura máxima se obtiene:
voy 2− 2g.ymáx = 0
Y despejando ymax queda:
9) \({{y}_{\max }}=\frac{\text{v}_{\text{oy}}^{\text{2}}}{\text{2g}}\)
10) \({{y}_{\max }}=\frac{{{\left( {{\text{v}}_{\text{o}}}sen\theta \right)}^{2}}}{\text{2g}}\)
Ecuación para el tiempo máximo
El tiempo que tarda el proyectil en alcanzar la altura máxima es el tiempo máximo tmáx. Se obtiene haciendo vy = 0 en la ecuación 7) y despejando:
vo .sen α − gtmáx = 0
11) \({{t}_{\max }}=\frac{{{\text{v}}_{\text{oy}}}}{\text{g}}\)
12) \({{t}_{\max }}=\frac{{{\text{v}}_{\text{o}}}sen\theta }{\text{g}}\)
Ecuación para el tiempo de vuelo
El tiempo de vuelto tv es el tiempo que tarda el proyectil en el aire. Para un lanzamiento a nivel, es decir, cuando el móvil parte del suelo y regresa a él cayendo más adelante, se tiene:
13) tv = 2tmax
Si el lanzamiento no es a nivel, el tiempo de vuelo puede calcularse a partir de la posición final o de la velocidad final, dependiendo de los datos que aporte el enunciado del problema.
Ecuación para el alcance máximo horizontal
El alcance máximo horizontal es la distancia horizontal máxima que recorre el proyectil, en la figura aparece denotada como R. Se calcula a partir de 1) o 2) cuando se conoce el tiempo de vuelo:
14) R = vox∙tv
Ecuación de la trayectoria
La ecuación de la trayectoria es la parábola y(x), que se obtiene eliminando el parámetro “t” de las ecuaciones 2) y 4). Luego de operar y simplificar, el resultado es:
15) \(\text{y}=\text{(tg}\theta \text{)x-}\left( \frac{\text{g}}{\text{2v}_{\text{o}}^{\text{2}}\cdot {{\cos }^{2}}\theta } \right){{x}^{2}}\)
Ejercitación
Desde el suelo se lanza una pelota con velocidad inicial de 12 m/s formando ángulo de 36º con la horizontal, cayendo más adelante al mismo nivel suelo. Despreciando los efectos del rozamiento, calcular:
a) El tiempo que demora en el aire
b) ¿Cuál fue la altura máxima alcanzada?
c) A qué distancia del punto de partida cayó la pelota.
Tomar g = 9.8 m/s2.
Respuesta a
La componente vertical de la velocidad incial se calcula a partir de 6):
voy = vosenθ = 12 m/s×sen 36º = 7.05 m/s
Luego se calcula el tiempo máximo con la ecuación 11):
\({{t}_{\max }}=\frac{{{\text{v}}_{\text{oy}}}}{\text{g}}=\frac{7.05}{9.8}s=0.72s\)
Como es un lanzamiento a nivel, el tiempo de vuelo es el doble del tiempo máximo:
tv = 2 × 0.72s = 1.44 s
Respuesta b
Sustituyendo valores en la ecuación 9):
\({{y}_{\max }}=\frac{\text{v}_{\text{oy}}^{\text{2}}}{\text{2g}}=\frac{{{\left( 7.05 \right)}^{2}}}{2\times 9.8}m=\text{2}\text{.5m}\)
Respuesta c
Se requiere la componente horizontal de la velocidad inicial y luego se utiliza la ecuación 14):
vox = vo ∙cosθ = 12 m/s × cos 36º = 9.7 m/s
R = vox∙tv = 9.7 m/s × 1.44 s ≈ 14.0 m
Quiere decir que la pelota cae a 14 m más adelante del punto de lanzamiento.

Trabajo publicado en: Ene., 2021.