Significado de dinámica del movimiento circular Definición, fórmulas, y ejercicios

Licenciada en Física
Definición formal
La dinámica del movimiento circular es el estudio de las fuerzas que lo originan, regido por la segunda ley de Newton, recordando que en todo movimiento circular existe una aceleración dirigida hacia el centro de la trayectoria: la aceleración centrípeta.
Innumerables objetos en el mundo real tienen este tipo de movimiento, desde las ruedas de los automóviles en marcha, pasando por las aspas de los electrodomésticos, hasta piezas de maquinaria diversa.
En cuanto al movimiento circular se distinguen dos clases:
i) Uniforme
ii) No uniforme
En el movimiento circular uniforme la rapidez se mantiene constante, mientras que en el movimiento circular no uniforme, esta puede variar. Seguidamente se describirá la dinámica en ambos casos, utilizando el modelo de partícula, es decir, el objeto en movimiento tiene masa, pero sus dimensiones no se toman en cuenta.
Fórmula de la dinámica del movimiento circular uniforme
Cuando un objeto se mueve sobre una circunferencia de radio R y su rapidez v es constante, el movimiento es circular uniforme. Sin embargo, se observa que el vector velocidad cambia continuamente de dirección. La magnitud responsable de este cambio es la aceleración centrípeta , cuyo módulo es:
\({{a}_{c}}=\frac{{{v}^{2}}}{R}\)
El módulo de la aceleración centrípeta se mantiene constante en el movimiento circular uniforme, ya que tanto v como R permanecen inalterados.
Seguidamente, aplicando la segunda ley de Newton, la cual asegura que un objeto de masa m con aceleración no nula experimenta una fuerza neta, resulta la ecuación:
\(\vec{F}=m{{\vec{a}}_{c}}\)
Designando al vector \(\hat{r}\)como el vector unitario en la dirección radial (hacia el centro de la circunferencia), la ecuación anterior se transforma en:
\(\vec{F}=m\frac{{{v}^{2}}}{R}\hat{r}\)
Nota: algunos autores toman la dirección radial hacia el centro de la circunferencia como el sentido negativo, en cuyo caso:
\(\vec{F}=m\frac{{{v}^{2}}}{R}(-\hat{r})\)
La fuerza en el movimiento circular uniforme, a veces llamada fuerza centrípeta, puede ser única o bien una combinación de varias fuerzas, con tal de que la fuerza neta o resultante esté dirigida hacia el centro de la trayectoria. No se trata de una nueva fuerza, más bien suelen ser fuerzas bien conocidas, como la gravedad, el rozamiento, la fuerza eléctrica, la tensión en una cuerda y más.
Si se conoce la velocidad angular del movimiento, denotada como ω, las ecuaciones anteriores se expresan del siguiente modo:
v = ω∙R
ac = ω2∙R
Fc= mω2∙R
Fórmula de la Dinámica del movimiento circular no uniforme
Está claro que en el movimiento circular siempre hay una aceleración centrípeta, asociada a la fuerza centrípeta (dirigida hacia el centro), que se ocupa de cambiar la dirección de la velocidad. Si además de un cambio de dirección hay un cambio en el módulo de la velocidad, esto es, la partícula acelera o frena, aparece una nueva componente de la aceleración, llamada aceleración tangencial.
En este movimiento, la fuerza neta no es totalmente radial, sino que tiene una componente radial y otra componente tangencial. La aceleración tangencial, denotada como at, se calcula mediante:
\({{a}_{t}}=\frac{dv}{dt}\)
Es decir, la derivada de la rapidez con respecto al tiempo. Con esto, el vector aceleración \(\vec{a}\)tiene dos componentes, la siempre presente aceleración centrípeta, que causa el cambio en la dirección de la velocidad y la aceleración tangencial, que se ocupa de cambiar la magnitud de la velocidad, quedando escrita como:
\(\vec{a}={{a}_{c}}\hat{r}+{{a}_{t}}\hat{\theta }\)
Donde el vector unitario \(\hat{\theta }\)representa la dirección tangencial a la circunferencia. El módulo de la aceleración viene dado por:
\(a=\sqrt{a_{c}^{2}+a_{t}^{2}}\)
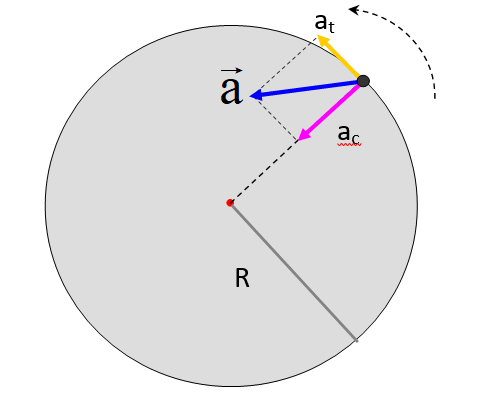
Nótese que la aceleración centrípeta ya no tiene magnitud constante, pues la rapidez de la partícula está variando.
Ejemplos de ejercicios resueltos
Ejemplo 1
Un niño de masa 25.0 kg se sienta a 1.10m del centro de un carrusel, el cual gira con movimiento circular uniforme a razón de 1.25 m/s. Hallar:
a) La aceleración centrípeta del niño.
b) La magnitud de la fuerza horizontal neta sobre el niño.
Respuestas
a) La aceleración centrípeta se calcula mediante la ecuación:
\({{a}_{c}}=\frac{{{v}^{2}}}{R}=\frac{{{\left( 1.25\frac{m}{s} \right)}^{2}}}{1.10m}=1.42\frac{m}{{{s}^{2}}}\)
b) La magnitud de la fuerza centrípeta viene dada por la segunda ley de Newton:
Fc = m∙ac = 25.0 kg × 1.42 m/s2 = 35.5 N.
Ejemplo 2
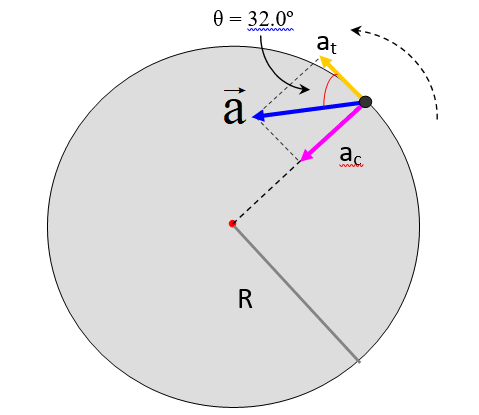
Una partícula tiene movimiento circular con radio igual a 2.90 m. En determinado instante, su aceleración tiene módulo igual a 1.05 m/s2, formando ángulo de 32.0º con la dirección del movimiento. Suponiendo que la aceleración tangencial es constante, determinar:
a) La rapidez de la partícula en ese instante
b) La rapidez cuando han transcurrido 2.00 segundos.
Respuesta
a) La dirección del movimiento es la dirección tangencial, por lo tanto el vector aceleración forma con esta un ángulos de 32.0º, como se indica en el diagrama. De esta manera, las componentes radial y tangencial de la aceleración son:
at = a∙cos 32.0º = 1.05 m/s2 ∙ cos 32.0º = 0.89 m/s2
ac = a∙sen 32.0º = 1.05 m/s2 ∙ sen 32.0º = 0.56 m/s2
Conociendo la aceleración centrípeta se despeja la rapidez en ese instante:
\({{a}_{c}}=\frac{{{v}^{2}}}{R}\Rightarrow v=\sqrt{{{a}_{c}}\cdot R}=\sqrt{0.56\frac{m}{{{s}^{2}}}\times 2.90m}=1.27\frac{m}{s}\)
b) Como la aceleración tangencial es constante, se puede aplicar la fórmula:
\(v={{v}_{o}}+{{a}_{t}}\cdot t\)
La velocidad incial se conoce, ya que se calculó en el paso anterior y el tiempo es 2.00 s, según el enunciado, por lo tanto:
v = 1.27 m/s + 0.89 m/s2 ∙ 2.00 s = 3.05 m/s.

Trabajo publicado en: Ene., 2021.