Significado de circunferencia Definición, elementos, ecuación canónica-general, y ejercicios

Licenciada en Física
Definición formal
La circunferencia es aquella que cumplen los puntos del plano de coordenadas (x,y) y que pertenecen a determinada circunferencia de radio R.
La condición para que un punto pertenezca a la circunferencia, es que su distancia a otro punto, llamado centro y denotado por C, sea igual a R. Cuando la circunferencia está centrada en el origen de coordenadas, que corresponde al punto (0,0), su ecuación toma la forma: \({{x}^{2}}+\text{ }{{y}^{2}}=\text{ }{{R}^{2}}\) .
Pero este es un caso particular, pues la circunferencia puede estar centrada en cualquier otro punto del plano. Cuando el centro C de la circunferencia se ubica en las coordenadas arbitrarias (h,k), entonces su ecuación es \({{\left( x-h \right)}^{2}}+\text{ }{{\left( y-k \right)}^{2}}=\text{ }{{R}^{2}}\). La misma se conoce como ecuación canónica, ordinaria o forma estándar de la circunferencia, dependiendo de la literatura de referencia.
Elementos presentes en la gráfica de la circunferencia de un círculo
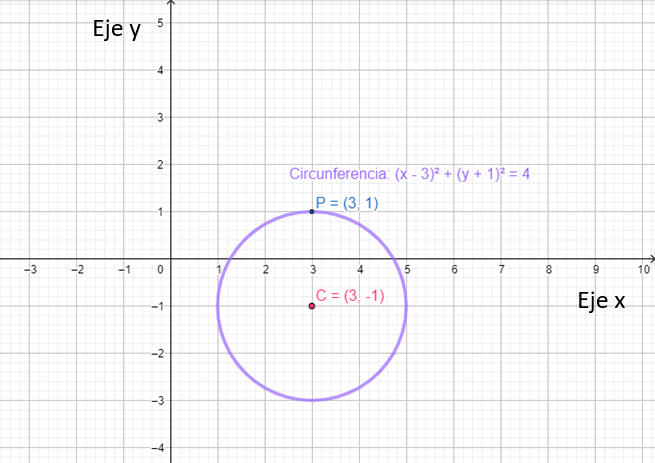
A modo de ejemplo, se tiene a continuación la gráfica de la circunferencia \({{\left( x-3 \right)}^{2}}+\text{ }{{\left( y+1 \right)}^{2}}=\text{ }4\). El centro de esta circunferencia es el punto C(3, −1) y en la gráfica aparece también el punto P (3,1), uno de los muchos que pertenece a esta circunferencia.
Es sencillo comprobar que P pertenece a esta circunferencia, pues al sustituir los valores en la ecuación, resulta una igualdad:
\({{\left( 3-3 \right)}^{2}}+\text{ }{{\left( 1+1 \right)}^{2}}=\text{ }4\)
\({{2}^{2}}=\text{ }4\)
Graficar a mano la circunferencia es un procedimiento muy sencillo, si se conocen el centro C y el radio R. Para ello se necesita papel milimetrado, lápiz, regla y compás, siguiendo este procedimiento:
– Sobre el papel milimetrado se marcan los ejes cartesianos y traza una escala.
– Después se marcan cuidadosamente el origen (0,0) y el centro (h,k) de la circunferencia.
– Por último, se apertura el compás al tamaño del radio, se coloca la punta en C y se traza la circunferencia de una sola pasada.
Ecuación Canónica a Ecuación General
Al desarrollar la ecuación canónica de la circunferencia mediante producto notable, se obtiene una expresión diferente para la ecuación, conocida como ecuación general de la circunferencia. Partiendo de:
\({{\left( x-h \right)}^{2}}+\text{ }{{\left( y-k \right)}^{2}}=\text{ }{{R}^{2}}\)
\({{x}^{2}}-\text{ }2xh\text{ }+\text{ }{{h}^{2}}+\text{ }{{y}^{2}}-\text{ }2yk\text{ }+\text{ }{{k}^{2}}=\text{ }{{R}^{2}}\)
Se ordena el resultado obtenido, reagrupando los términos:
\({{x}^{2}}+\text{ }{{y}^{2}}-\text{ }2xh-\text{ }2yk\text{ }+\text{ }\left( {{h}^{2}}~+\text{ }{{k}^{2}}-\text{ }{{R}^{2}} \right)\text{ }=\text{ }0\)
Y se le dan nuevos nombres a los coeficientes, así:
\(-\text{ }2h\text{ }=\text{ }D\)
\(-\text{ }2h\text{ }=\text{ }E\)
\({{h}^{2}}~+\text{ }{{k}^{2}}-\text{ }{{R}^{2}}=\text{ }F\)
Para obtener finalmente la ecuación general de la circunferencia:
\({{x}^{2}}+\text{ }{{y}^{2}}+\text{ }Dx\text{ }+\text{ }Ey\text{ }+\text{ }F\text{ }=\text{ }0\)
En conclusión, pasar de la ecuación canónica a la ecuación general es muy sencillo, únicamente requiere desarrollar los productos notables y reagrupar los términos. Y si se quiere pasar de la ecuación general a la forma canónica, se requiere del procedimiento inverso, llamado completar cuadrados. La explicación está en el ejercicio resuelto 2.
Ejercicios prácticos resueltos
Ejercicio 1: Hallar la ecuación canónica y la ecuación general de la circunferencia con radio R = 4 y centro C (5,-1). Dibujar también su gráfica.
Respuestas
Dado que las coordenadas del centro son (5,-1) entonces:
h = 5
k = -1
Por otro lado, el radio es R = 4. Sustituyendo todo en la ecuación canónica se obtiene:
\({{\left( x-5 \right)}^{2}}+\text{ }{{\left[ y\text{ }-\text{ }\left( -1 \right) \right]}^{2}}=\text{ }{{4}^{2}}\)
\({{\left( x-5 \right)}^{2}}+\text{ }{{\left( y\text{ }+1 \right)}^{2}}=\text{ }16\)
La ecuación general se obtiene desarrollando los productos notables y reacomodando los términos:
\({{x}^{2}}-\text{ }10x\text{ }+\text{ }25\text{ }+\text{ }{{y}^{2}}+\text{ }2y\text{ }+\text{ }1\text{ }=\text{ }16\)
\({{x}^{2}}+\text{ }{{y}^{2}}-\text{ }10x~+\text{ }2y\text{ }+\text{ }25+\text{ }1\text{ }-\text{ }16\text{ }=\text{ }0\)
\({{x}^{2}}+\text{ }{{y}^{2}}-\text{ }10x~+\text{ }2y\text{ }+\text{ }10\text{ }=\text{ }0\)
La gráfica de la circunferencia es:
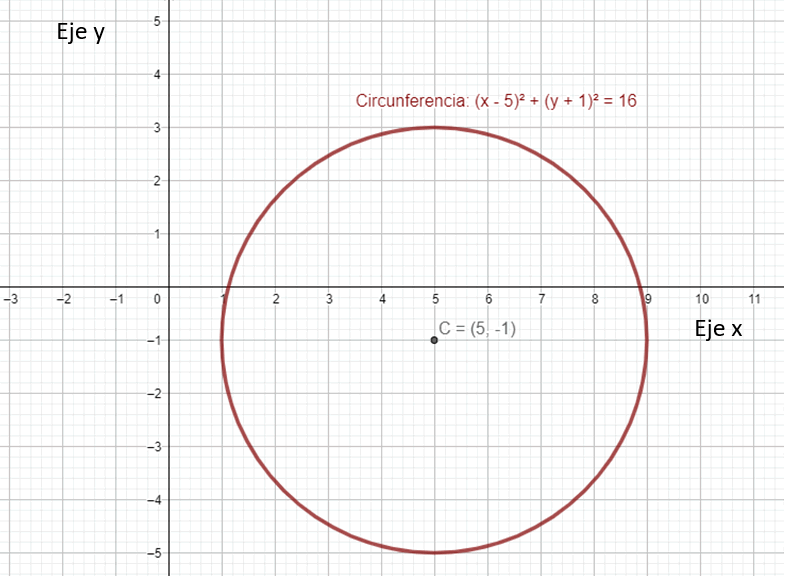
Ejercicio 2 Encontrar el centro y el radio de la siguiente circunferencia dada en forma general:
\({{x}^{2}}+\text{ }{{y}^{2}}-\text{ }4x~-\text{ }6y\text{ }-\text{ }12\text{ }=\text{ }0\)
Respuesta
Hay que llevar la ecuación general a la forma canónica mediante el método de completar cuadrados, cuyos pasos se muestran seguidamente:
Paso 1
Reacomodar los términos:
\(\left( {{x}^{2}}-\text{ }4x \right)~~+~\left( {{y}^{2}}-\text{ }6y \right)~=\text{ }-\text{ }12\)
Paso 2
Buscar números que transformen cada una de las expresiones entre paréntesis en trinomios cuadrados perfectos. Por ejemplo el paréntesis (x2 − 4x) se transformaría en un trinomio cuadrado perfecto si se le agregara un 4, ya que:
\({{x}^{2}}-\text{ }4x\text{ }+\text{ }4\text{ }=\text{ }{{\left( x-2 \right)}^{2}}\)
Claro que no se puede agregar a la expresión original un 4 así no más, ya que se altera, pero se puede agregar y al mismo tiempo se puede restar, entonces el original quedaría reescrito de una forma equivalente, sin alteración:
x2 − 4x = (x2 − 4x + 4) – 4 = (x−2)2 – 4
Se dice que se han completado los cuadrados en x. El procedimiento se repite para y:
\({{y}^{2}}-\text{ }6y\text{ }=\text{ }\left( {{y}^{2}}-\text{ }6y\text{ }+9 \right)\text{ }-\text{ }9\text{ }=\text{ }{{\left( y-3 \right)}^{2}}-\text{ }9\)
Completados los cuadrados en la variable y, la ecuación de la circunferencia, escrita en forma general, se transforma en:
(x−2)2 – 4+ (y−3)2 − 9 = − 12
Paso 3
Trasponer los términos independientes, llevándolos a la derecha de la igualdad, con esto se obtiene el radio de la circunferencia:
\({{\left( x-2 \right)}^{2}}+\text{ }{{\left( y-3 \right)}^{2}}~~=\text{ }-\text{ }12\text{ }+\text{ }9\text{ }+\text{ }4\text{ }=\text{ }1\)
Por lo tanto, la ecuación de la circunferencia buscada es:
\({{\left( x-2 \right)}^{2}}+\text{ }{{\left( y-3 \right)}^{2}}=\text{ }1\)
El centro es C (2,3) y el radio es R = 1. Se puede comprobar que esta expresión es equivalente a la expresión original si se desarrollan los productos notables y se simplifica. La gráfica de la circunferencia es:

Trabajo publicado en: Nov., 2020.