Significado de radián Definición, ejemplos, y conversión a grados

Licenciada en Física
Definición formal
El radián es parámetro de medición aplicable en ángulos planos, en cuya definición interviene el ángulo central, aquel que tiene su vértice en el centro de una circunferencia y sus lados del tamaño del radio de la misma.
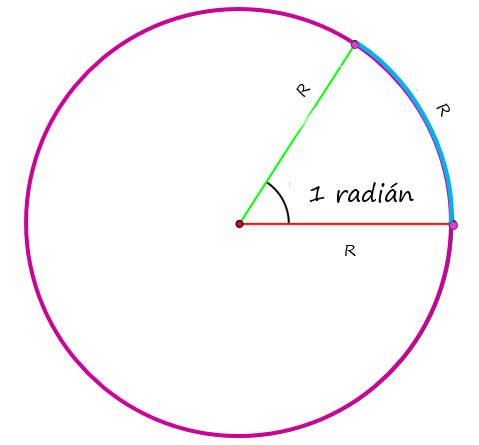
El ángulo que subtiende un arco de igual longitud que el radio de la circunferencia, mide exactamente 1 radián, tal como se muestra en la figura.
La longitud del arco azul es R, la misma que el radio de la circunferencia, así como los lados del ángulo.
Este sistema de medida se denomina sistema circular. El radián es, asimismo, la manera de medir ángulos según el Sistema Internacional de Unidades, SI, como unidad derivada. Se trata de una manera muy conveniente de expresar un ángulo, ya que de esta manera quedan escritos en términos del número π, como se verá más adelante.
¿Cuántos radianes hay en la circunferencia?
Dado que la longitud de la circunferencia es C = 2πR, significa que un radio está contenido 2π veces en dicha longitud. De allí que el ángulo subtendido por la circunferencia completa sea 2π radianes, que es aproximadamente 6.28 radianes.
Entonces, el ángulo llano, cuya medida en grados es 180º, equivale a π radianes, y el ángulo recto, que mide 90º, es π/2.
Otros ángulos notables son:
• 45º = π/4
• 60º = π/3
• 30º = π/6
En general, cualquier ángulo medido en grados sexagesimales se expresa en radianes mediante un factor de conversión, cuyo uso se muestra seguidamente.
Ejemplos de conversión de medidas angulares: grados a radianes y viceversa
En el sistema sexagesimal la circunferencia está dividida en 360 partes iguales, llamadas grados. Entonces la equivalencia entre grados sexagesimales y radianes es:
360º = 2π radianes
El radián no es una unidad, en el sentido en que lo son el metro, el segundo, el newton y muchas más. Algunos autores incluso prefieren no añadir la palabra “radián” al final de la medida del ángulo, ya que las medidas de los ángulos se consideran adimensionales.
Puesto que el ángulo llano de 180º equivale a π rad, o simplemente π, esto permite convertir la medida de un ángulo de un sistema al otro siguiendo esta breve instrucción:
• Se establece la conversión de grados a radianes al multiplicar el valor del ángulo dado por π /180º.
• De igual manera, para convertir radianes a grados, se multiplica el ángulo dado por 180º/ π.
Ejemplos de casos
a) Expresar en grados sexagesimales el ángulo cuya medida en radianes es 6 π/5:
\(\frac{6\pi }{5}\times \frac{180{}^\text{o}}{\pi }=216{}^\text{o}\)
b) Expresar en radianes el ángulo dado por 342º:
\(342{}^\text{o}\times \frac{\pi }{180{}^\text{o}}=\frac{19\pi }{10}\)
Ángulo central
La medida vista en radianes al respecto de un ángulo central cualquiera θ está dada por la fórmula
\(\theta =\frac{s}{R}\)
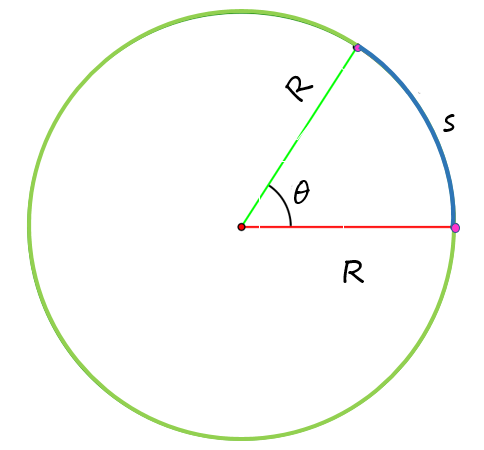
Donde s se identifica como el arco que subtiende el ángulo θ, y R es el radio de la circunferencia. Conociendo los valores de θ y R, se determina fácilmente el de s, lo cual conduce a algunas aplicaciones interesantes, como la del siguiente ejemplo:
Ejemplo de aplicación
Dos ciudades A y B, ubicadas sobre el mismo meridiano de la superficie terrestre, están respectivamente a 30º y 35º de latitud norte. Suponiendo que la Tierra es una esfera perfecta y que su radio es R = 6370 km, la distancia que las separa se puede encontrar a través de la definición de ángulo central.
De acuerdo a la siguiente figura, la distancia angular entre ambas ciudades es 35º − 30º = 5º.
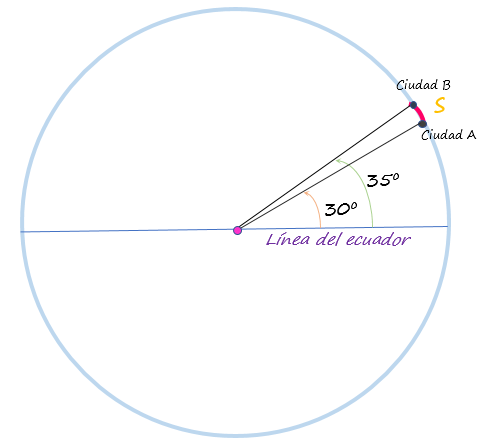
Como la fórmula del ángulo central es válida solo si se expresa en radianes, lo primero es aplicar el factor de conversión visto en las secciones precedentes:
\(5{}^\text{o}\times \frac{\pi }{180{}^\text{o}}=\frac{\pi }{36}\)
Despejando s de la fórmula del ángulo central, que es la longitud del arco subtendido y equivale a la distancia buscada, se tiene:
s = R∙θ = 6370 km × (π/36) = 555.9 km
Se concluye que las ciudades A y B distan 555.9 km.
¿De dónde surge el radián?
Se le atribuye el descubrimiento del radián al matemático y astrónomo inglés Roger Cotes (1682-1716), cercano colaborador de Isaac Newton, si bien Cotes nunca lo llamó de esta manera. El término que solía emplearse era el de “circular measure”, o medida circular del ángulo, lo cual es obvio, dado que se empleó el ángulo central de una circunferencia para definir al radián.
Los primeros en emplear el nombre de radián, derivado del inglés “radial angle”, fueron el ingeniero irlandés James Thomson (1822-1892), hermano mayor del físico William Thomson, Lord Kelvin y el matemático escocés Thomas Muir (1844-1934). Con el tiempo, la denominación de “radián” finalmente se extendió en la mayoría de los textos de matemática y física.

Trabajo publicado en: Jun., 2021.