Significado de Efecto Compton Definición, principios, y ecuaciones

Licenciado en Física
El Efecto Compton es un fenómeno cuántico que ocurre cuando un fotón incidente dirigido a un átomo choca con uno de sus electrones libres y le cede parte de su energía. El resultado de esta interacción es la dispersión del fotón incidente y el aumento en su longitud de onda (o disminución de su frecuencia).
El Efecto Compton fue observado por primera vez en 1920 por J. A. Franklin utilizando Rayos – X incidentes a una muestra. No obstante, la primera explicación teórica y cuantitativa del fenómeno fue dada por Arthur Compton en 1922 utilizando las dos grandes revoluciones de la Física del Siglo XX: La Teoría Corpuscular de la Luz brindada por Max Planck y el Efecto Fotoeléctrico descrito por Einstein, así como la Teoría de la Relatividad de este último. El Efecto Compton fue una de las primeras evidencias experimentales de la naturaleza corpuscular de la luz y del comportamiento cuántico de la materia.
Principios y ecuaciones del Efecto Compton
Cuando Compton se embarcó a explicar este fenómeno hizo dos suposiciones basándose en lo conocido hasta el momento. Primero supuso que la radiación electromagnética incidente podía ser descrita como pequeñas partículas sin masa llamadas “fotones”, tal y como lo habían manejado Planck y Einstein en sus investigaciones. Y, por último, asumió que podía describir el fenómeno si trataba a la interacción entre el fotón y el electrón como una colisión elástica entre ellos, de tal manera que tanto el momento lineal como la energía cinética se conservaban.
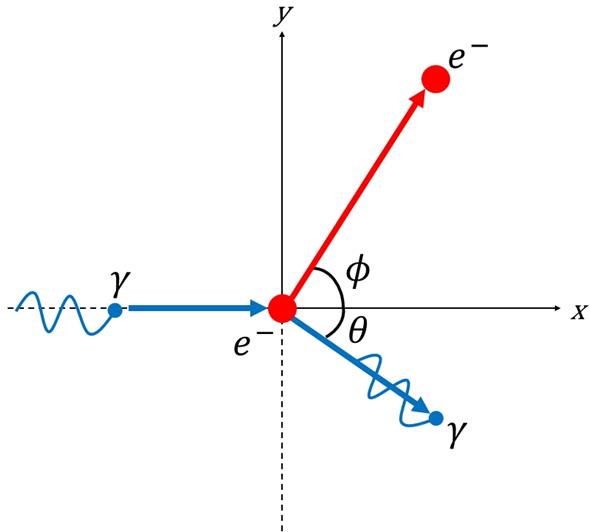
Podemos tratar esta situación considerando que inicialmente tenemos un fotón moviéndose en línea recta sobre el eje x y que colisiona elásticamente con un electrón que se encuentra en reposo. Después de la colisión, el electrón se dispersa con un ángulo \(\phi\) con respecto a la horizontal y el fotón se dispersa en un ángulo \(\theta\) también con respecto a la horizontal, tal y como podemos observar en la imagen superior. Para obtener la relación entre las longitudes de onda del fotón y su ángulo de dispersión basta con aplicar las leyes de conservación a esta colisión.
En este caso vamos a utilizar el momento y la energía de un fotón según la teoría corpuscular y la forma de la energía total para una partícula con masa según la relatividad. El fotón tendrá un momento inicial igual a \(h\nu/c\), donde h es la constante de Planck, \(\nu\) es su frecuencia y c es la velocidad de la luz. Tras la colisión el momento total en el eje x será la componente horizontal del momento p del electrón y la componente horizontal del momento \(h\nu\prime/c\) del fotón, donde \(\nu\prime\) es la frecuencia del fotón después de ser dispersado. Por lo tanto, la conservación del momento lineal en el eje x nos dice que:
\(\frac{h\nu}{c}=\frac{h\nu\prime}{c}\cos{\theta-p\cos{\phi}}\)
Por otro lado, en el eje y inicialmente no tenemos momento lineal, no obstante, después de la colisión se tiene la componente vertical del momento p del electrón y la componente vertical del momento \(h\nu^\prime/c\) del fotón, esto implica que:
\(p\sin{\phi-}\frac{h\nu\prime}{c}\sin{\theta}=0\)
Finalmente, tenemos que considerar la conservación de la energía cinética. El fotón tiene una energía inicial igual a \(h\nu\), mientras que, después de la colisión tendrá una energía \(h\nu^\prime\). Por su parte, según la cinemática relativista, la energía total de una partícula masiva en movimiento está dada por:
\(E=\sqrt{\left(pc\right)^2+\left(mc^2\right)^2}\)
Donde en este caso m sería la masa del electrón. La energía cinética del electrón será entonces su energía total menos su energía de reposo que está dado por \(E_r=mc^2\). En conclusión, la conservación de la energía cinética en esta colisión nos lleva a decir que:
\(h\nu=h\nu^\prime+\sqrt{\left(pc\right)^2+\left(mc^2\right)^2}-mc^2\)
Podemos reacomodar las expresiones obtenidas para la conservación del momento lineal y de la energía cinética para tener el siguiente sistema de ecuaciones:
\(h\nu-h\nu\prime\cos{\theta}=pc\cos{\phi}\)
\(h\nu\prime\sin{\theta}=pc\sin{\phi}\)
\(h\left(\nu-\nu^\prime\right)+mc^2=\sqrt{\left(pc\right)^2+\left(mc^2\right)^2}\)
Ahora sólo queda trabajar con estas tres ecuaciones para obtener una expresión que nos explique el fenómeno. Lo que podemos hacer primero es elevar al cuadrado las primeras dos ecuaciones y sumarlas, lo cual no da:
\(h^2\nu^2-2h^2\nu\nu\prime\cos{\theta+h^2\nu^{\prime2}(\cos^2{\theta+\sin^2{\theta}}})=p^2c^2(\cos^2{\phi}+\sin^2{\phi})\)
Para cualquier ángulo \(\alpha\) se cumple que \(\cos^2{\alpha}+\sin^2{\alpha}=1\), por lo tanto, la ecuación anterior se puede reducir a:
\(h^2\nu^2-2h^2\nu\nu\prime\cos{\theta}+h^2\nu^{\prime2}=p^2c^2\)
Podemos también elevar al cuadrado la tercera ecuación lo cual nos lleva a:
\(h^2\left(\nu-\nu^\prime\right)^2+2h\left(\nu-\nu^\prime\right)mc^2+\left(mc^2\right)^2=\left(pc\right)^2+\left(mc^2\right)^2\)
Si eliminamos el término común en ambos lados de la ecuación obtenemos que:
\(h^2\left(\nu-\nu^\prime\right)^2+2h\left(\nu-\nu^\prime\right)mc^2=p^2c^2\)
Como podemos darnos cuenta, en ambos procedimientos hemos obtenido dos expresiones que son iguales al término \(p^2c^2\), de esta manera no queda más que afirmar que los lados izquierdos de ambas ecuaciones deben de ser iguales entre sí, es decir que:
\(h^2\nu^2-2h^2\nu\nu\prime\cos{\theta}+h^2\nu^{\prime2}=h^2\left(\nu-\nu^\prime\right)^2+2h\left(\nu-\nu^\prime\right)mc^2\)
Desarrollamos el binomio al cuadrado que se encuentra en la parte derecha de la ecuación para obtener:
\(h^2\nu^2-2h^2\nu\nu\prime\cos{\theta}+h^2\nu^{\prime2}=h^2\nu^2-2h^2\nu\nu^\prime+h^2\nu^{\prime2}+2h\left(\nu-\nu^\prime\right)mc^2\)
Deshaciéndonos de los términos iguales en ambos lados y factorizando aquellos que son semejantes se tiene que:
\(h\nu\nu^\prime\left(1-\cos{\theta}\right)=\left(\nu-\nu^\prime\right)mc^2\)
Para obtener una expresión en términos de las longitudes de onda basta con reemplazar las frecuencias en términos de las longitudes de onda tales que \(\nu=c/\lambda:, \nu^\prime=c/\lambda\prime\). Donde \(\lambda\) y \(\lambda\prime\) son las longitudes de onda del fotón antes y después de colisión, respectivamente. Haciendo estas sustituciones y reacomodando algunos términos de la ecuación anterior obtenemos finalmente que:
\(\lambda^\prime-\lambda=\frac{h}{mc}(1-\cos{\theta})\)
O bien, dicho de otra manera:
\(\lambda^\prime=\lambda+\frac{h}{mc}(1-\cos{\theta})\)
Con esta expresión podemos darnos cuenta de varias cosas. Primero que nada, nos percatamos que la longitud de onda del fotón tras ser dispersado depende únicamente del ángulo de dispersión \(\theta\). Además, la longitud de onda \(\lambda\prime\) es siempre mayor o igual a la longitud de onda inicial \(\lambda\).
Tenemos que el valor mínimo de \(\lambda\prime\), al cual denotaremos como \(\lambda_{min}^\prime\), ocurre cuando \theta=0, es decir, cuando el fotón incidente no es dispersado y no pierde energía. En esta situación:
\(\lambda_{min}^\prime=\lambda\)
Por otro lado, el valor máximo \(\lambda_{max}^\prime\) ocurre cuando \(\theta=\pi=180°\), esto es cuando el fotón rebota horizontalmente, pero en dirección contraria a su dirección inicial. En este caso el fotón trasfiere la mayor cantidad de energía al electrón con el que colisiona, lo cual se refleja en una máxima disminución en la longitud de onda. Tenemos entonces que:
\(\lambda_{max}^\prime=\lambda+\frac{2h}{mc}\)
El Efecto Compton representó una de las piedras angulares de la teoría cuántica y de la estructura atómica de la materia. Hoy en día es fundamental en experimentos de difracción con Rayos X, en el estudio de la estructura cristalina de los sólidos y en las Tomografías Computarizadas.

Trabajo publicado en: Dic., 2023.
Referencias
John D. McGervey. (1983). Introduction to Modern Physics. United States: Academic Press.Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.