Significado de efecto doppler Definición, elementos y ecuaciones

Licenciada en Física
Definición formal
El efecto doppler es un fenómeno natural que está asociado a las ondas, muy fácilmente perceptible en las del sonido, entendiendo el cambio en la frecuencia que escucha el oyente, con respecto a la frecuencia real del emisor, cuando uno de los dos está en movimiento o simplemente existe un movimiento relativo entre ambos: fuente y receptor.
El ejemplo típico, reflejado en la imagen que acompaña estas líneas, plantea una persona que está en una calle concurrida, en la que muchos automóviles se encuentran circulando de un lado hacia otro. Así, cuando un vehículo que se acerca a la persona hace sonar su bocina, esta escucha un tono más agudo primero, y a medida que el automóvil se aleja, el tono se hace más bajo. Como el tono depende de la frecuencia, esto significa que si la fuente (el vehículo) se mueve respecto al receptor, la onda sonora experimenta un aparente cambio en dicha frecuencia, al menos en lo que respecta a quien escucha.
Este efecto aparece también en las ondas luminosas, pero a las personas les cuesta más notarlo en ese caso. En cambio, sí que es muy evidente cuando pasa cerca velozmente una ambulancia sonando la sirena o una locomotora con el silbato a todo volumen.
¿Qué caracteriza a una onda?
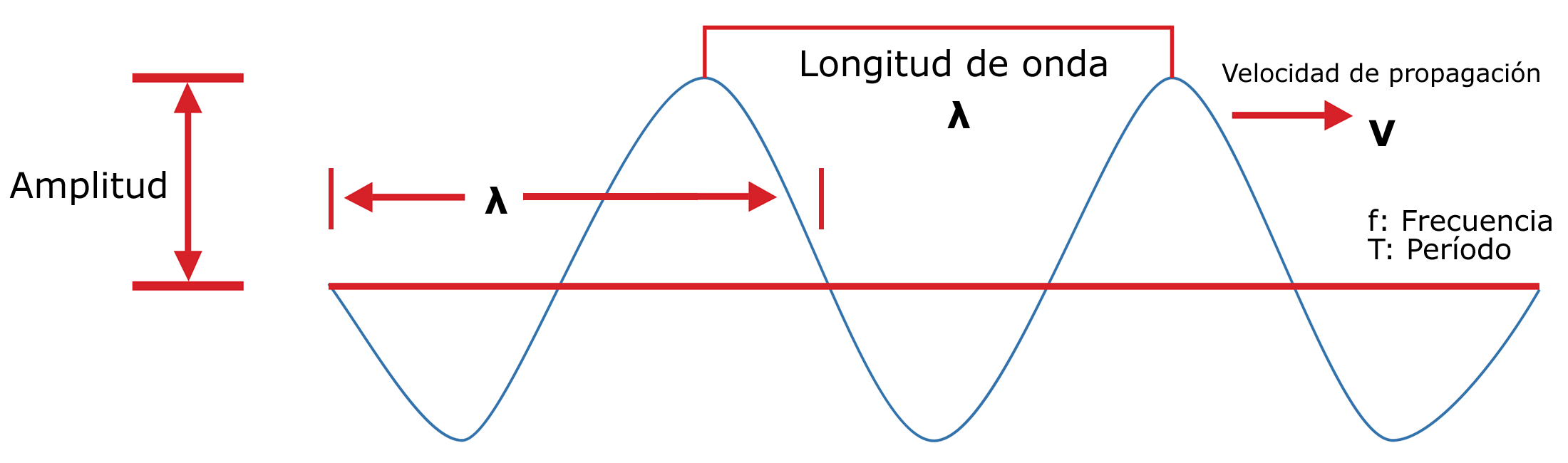
Para comprender el efecto Doppler hay que conocer primero un poco acerca de las ondas. Estas perturbaciones que se mueven en un medio material o en el vacío, se caracterizan por tener frecuencia f, período T, amplitud A y longitud de onda λ. El período es el tiempo que tarda en repetirse un ciclo completo y la frecuencia es el inverso del período. La amplitud es la altura máxima alcanzada por la cresta de la onda y la longitud de onda es la distancia que separa dos crestas.
La relación entre longitud de onda y frecuencia es a través de la velocidad de la onda v:
v = λ.f.
Como la frecuencia es el inverso del período, ocurre que:
\(f=\frac{1}{T}\)
La frecuencia de la onda determina cuándo aparece una cresta: si la frecuencia es muy alta, las crestas aparecen rápidamente una tras otras. Y cuando la frecuencia es baja, las crestas están más espaciadas.
Por su parte, la velocidad de la onda relaciona a la distancia que recorre la perturbación en un intervalo de tiempo dado.
Si se trata de una onda sonora en un medio material como el aire, su velocidad es de 340 m/s, aproximadamente constante. Y el tono del sonido dependerá precisamente de su frecuencia: los sonidos agudos tienen elevada frecuencia (menor longitud de onda) y los sonidos graves son de baja frecuencia (gran longitud de onda).
La onda puede representarse mediante una gráfica como la siguiente, ya que es un fenómeno cíclico o repetitivo:
Elementos que formulan el efecto Doppler
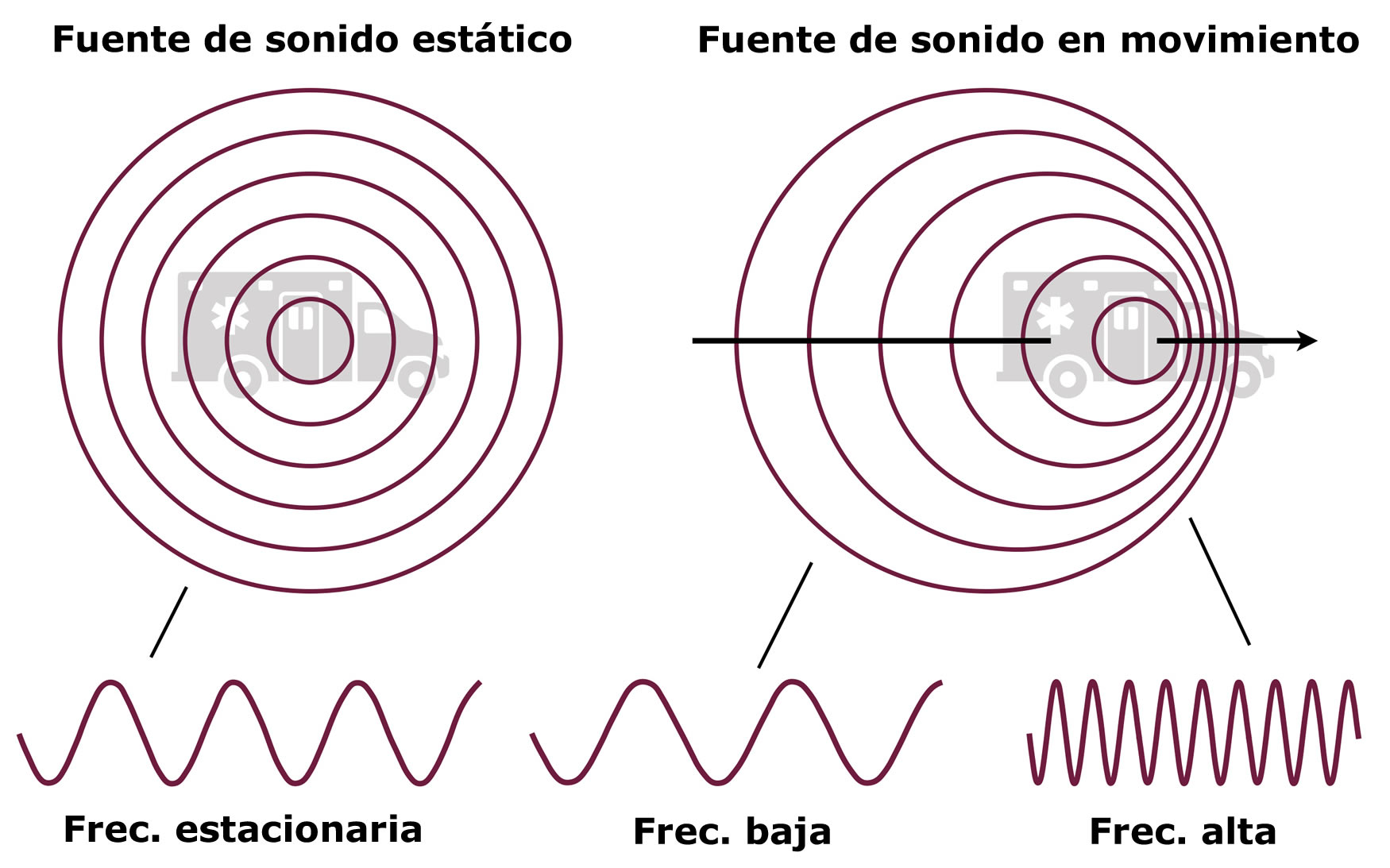
Supóngase una fuente de sonido estacionaria, que emite ondas sonoras en todas las direcciones, cuyos frentes de onda (los lugares donde la presión del aire es máxima) se representan en la siguiente figura mediante circunferencias. La separación entre ellas es la longitud de onda. Si tanto la fuente como el receptor permanecen quietos, este recibe en su oído la misma frecuencia que emite la fuente y no hay problema.
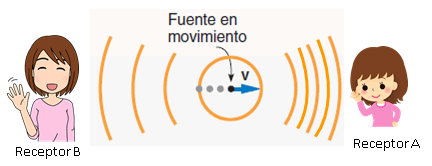
Pero cuando la fuente se mueve hacia el oyente, quien permanece fijo en su posición, los frentes de onda parece que se juntan porque la fuente se ha desplazado una cierta distancia hacia la persona.
Así la distancia entre las crestas se ha reducido. Pero como esta distancia representa la longitud de onda λ y se sabe que la velocidad del sonido en el aire es constante, la frecuencia f se hace más grande para que el producto v = λ.f se mantenga sin cambios.
Mientras más rápido se mueve la fuente hacia el receptor, más se amontonan los frentes de onda uno delante del otro, y la reducción de la longitud de onda, con el consiguiente aumento de la frecuencia es más notoria.
Por el contrario, para un observador del cual se aleja la fuente móvil, ocurre que los frentes de onda se distancian más entre sí. Y al aumentar la longitud de onda, la frecuencia detectada es menor.
Ecuaciones del Efecto Doppler: emisor móvil y receptor fijo
Para cuantificar el efecto Doppler en las ondas sonoras cuando la fuente viaja hacia el receptor, se toman en cuenta los siguientes parámetros:
– v: velocidad del sonido en el aire
– fo: frecuencia de la fuente sonora
– vF: la velocidad de la fuente
– f: frecuencia que escucha el receptor
– To: período de la fuente sonora
La fuente F recorre una distancia dF en un tiempo To dada por dF = vF ∙To, mientras que el frente de onda recorre d = v∙To. La longitud de la onda que llega hasta el receptor se llama longitud de onda efectiva y se denota como λef.
Para el receptor A, hacia el cual se dirige la fuente móvil, λef es la diferencia entre estas distancias:
λef = v∙To – vF ∙To
Por lo tanto la frecuencia que escucha A es:
\(f=\frac{v}{{{\lambda }_{ef}}}=\frac{v}{\left( v-{{v}_{F}} \right){{T}_{o}}}\)
Y como v = λ.f y la frecuencia es el inverso del período, la ecuación anterior se reescribe como:
\(f=\frac{v}{{{\lambda }_{ef}}}=\frac{v}{\left( v-{{v}_{F}} \right)}{{f}_{o}}\)
¿Y cuál es la frecuencia que percibe el oyente que está detrás de la fuente, el receptor B? Pues ya que la longitud de onda se estira porque la fuente se aleja, resulta una frecuencia menor:
\(f=\frac{v}{{{\lambda }_{ef}}}=\frac{v}{\left( v+{{v}_{F}} \right)}{{f}_{o}}\)
El efecto Doppler también se presenta si la fuente está quieta y es el oyente quien se aproxima a ella, o si hay movimiento relativo entre ambas. Cuando es el observador quien se dirige a la fuente, intercepta las crestas de los frentes de onda más rápido, por lo tanto oye una frecuencia mayor (sonido más agudo) que la frecuencia real. Ocurre lo contrario si el observador se aleja de la fuente.
Descubrimiento del efecto Doppler
El efecto Doppler del sonido es conocido desde tiempos inmemoriales, pero fue Christian Doppler (1803-1853), un físico y matemático austríaco, quien pasó a la historia como el primero en explicarlo en 1842, por eso se le llamó así en su honor, aunque él no lo investigó con las ondas sonoras, sino con la luz de las estrellas binarias.
Doppler razonó acertadamente que en realidad la fuente no cambia su frecuencia, sino que algo relacionado con el movimiento, determina que el receptor la perciba diferente a como realmente es.
Otro científico, el holandés Christoph Buys Ballot (1817-1890) comprobó, poco tiempo después de publicado el trabajo de Doppler, este aparente cambio en la manera de percibir el sonido, pidiendo a un conjunto de músicos que tocara una nota musical subidos a un tren que iba y venía, mientras los oyentes en el andén registraban los cambios que escuchaban en la nota.

Trabajo publicado en: Nov., 2020.
Ilustraciones: Dimitrios, Mrhighsky